Pokec (957) 
Chat řešitelů a organizátorů Matematického korespondenčního semináře. Dotazy týkající se úloh z aktuálních sérií směřujte na e-mail info (zavináč) prase.cz.
Zdeněk Pezlar | org | 8. 1. 2025 12:56:11Čau,
chtěl(a) bys trochu potrénovat mozkové závity přes blížícím se krajským kolem Matematické olympiády A? Potom je tu právě pro tebe speciální TRiKSko -- tréninková soutěž semináře iKS. Stačí si najít 4 hodiny času :)
Bližší informace najdeš na https://iksko.org/triks/current.php.
chtěl(a) bys trochu potrénovat mozkové závity přes blížícím se krajským kolem Matematické olympiády A? Potom je tu právě pro tebe speciální TRiKSko -- tréninková soutěž semináře iKS. Stačí si najít 4 hodiny času :)
Bližší informace najdeš na https://iksko.org/triks/current.php.
Matematická sekce (728) 
Tady se můžete zeptat na cokoliv, co se týká matematiky.
Johana Kubatová | org | 29. 5. 2025 10:38:28Ahoj! Určitě už se nemůžeš dočkat poslední várky hintů letošní série :)
Úloha 1
(a)+ skrytý text
(b)+ skrytý text
Úloha 2
(a)+ skrytý text
(b)+ skrytý text
Úloha 3
(a)+ skrytý text
(b)+ skrytý text
Úloha 4
(a)+ skrytý text
(b)+ skrytý text
Úloha 5
(a)+ skrytý text
(b)+ skrytý text
Úloha 6
(a)+ skrytý text
(b)+ skrytý text
Úloha 7
(a)+ skrytý text
(b)+ skrytý text
Úloha 1
(a)+ skrytý text
Rozepiš to a najdi dělitelnost osmi.
(b)+ skrytý text
Parita.
Úloha 2
(a)+ skrytý text
Mnohostěny nemusí být všechny stejného typu.+ skrytý text
Čtyřstěn a osmistěn.
(b)+ skrytý text
Pomocí obsahů stěn spočítej různými způsoby objem čtyřstěnu.+ skrytý text
CS.
Úloha 3
(a)+ skrytý text
Podívej se na součet čísel na tabuli.
(b)+ skrytý text
Podívej se na součet čtverců čísel na tabuli.
Úloha 4
(a)+ skrytý text
Sleduj počet levých bot v posouvajícím se úseku 10 bot.
(b)+ skrytý text
Nejprve vyřeš problém pro cykly.
Úloha 5
(a)+ skrytý text
Vyjádři si rovnost  pro několik různých
pro několik různých  . Dokážeš z toho něco vyvodit pro
. Dokážeš z toho něco vyvodit pro 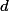 nebo
nebo 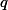 ?
?
(b)+ skrytý text
Pro x nedělitelné třemi se první exponent zjednoduší.
Úloha 6
(a)+ skrytý text
Kolik je skupin dvaceti lidí, které společný idol naopak obsahují?
(b)+ skrytý text
Odebírej z kraje, ke kolika nejvíc může být někdo na kraji vzdálený d?
Úloha 7
(a)+ skrytý text
Je to čtvrtina počtu stromů.
(b)+ skrytý text
Využij Bézoutovu rovnost pro  a
a 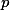 -- kdy jsou tato čísla nesoudělná?
-- kdy jsou tato čísla nesoudělná?
Matematika v příspěvcích
Do příspěvků lze vkládat matematické vzorce napsané v TeXu. Seznam značek naleznete na této stránce.
RSS kanály
Pokud chcete mít přehled o nejnovějších příspěvcích, použijte RSS:




