Marek Valkovič | org | 7. 3. 2026 13:33:47
Zdarec, máme pro Vás hintíky na kombinatorickou sérii.
Úloha 1 + skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
Úloha 4 + skrytý text
Úloha 5 + skrytý text
Úloha 6 + skrytý text
Úloha 7 + skrytý text
Úloha 8 + skrytý text
Úloha 1 + skrytý text
Větrný mlýn
Úloha 2 + skrytý text
Použij princip inkluze a exkluze
Úloha 3 + skrytý text
Prostřední políčko se nemůže zvětšit
Úloha 4 + skrytý text
Použij prefixové součty
Úloha 5 + skrytý text
Jde to!
Úloha 6 + skrytý text
Každému předmětu přiřaď dva úseky, které jím končí.
Úloha 7 + skrytý text
Ne + skrytý text
Kdyby bylo na začátku o elektron více, než bylo, jak by to vypadalo na konci?
Úloha 8 + skrytý text
Odhadni zdola nejmenší počet přátelských dvojic, ve kterých se nějaký vrchol nachází, pomocí stupňů jeho sousedů.
Tereza Matějková | org | 15. 2. 2026 16:00:51
Ahoj, určitě se nemůžeš dočkat až pomocí hintů vyřešíš zbytek úložek z 1. jarní série.
Úloha 1 + skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
Úloha 4 + skrytý text
Úloha 5 + skrytý text
Úloha 6 + skrytý text
Úloha 7 + skrytý text
Úloha 8 + skrytý text 
Úloha 1 + skrytý text
Předpokládej, že David mluví pravdu (objednal si salát), což Tě dovede ke sporu, tedy musí lhát. Obdobně takto postupně předpokládej jednotlivé osoby, až dojdeš k výsledku.
Úloha 2 + skrytý text
Všimni si, že před příchodem prohry nikdy nechceš vsadit více než polovinu svého jmění. Po prohře už můžeš vsázet všechno.
Úloha 3 + skrytý text
Uvaž tři největší, sečti je a umocni.
Úloha 4 + skrytý text
Přenášej úhly jako zběsilý. Mimo jiné Ti v rámci pětiúhelníku vzniknou kosočtverce.
Úloha 5 + skrytý text
Přenásob dokazovanou nerovnost čtyřkou. Každý člen v sumě pak zvlášť odhadni shora pomocí AG nerovnosti.
Úloha 6 + skrytý text
Použij indukci, ale nezapomeň rozebrat případy.
Úloha 7 + skrytý text
Pro horní odhad si vzpomeň na prvočísla. Pro příklad konstrukce pro možné hodnoty na základní větu aritmetiky.
Úloha 8 + skrytý text
Marek Valkovič | org | 7. 1. 2026 12:39:31
Ahoj, přinášíme ti hintíky na anglickou sérii.
Úloha 1 + skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
Úloha 4 + skrytý text
Úloha 5 + skrytý text
Úloha 6 + skrytý text
Úloha 7 + skrytý text
Úloha 8 + skrytý text
Úloha 1 + skrytý text
Urči pořadí zbytků modulo 3.
Úloha 2 + skrytý text
Podívej se na nejmenší číslo.
Úloha 3 + skrytý text
Uvědom si, že přičítáním 2 dostaneme všechny indexy od 1 do 2025.
Úloha 4 + skrytý text
Kvadratické zbytky modulo 4 jsou pouze 0 a 1.
Úloha 5 + skrytý text
Zkus použít Dirichletův princip.
Úloha 6 + skrytý text
Podívej se na permutace sloupců a řádků v součtové tabulce.
Úloha 7 + skrytý text
Pro spor předpokládej  a podívej se na
a podívej se na 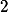 -valuace v
-valuace v 
Úloha 8 + skrytý text
Zamysli se, jak se chovají exponenty. + skrytý text
Najdi za sebou jdoucí Fibonnaciho čísla s dobrými zbytky modulo 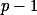
Tereza Matějková | org | 15. 12. 2025 22:01:26
Ahoj, určitě se těšíš až vyřešíš i zbytek úložek z 3. podzimní série pomocí hintů
Úloha 1+ skrytý text
Úloha 2+ skrytý text
Úloha 3+ skrytý text
Úloha 4+ skrytý text
Úloha 5+ skrytý text
Úloha 6 (hint 1)+ skrytý text
Úloha 6 (hint 2)+ skrytý text
Úloha 7 (hint 1)+ skrytý text
Úloha 7 (hint 2)+ skrytý text
Úloha 7 (hint 3)+ skrytý text
Úloha 8 (hint 1)+ skrytý text
Úloha 8 (hint 2)+ skrytý text
Úloha 8 (hint 3)+ skrytý text
Úloha 1+ skrytý text
musíš najít dláždění 
Úloha 2+ skrytý text
Podívej se modulo 2 a modulo 3
Úloha 3+ skrytý text
nejdřív si postav okraj. Puzzle musí mít rozměr 
Úloha 4+ skrytý text
Dosaď dvojice  a
a  . Pak substituuj
. Pak substituuj  .
.
Úloha 5+ skrytý text
Vyjádři si a, b, c, d pomocí čtyř čísel tak, že každé z a, b, c, d je součin nějakých dvou z nich.
Úloha 6 (hint 1)+ skrytý text
Stačí ukázat, že |AF|=|AE| a zbylé cyklické rovnosti
Úloha 6 (hint 2)+ skrytý text
Mocnost vrcholů ke kružnicím nad protějšími stranami
Úloha 7 (hint 1)+ skrytý text
Zkus dokázat, že je funkce bijekce.
Úloha 7 (hint 2)+ skrytý text
Trik - několikrát za  dosaď
dosaď  .
.
Úloha 7 (hint 3)+ skrytý text
Vyjádři si  ,
,  a
a  a dojdi k rovnosti.
a dojdi k rovnosti.
Úloha 8 (hint 1)+ skrytý text
Nakresli si to v geogebře.
Úloha 8 (hint 2)+ skrytý text
Všimni si, že body  a
a 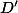 jsou vždy souměrné podle osy úsečky
jsou vždy souměrné podle osy úsečky 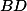 .
.
Úloha 8 (hint 3)+ skrytý text
Uvědom si, že délka  se v zobrazení zachovává.
se v zobrazení zachovává.
Marek Valkovič | org | 4. 11. 2025 10:22:56
Ahoj, určitě se nemůžeš dočkat, až vyřešíš zbytek úložek pomocí našich hintů.
Úloha 1+ skrytý text
Úloha 2+ skrytý text
Úloha 3+ skrytý text
Úloha 4+ skrytý text
Úloha 5+ skrytý text
Úloha 6+ skrytý text
Úloha 7+ skrytý text
Úloha 8+ skrytý text
Úloha 1+ skrytý text
Narýsuj dvě úhlopřícky a použij jejich průsečík.
Úloha 2+ skrytý text
Využij vlastnosti rovnoramenných trojúhelníků.
Úloha 3+ skrytý text
Ukaž, že  je rovnoramenný.
je rovnoramenný.
Úloha 4+ skrytý text
Spočítej poloměry z délek stran.
Úloha 5+ skrytý text
Dokresli bod dotyku 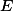 kružnice
kružnice  -připsané se stranou
-připsané se stranou 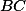 .+ skrytý text
.+ skrytý text
Střední příčka v 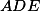 .
.
Úloha 6+ skrytý text
Označ si průsečík 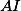 s
s 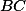 jako
jako  a dokaž, že
a dokaž, že  je podobný
je podobný  . Obdobně pro zbylé strany
. Obdobně pro zbylé strany 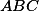 .
.
Úloha 7+ skrytý text
Na osách úhlů trojúhelníku leží střed kružnice vepsané a Švrčkovy body, které lokalizují polohu vepsiště.
Úloha 8+ skrytý text
Při čtyřech bodech na kružnici umíme nakreslit osy tětiv.+ skrytý text
Nakresli vepsšitě 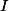 a poté
a poté  - a
- a 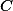 -připsiště trojúhelníku
-připsiště trojúhelníku  .
.
Lukáš Trojan | org | 3. 10. 2025 12:55:24
Ahojky, přináším hinty k 1. podzimní sérii:
Úloha 1 + skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
Úloha 4 + skrytý text
Úloha 5 + skrytý text
Úloha 6 + skrytý text
Úloha 7 + skrytý text
Úloha 8 + skrytý text
Úloha 1 + skrytý text
V -> X
Úloha 2 + skrytý text
Diagonály liché délky musí mít alespoň jednu pozici prázdnou
Úloha 3 + skrytý text
řešení je 3
Úloha 4 + skrytý text
Vyber si jednoho vojáka a všech ostatních se ptej na tohoto vojáka.
Úloha 5 + skrytý text
Osová souměrnost podle CM
Úloha 6 + skrytý text
postupně zvětšuj mnozinu 
Úloha 7 + skrytý text
Postupně zvětšuj počet prvočíselných dělitelů aktuálního čísla a neboj se mocnin.
Úloha 8 + skrytý text
Vyrob si graf hry, zamysli se, kolik stavů vede do stejného stavu a do jakých stavů se dá ze stavu dostat.
Johana Kubatová | org | 29. 5. 2025 10:38:28
Ahoj! Určitě už se nemůžeš dočkat poslední várky hintů letošní série :)
Úloha 1
(a)+ skrytý text
(b)+ skrytý text
Úloha 2
(a)+ skrytý text
(b)+ skrytý text
Úloha 3
(a)+ skrytý text
(b)+ skrytý text
Úloha 4
(a)+ skrytý text
(b)+ skrytý text
Úloha 5
(a)+ skrytý text
(b)+ skrytý text
Úloha 6
(a)+ skrytý text
(b)+ skrytý text
Úloha 7
(a)+ skrytý text
(b)+ skrytý text
Úloha 1
(a)+ skrytý text
Rozepiš to a najdi dělitelnost osmi.
(b)+ skrytý text
Parita.
Úloha 2
(a)+ skrytý text
Mnohostěny nemusí být všechny stejného typu.+ skrytý text
Čtyřstěn a osmistěn.
(b)+ skrytý text
Pomocí obsahů stěn spočítej různými způsoby objem čtyřstěnu.+ skrytý text
CS.
Úloha 3
(a)+ skrytý text
Podívej se na součet čísel na tabuli.
(b)+ skrytý text
Podívej se na součet čtverců čísel na tabuli.
Úloha 4
(a)+ skrytý text
Sleduj počet levých bot v posouvajícím se úseku 10 bot.
(b)+ skrytý text
Nejprve vyřeš problém pro cykly.
Úloha 5
(a)+ skrytý text
Vyjádři si rovnost  pro několik různých
pro několik různých  . Dokážeš z toho něco vyvodit pro
. Dokážeš z toho něco vyvodit pro 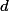 nebo
nebo 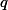 ?
?
(b)+ skrytý text
Pro x nedělitelné třemi se první exponent zjednoduší.
Úloha 6
(a)+ skrytý text
Kolik je skupin dvaceti lidí, které společný idol naopak obsahují?
(b)+ skrytý text
Odebírej z kraje, ke kolika nejvíc může být někdo na kraji vzdálený d?
Úloha 7
(a)+ skrytý text
Je to čtvrtina počtu stromů.
(b)+ skrytý text
Využij Bézoutovu rovnost pro  a
a 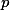 -- kdy jsou tato čísla nesoudělná?
-- kdy jsou tato čísla nesoudělná?
Vera | 29. 5. 2025 07:31:07
You actually reported that really well.
casino en ligne
Fantastic info, Regards.
meilleur casino en ligne
Amazing a good deal of superb knowledge.
casino en ligne France
Thanks. Wonderful information!
casino en ligne fiable
Thanks. I enjoy it!
casino en ligne
Wow a good deal of wonderful material!
casino en ligne
This is nicely said. !
casino en ligne
Kudos! Great stuff!
meilleur casino en ligne
Beneficial information Regards.
casino en ligne France
You've made your point quite nicely..
casino en ligne
casino en ligne
Fantastic info, Regards.
meilleur casino en ligne
Amazing a good deal of superb knowledge.
casino en ligne France
Thanks. Wonderful information!
casino en ligne fiable
Thanks. I enjoy it!
casino en ligne
Wow a good deal of wonderful material!
casino en ligne
This is nicely said. !
casino en ligne
Kudos! Great stuff!
meilleur casino en ligne
Beneficial information Regards.
casino en ligne France
You've made your point quite nicely..
casino en ligne
Lukáš Trojan | org | 9. 4. 2025 11:31:28
Ahojky, tady jsou hinty k 3. jarní sérii a 3. seriálové sérii:
3. jarní série
Úloha 1 + skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
Úloha 4 + skrytý text
Úloha 5 + skrytý text
Úloha 6 + skrytý text
Úloha 7 + skrytý text
Úloha 8 + skrytý text
3. seriálová série
Úloha 1 + skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
3. jarní série
Úloha 1 + skrytý text
dej třeba do řádku 7 buků a do jiného řádku ten jeden zbylý.
Úloha 2 + skrytý text
zkus lichá čísla a doplň je.
Úloha 3 + skrytý text
Jde to, rozděl případy. Pomůže ti, že José může vyslat na jednu pěšinku skupinku všech čtyř a poté tuto pěšinku prověřit sám. Tím zjistí, kdo je nezbedný.
Úloha 4 + skrytý text
Počet hran na obvodu čtverce roste lineárně s délkou strany čtverce, kdežto počet hran uvnitř roste kvadraticky.
Úloha 5 + skrytý text
Když  ,
,  ,
,  přenásobíš přirozeným číslem, rovnost pořád platí
přenásobíš přirozeným číslem, rovnost pořád platí
Úloha 6 + skrytý text
Podívej se na vztah modulo p a (p-1).
Úloha 7 + skrytý text
Konstruuj induktivně
Úloha 8 + skrytý text
Převeď poměr délek stran na poměr obsahů
+ skrytý textUvažuj trojúhelník  nejmenšího obsahu. Vydláždi osmiúhelník vhodnými rovnoběžníky.
nejmenšího obsahu. Vydláždi osmiúhelník vhodnými rovnoběžníky.
3. seriálová série
Úloha 1 + skrytý text
Vytkni 
Úloha 2 + skrytý text
koeficient u  v
v  .
.
Úloha 3 + skrytý text
Vyrob mocninné řady a dívej se na  .
.
+ skrytý textVyjádři  , vztah mocninných řad ukáže konstrukci.
, vztah mocninných řad ukáže konstrukci.
Johana Kubatová | org | 8. 3. 2025 08:23:05
Ahoj! Nová várka hintů je tady! :)
Úloha 1+ skrytý text
Úloha 2+ skrytý text
Úloha 3+ skrytý text
Úloha 4+ skrytý text
Úloha 5+ skrytý text
Úloha 6+ skrytý text
Úloha 7+ skrytý text
Úloha 8+ skrytý text
Úloha 1+ skrytý text
Existuje. Kolik tupých úhlů můžeš dostat z jednoho úhlu v původním čtyřúhelníku?
Úloha 2+ skrytý text
Použij středový a obvodový úhel.
Úloha 3+ skrytý text
Ukaž soustavou čtverců, že vybraný bod musí být nulový.
Úloha 4+ skrytý text
Ať Ben určí rovinu skrze střed glóbu a nějaké dva body na glóbu. Kolik bodů může takto z glóbu odebrat?
Úloha 5+ skrytý text
Omezíš-li se na 3 státy, kolik mezi nimi může jezdit trajektů?
Úloha 6+ skrytý text
Zkus kromě osové souměrnosti i něco otočit.
Úloha 7+ skrytý text
N nad dvěma žiraf stačí. + skrytý text
Nech Miška se postupně zbavovat dvojic ohrádek, které mají stejný počet žiraf.
Úloha 8+ skrytý text
Posuň C o vektor střed 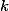 a střed
a střed  .+ skrytý text
.+ skrytý text
Posuň C o vektor 2x střed 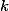 a střed
a střed  .
.
Lukáš Trojan | org | 7. 2. 2025 21:10:31
Ahojky, tady jsou hinty k 1. jarní sérii a 2. seriálové sérii :D
1. jarní série
Úloha 1 + skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
Úloha 4 + skrytý text
Úloha 5 + skrytý text
Úloha 6 + skrytý text
Úloha 7 + skrytý text
Úloha 8 + skrytý text
2. seriálová série
Úloha 1+ skrytý text
Úloha 2 + skrytý text
Úloha 3 + skrytý text
1. jarní série
Úloha 1 + skrytý text
Co se děje se zápornými čísly?
Úloha 2 + skrytý text
Použij součtový vzorec: 
Úloha 3 + skrytý text
Děl se zbytkem.
Úloha 4 + skrytý text
Samé odhady zezdola, ale co najít nějaký shora?
Úloha 5 + skrytý text
Jak rychle roste ciferný součet? O kolik musíš zvýšit  , aby se tak stalo?
, aby se tak stalo?
Úloha 6 + skrytý text
Je daný trojúhelník 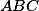 s ortocentrem
s ortocentrem 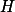 . Nech
. Nech 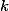 ,
,  jsou přímky, které se dotýkají kružnice opsané trojúhelníku
jsou přímky, které se dotýkají kružnice opsané trojúhelníku 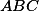 postupně v bodech
postupně v bodech  ,
, 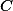 . Nechť
. Nechť  je kružnice so středem ležícím na
je kružnice so středem ležícím na 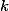 , která prochází body
, která prochází body  a
a 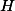 . Podobně nechť
. Podobně nechť  je kružnice so středem ležícím na
je kružnice so středem ležícím na  , která prochází body
, která prochází body 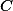 a
a 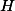 . Kružnice
. Kružnice  a
a  se protnou podruhé v bodě
se protnou podruhé v bodě  . Dokaž, že těžiště trojúhelníka
. Dokaž, že těžiště trojúhelníka 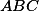 leží na
leží na  .
.
Úloha 7 + skrytý text
Lze z počtu pro 2024 cifer určit počet pro 2025 cifer?
Úloha 8 + skrytý text
Porovnej členy v sumě s binomickými koeficienty
2. seriálová série
Úloha 1+ skrytý text
Nejdřív odvoď  .
.
+ skrytý textVyvoď, že sudá i lichá  dávají liché
dávají liché 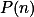 .
.
Úloha 2 + skrytý text
K výhře stačí mít poslední tah.
+ skrytý textJsou-li dány absolutní a vedoucí koeficient, zbývá jen konečně mnoho racionálních čísel, která by se mohla stát kořenem.
Úloha 3 + skrytý text
Použij Henselovo lemma. Pokud by to nešlo, najdi spor v tom, jak rychle rostou polynomy vyššího a menšího stupně
Johana Kubatová | org | 11. 1. 2025 10:07:40
Ahoj, stále se marně pokoušíš vyřešit nějakou úložku 4. podzimní série? Nová várka hintů ti určitě pomůže:)
Úloha 1+ skrytý text
Úloha 2+ skrytý text
Úloha 3+ skrytý text
Úloha 4+ skrytý text
Úloha 5+ skrytý text
Úloha 6+ skrytý text . If
. If  , Majda can decrease number of inverses in each turn (inverse is a pair of numbers in the wrong order). For
, Majda can decrease number of inverses in each turn (inverse is a pair of numbers in the wrong order). For  , consider the last turn before Majda wins.
, consider the last turn before Majda wins.
Úloha 7+ skrytý text
Úloha 8+ skrytý text
Úloha 1+ skrytý text
Hint: Fix  pigs and look at the positions where Matouš, Matěj adn Michal can be put.
pigs and look at the positions where Matouš, Matěj adn Michal can be put.
Úloha 2+ skrytý text
The original sum of the clock number pairs is constant, but the performed number of modulo operations is not.
Úloha 3+ skrytý text
Permute the points  ,
, ,
,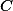 .
.
Úloha 4+ skrytý text
Look at the different permutations of  modulo
modulo  .
.
Úloha 5+ skrytý text
Think first about the situation when Vítek takes only the first card from the top of the deck and puts it somewhere else.
Úloha 6+ skrytý text
Úloha 7+ skrytý text
Fix one permutation  and look at the mean value of
and look at the mean value of  just over the permutations
just over the permutations  with
with  independent of
independent of  .
.
Úloha 8+ skrytý text
Match ways of the rich one to ways of the poor one in some order such that the rich one pays more in each pair (or the same)+ skrytý text
What happens when both stand next to an edge which they can both still take? How much do they pay in their next step?
Lukáš Trojan | org | 12. 12. 2024 18:18:38
hinty 3. podzimní série a 1. seriálové série jsou tady:
1. jarní série
Úloha 1 + skrytý text
Úloha 2 + skrytý text .
.
Úloha 3 + skrytý text
Úloha 4 + skrytý text
Úloha 5 + skrytý text
Úloha 6 + skrytý text
Úloha 7 + skrytý text
Úloha 8 + skrytý text
1. seriálová série
Úloha 1 + skrytý text
Úloha 2 + skrytý text má lichý stupeň, zatímco
má lichý stupeň, zatímco  i
i  sudý. Vedoucí členy
sudý. Vedoucí členy  a
a  se tak musí vyrušit, to už určí stupeň.
se tak musí vyrušit, to už určí stupeň.
Úloha 3+ skrytý text
1. jarní série
Úloha 1 + skrytý text
Jaký zbytek má  mod
mod 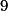 a mod
a mod  ?
?
Úloha 2 + skrytý text
Úloha 3 + skrytý text
Podívej se na zbytky po dělení pěti.
Úloha 4 + skrytý text
Dosaď  a uvažuj, jakou délku může mít cyklus, v němž
a uvažuj, jakou délku může mít cyklus, v němž 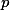 leží.
leží.
Úloha 5 + skrytý text
BÚNO je  liché, pak vol
liché, pak vol 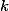 tak, aby hned
tak, aby hned  byla mocnina dvojky.
byla mocnina dvojky.
Úloha 6 + skrytý text
Co se děje s rozdíly délek stran?
Úloha 7 + skrytý text
Je to jen  .
.
+ skrytý textDokaž nerovnost  sporem, potom už to bude easy.
sporem, potom už to bude easy.
Úloha 8 + skrytý text
zvol nějaké prvočíslo  takové, že všechna počáteční čísla na tabuli splňují
takové, že všechna počáteční čísla na tabuli splňují  .
.
+ skrytý textDokaž, že tato vlastnost se zachová při tvorbě nových čísel.
+ skrytý textzvol klidně celé 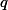 takové, že
takové, že  .
.
1. seriálová série
Úloha 1 + skrytý text
Rozepiš si Vietovy vztahy.
Úloha 2 + skrytý text
Úloha 3+ skrytý text
Znáš většinu kořenů  . Ty zbylé dopočítej z Vietových vztahů.
. Ty zbylé dopočítej z Vietových vztahů.
Johana Kubatová | org | 16. 11. 2024 07:54:31
Ahoj, nemůžeš se dočkat hintů 2. podzimní série? Hle, tady jsou:
Úloha 1+ skrytý text
Úloha 2+ skrytý text
Úloha 3+ skrytý text
Úloha 4+ skrytý text
Úloha 5+ skrytý text
Úloha 6+ skrytý text
Úloha 7+ skrytý text
Úloha 8+ skrytý text
Úloha 1+ skrytý text
Nech 5 stěn souvislých a jednu rozřež.+ skrytý text
.....^.....
.....#.....
.<###>.
.....#.....
.....v.....
.....^.....
.....#.....
.<###>.
.....#.....
.....v.....
Úloha 2+ skrytý text
Zatáčka pokryje půl stěny dvojmo.
Úloha 3+ skrytý text
Začni s rovinou, které prochází třemi vrcholy, a posouvej ji tak, aby nakonec procházela dalšími šesti vrcholy.+ skrytý text
Spojitostí musel řez v nějakém okamžiku být pravidelným šestiúhelníkem.
Úloha 4+ skrytý text
Stačí to řešit v rovině.+ skrytý text
Všechny tečny z libovolného bodu jsou stejně dlouhé.
Úloha 5+ skrytý text
Podívej se na nejdelší hranu a dvojice hran, které "vycházejí" z jejích koncových bodů.+ skrytý text
Kdyby ani jedna možnost nedávala funkční trojici, najdi spor sečtením trojúhelníkových nerovností v trojúhelnících obsahujících nejdelší hranu.
Úloha 6+ skrytý text
Uvaž orientovanou cestu z vrcholu stupně alespoň čtyři do vrcholu stupně nanejvýš dva. Co když obrátíš všechny hrany na této cestě?
Úloha 7+ skrytý text
Označte si průsečíky přímek se stěnami a vezměte ten nejblíže  .
.
Úloha 8+ skrytý text
Ukažte, že tyto průměty leží na sféře nad průměrem  . Stereografická projekce posílá kružnice na kružnice.
. Stereografická projekce posílá kružnice na kružnice.
Lukáš Trojan | org | 7. 10. 2024 17:53:28
Ahojky, pořád nevíš jak vyřešit nějakou úlohu z 1. podzimní série? Hinty jsou tu pro tebe. :D
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text i
i  mají být mocniny
mají být mocniny 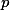 , takže
, takže  .
.
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Body tvoří trojúhelník právě když neleží na přímce
Úloha 2. + skrytý text
Jedničku nech stranou, pak vyráběj čtveřice, jež se vynulují.
Úloha 3. + skrytý text
Zápis ve dvojkové soustavě je jednoznačný.
Úloha 4. + skrytý text
Kdykoliv slovo obsahuje lišekrát  i
i  , změn v prvním výskytu kteréhokoliv z nich
, změn v prvním výskytu kteréhokoliv z nich 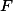 na
na 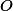 či obráceně.
či obráceně.
Úloha 5. + skrytý text
Zkus napočítat, kolik alespoň políček splňuje podmínku pro svůj řádek, nebo pro svůj sloupec (ne nutně obojí).
Úloha 6. + skrytý text
Bude to dokonce kosočtverec. Ukaž, že CD a EF se navzájem půlí.
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Zjisti poměr obsahů trojúhelníků MAC a MBD.
Denisa Hanušková | org | 8. 5. 2024 19:52:57
Ahoj, nedá Ti některá úložka z myš-maše spát? Hinty Ti pomůžou.
Úloha 1.
a)+ skrytý text
b)+ skrytý text
Úloha 2.
a)+ skrytý text
b)+ skrytý text
Úloha 3.
a)+ skrytý text
b)+ skrytý text
Úloha 4.
a)+ skrytý text
b)+ skrytý text
Úloha 5.
a)+ skrytý text
b)+ skrytý text
Úloha 6.
a)+ skrytý text
b)+ skrytý text
Úloha 7.
a)+ skrytý text
b)+ skrytý text
Úloha 1.
a)+ skrytý text
Postupuj indukcí, v každém kroku si postupně tipni všechny výsledky pro jednoho zápasníka.
b)+ skrytý text
Veselá množina leží na dvou rovnoběžkách s AB. Středová souměrnost zachovává paritu souřadnic.
Úloha 2.
a)+ skrytý text
Slož spoustu T-tetromin vedle sebe.
b)+ skrytý text
Přelož úlohu na počítání dělitelů jisté konstanty, které ale nejsou příliš malé.
+ skrytý text
+ skrytý text
Dělitelé nějakého daného 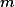 se párují do dvojiček
se párují do dvojiček 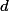 ,
, 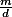 .
.
Úloha 3.
a)+ skrytý text
Uvažuj, kde se protínají osy úhlů
b)+ skrytý text
Vystejnolehli kružnici  -připsanou z
-připsanou z  s koeficientem
s koeficientem 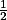 .
.
+ skrytý text
+ skrytý text
Soustředné kružnice, dotýkající se tětivy!
Úloha 4.
a)+ skrytý text
Geometrická posloupnost.
b)+ skrytý text
Podívej se na 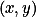 jako na bod v rovině s trojúhelníčkovou sítí.
jako na bod v rovině s trojúhelníčkovou sítí.
+ skrytý text 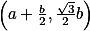 popisuje bod trojúhelníčkové sítě, použij nějaký blízký.
popisuje bod trojúhelníčkové sítě, použij nějaký blízký.
+ skrytý text
Úloha 5.
a)+ skrytý text
Podívej se, v které posloupnosti leží součin diferencí.
b)+ skrytý text
Podívej se na "hustotu" na všech číslech a na sudých číslech.
Úloha 6.
a)+ skrytý text
Mohlo. Zkus to prostě zkonstruovat.
b)+ skrytý text
Hledej podobné trojúhelníky.
Úloha 7.
a)+ skrytý text
Jaká prvočísla jsou potenciálně vůbec k dispozici?
b)+ skrytý text
Uvažuj nějakou sousedící dvojici vrcholů a ukaž, že na každého souseda prvního vrcholu přísluší nějaký soused druhého vrcholu. Jak tomu bude, když původní dvojice nesousedí?
José | org | 12. 4. 2024 21:49:55
Hola hej, hola hou!
Hintíky už k tobě jdou! :D
3. jarní série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
3. seriálová série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Hintíky už k tobě jdou! :D
3. jarní série
Úloha 1. + skrytý text
Prostě to udělej! ;)
Úloha 2. + skrytý text
Párů je 151, což je jen kousek od 150.
Úloha 3. + skrytý text
Áďa to dokáže. + skrytý text
Když uděláš z čísel dost velkou ohrádku, vejdou se všechna i dovnitř.
Úloha 4. + skrytý text
Odhadni, kolik může být duplicit mezi kartami. + skrytý text
Pro konstrukci začni s úplným grafem, symboly nechť jsou hrany. To ale nebude úplně stačit.
Úloha 5. + skrytý text
Uvaž matfyzáka, který tančil s nejvíce matfyzačkami. + skrytý text
A pak matfyzačku, která s ním netančila.
Úloha 6. + skrytý text
Zkus si lidi představit jako vrcholy grafu s hranami dvou barev (jedna barva odpovídá Kecalovu plánu, druhá Kecalčině). Jak tento graf vypadá (resp. jak vypadají jeho souvislé komponenty)?
Úloha 7. + skrytý text
Všimni si, že 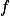 a
a 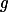 musí být bijekce.
musí být bijekce.
Úloha 8. + skrytý text
Co kdyby Klárka nejdříve chtěla získat alespoň tolik pravých rukavic jako levých... + skrytý text
a ve správnou chvíli strategii změnila?
3. seriálová série
Úloha 1. + skrytý text
Pomocí poměrů spočítej body 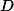 a
a 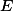 . Pak pomocí vzorečků a podobností počítej jednotlivé přímky.
. Pak pomocí vzorečků a podobností počítej jednotlivé přímky.
Úloha 2. + skrytý text
Ze seriálu víme, že platí 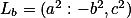 ,
, 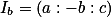 . Průsečík přímek pak už dokážeš snadno spočítat.
. Průsečík přímek pak už dokážeš snadno spočítat.
Úloha 3. + skrytý text
Je-li 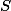 průsečík
průsečík 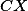 a
a 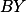 , zajistíš rovnoběžnost tak, že
, zajistíš rovnoběžnost tak, že 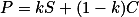 a
a 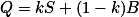 . Zvol si souřadnice bodů
. Zvol si souřadnice bodů  ,
,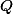 ,
,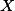 ,
,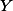 co nejjednodušeji. + skrytý text
co nejjednodušeji. + skrytý text
Chordálu získáš jako rozdíl rovnic kružnic. Pro důkaz, že přímky prochází jedním bodem, spočítej determinant.
Denisa Hanušková | org | 6. 3. 2024 08:57:39
Ahoj, nová várka hintů je zde, s nimi hravě dořešíš úlohy 2. jarní série.
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
Úloha 1.+ skrytý text
23. účastník je kamarád všech, takže i 1. účastníka.
Úloha 2.+ skrytý text
Umísti kamarády k prostřednímu sloupu.
Úloha 3.+ skrytý text
Uvaž největší místnost v libovolných dvou po sobě jdoucích kolech.
Úloha 4.+ skrytý text
Stačí ukázat, že kamarád průsečíku leží na výšce z  .
.
Úloha 5.+ skrytý text
Všichni moji přátelé se přátelí navzájem.
Úloha 6.+ skrytý text
Najdi švrčkův bod
Úloha 7.+ skrytý text
Překlop 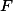 podle stran.
podle stran.
Úloha 8.+ skrytý text
Ukaž, že 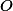 a
a 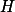 jsou kamarádi v čtyřúhelníku
jsou kamarádi v čtyřúhelníku 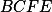 , tudíž
, tudíž 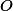 leží na ose
leží na ose 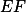 .
.
José | org | 7. 2. 2024 15:21:21
Za týden je svátek zamilovaných. A kdo by nemiloval hinty 1j a 2s série ;).
1. jarní série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
2. seriálová série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
1. jarní série
Úloha 1. + skrytý text
Zkus napsat spoustu trojiček se součtem 6.
Úloha 2. + skrytý text
Všimni si, že nsn si od každého prvočísla vybere tu největší vyskytující se mocninu.
Úloha 3. + skrytý text
Znaménko rozdílu se může změnit nanejvýš jednou.
Úloha 4. + skrytý text
Najdi prosté zobrazení z počtu způsobů pro n do počtu způsobů pro n+1.
Úloha 5. + skrytý text
Dívej se na racionální čísla modulo 5.
Úloha 6. + skrytý text
Posviť si na posloupnost bn = √(an+1 + an).
Úloha 7. + skrytý text
Fn je Fibonacciho číslo, Gn je od jistého okamžiku rozdíl dvou Fibonacciho posloupností.
Úloha 8. + skrytý text
Celočíselné body na hyperbole x^2 - 2cxy + y^2 + c^2 - 1 = 0.
2. seriálová série
Úloha 1. + skrytý text
Použij vzorce pro otáčení (vrcholy čtverců nad stranami) a pro rovnoběžník.
Úloha 2. + skrytý text
Vzorec ortocentra trojúhelníka na jednotkové kružnici máš, |a-b| = √((a-b)(a-b)). + skrytý text
Pozn. (a-b) zde značí číslo komplexně sdružené.
Pak si jen vzpomeň na vzorce:
.ζk = ζ7-k,
ζ7+k = ζk.
.ζk = ζ7-k,
ζ7+k = ζk.
Pozn. (a-b) zde značí číslo komplexně sdružené.
Úloha 3. + skrytý text
Vepsaná kružnice je jednotková, vzorec na průsečík tečny s tětivou máš. To nejhorší se pokrátí.
José | org | 13. 1. 2024 07:17:51
Due to technical difficulties, we are currently unable to post mathematical text in this chat, forcing us to post this next series of hints as plain text. We hope to get the issue resolved soon, so that we can post a more readable version in the near future. We apologize for the inconvenience.
Problem 1. + skrytý text
Problem 2. + skrytý text
Problem 3. + skrytý text
Problem 4. + skrytý text
Problem 5. + skrytý text
Problem 6. + skrytý text
Problem 7. + skrytý text
Problem 8. + skrytý text
Problem 1. + skrytý text
Pigs eat more food than chickens.
Problem 2. + skrytý text
Square it, then arrange it into a square.
Problem 3. + skrytý text
Show that any triangle placed completely inside a unit square has an area of at most 1/2.
Problem 4. + skrytý text
Divide out what you can, you will be left with a product of |m-n|/2 bigger numbers vs a product of |m-n|/2 smaller numbers.
Problem 5. + skrytý text
Use the AM-GM inequality.
Problem 6. + skrytý text
For each divisor d, calculate how many times it will be counted in the sum. + skrytý text
Get a bound on the sum using floor(n/d) - floor(n/(d+1)) >= 0.
Problem 7. + skrytý text
Square the given recurrence relations. + skrytý text
You only need to show (x_n)^2 + (y_n)^2 + (z_n)^2 > 6n+39.
Problem 8. + skrytý text
Use the sum formula. + skrytý text
And apply Cauchy–Schwarz.
Kalendář
-
13. března 2026
Matematický Náboj (link) -
14. března 2026
Jarní PraSečí výlet -
6. dubna 2026
Termín odevzdání 3. jarní série




