Štěpán | 19. 5. 2011 18:32:45
jo, stačilo, děkuju
Pepa T. | 18. 5. 2011 23:43:38
Věnuju dokonce (byť schematický) popis řešení: Dokresli připsiště 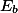 ,
, 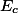 trojúhelníka
trojúhelníka 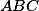 vzhledem k
vzhledem k 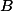 a
a 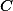 a ukaž, že kružnice opsaná
a ukaž, že kružnice opsaná 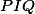 je vlastně kružnicí opsanou
je vlastně kružnicí opsanou 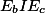 (přímka
(přímka 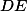 je chordála). A pak si už jen vzpomeň na Feuerbachovu kružnici :). Stačilo? Nebo ještě?
je chordála). A pak si už jen vzpomeň na Feuerbachovu kružnici :). Stačilo? Nebo ještě?
Tonda | 18. 5. 2011 18:58:05
Štěpán: No už vím jak se dělá 3b, dám ti hint jestli chceš :)
Štěpán | 18. 5. 2011 18:33:55
Pepo, nechceš věnovat nějaký hint k 3b?
pavel | 18. 5. 2011 13:15:38
Ja teda nevim, ktery z tech kroku presne wolfram neumi. Nejspis asi proste neumi zkombinovat vsechny tri, ale kazdopadne
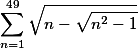
uz zvladne :) (http://www.wolframalpha.com/input/?i=sum_{n%3...)
uz zvladne :) (http://www.wolframalpha.com/input/?i=sum_{n%3...)
Pepa T. | 17. 5. 2011 19:04:49
Tak ať tu ta úloha nesmrdí tak dlouho, tak já popíšu tři triky, které se při řešení použijou:
1) Usměrnit zlomek: vynásobit jeho čitatel i jmenovatel výrazem
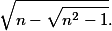
2) Odmocnit druhou mocninu: např.
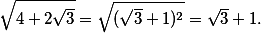
Tady je to podobné, akorát se přišmelí nějaká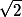 , aby to vyšlo líp. Pak totiž docela funguje, že
, aby to vyšlo líp. Pak totiž docela funguje, že 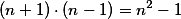 a
a 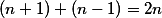 (tohle je ten krok, který wolfram neumí).
(tohle je ten krok, který wolfram neumí).
3) Zteleskopovat: Tím se myslí takový ten trik, že
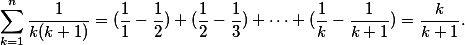
S tímhle návodem už by to nemělo být náročné ;-).
1) Usměrnit zlomek: vynásobit jeho čitatel i jmenovatel výrazem
2) Odmocnit druhou mocninu: např.
Tady je to podobné, akorát se přišmelí nějaká
3) Zteleskopovat: Tím se myslí takový ten trik, že
S tímhle návodem už by to nemělo být náročné ;-).
miso | 16. 5. 2011 17:22:57
kdo bych chtel resit maxima, minima, neco z funkcii najme operacie s funkciami aneb vse co vi nech se ozvi. Dam mu moj ID skype.Najme pre druhakov, tretiakov na strednych skolach.
Mirek Olšák | 13. 5. 2011 22:15:40
Je to tak, taky to uz umim, ale mam pocit, ze Wolfram to v zasade vyresil za mne. Holt v (olympiadni) algebre se tezko hleda Mathematico-vzdorna uloha podobne jako v geometrii geogebro-vzdorna...
Ale poscita se to pekne.
Ale poscita se to pekne.
pavel | 13. 5. 2011 20:27:31
Ale po prvnim kroku uz to Wolfram zvladne :-) (pokud nahodou neznate, urcite vyzkousejte http://www.wolframalpha.com/)
Vejtek | 13. 5. 2011 19:17:20
Ha, pěkný trik, který ani wolfram neumí!
PS: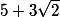
PS:
Pepa T. | 13. 5. 2011 13:18:24
Haha, našel jsem dobrou legrácku, tak se o ní nemůžu nepodělit :).
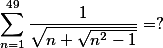
Za správný výsledek je čest a sláva, ale nepište postup, ať to neprokecnete ostatním :).
Za správný výsledek je čest a sláva, ale nepište postup, ať to neprokecnete ostatním :).
Štěpán | 11. 5. 2011 14:05:27
Olin: no to sice jo, ale to už je jen jednoduchá finta...
Mirek: nevím, jestli je platnost oné věty opravdu očividná, každopádně i kdyby byla, tak to neznamená, že je úloha lehká, protože se ještě člověk musí vydat tímto směrem...
Mirek: nevím, jestli je platnost oné věty opravdu očividná, každopádně i kdyby byla, tak to neznamená, že je úloha lehká, protože se ještě člověk musí vydat tímto směrem...
Olin | 11. 5. 2011 12:21:32
Mirek, Štěpán: Samozřejmě je zapotřebí to ještě trochu poupravit, protože Ramseyovka nám neříká, jakou "barvu" ta klika bude mít, zatímco v zadání je "barva" už stanovena.
Miroslav Olšák | 10. 5. 2011 22:05:00
Štěpán: Když myslíš... Ale jestli je platnost oné věty i její použití očividné, tak jak to, že to byla tak nezdolatelná úloha? Jinak, Anička Zavadilová prý to 4b vyřešila, tak jsem zvědavý.
Kenny | 10. 5. 2011 21:33:17
A vítězí Tondaaa, který tak vyřešil jedničku z amerického celostátka 2011!
Ale orgové se nenechávají zahanbit a vypisují druhou výzvu platnou do dnešní půlnoci!
Součet reálných čísel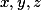 je 0. Dokažte, že platí
je 0. Dokažte, že platí
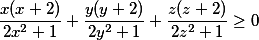
a najděte všechny případy, kdy nastává rovnost.
Dá to někdo za dvě a půl hodiny?
Ale orgové se nenechávají zahanbit a vypisují druhou výzvu platnou do dnešní půlnoci!
Součet reálných čísel
a najděte všechny případy, kdy nastává rovnost.
Dá to někdo za dvě a půl hodiny?
Tonda | 10. 5. 2011 20:50:48
Ahojte,
Nejprve podmínku opravíme na:
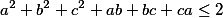
Dále celou nerovnost vynásobíme dvěma a po odečtení 3 od každé strany (od každého zlomku 1 )dostaneme ekvivalentní nerovnost
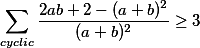
Nyní použijeme podmínku na pravou stranu
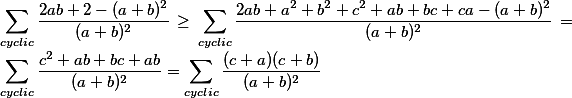
Po použití přimého AG na výše uvedený výraz dostaneme, že výraz je větší než 3, což chceme dokázat a celý postup můžeme obrátit, aproto náš důkaz platí. Rovnost nastane, právě tehdy, když nastane rovnost v posledním AG a při rovnosti v podmínce, aproto není těžké dopočítat, že to je: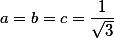
Nejprve podmínku opravíme na:
Dále celou nerovnost vynásobíme dvěma a po odečtení 3 od každé strany (od každého zlomku 1 )dostaneme ekvivalentní nerovnost
Nyní použijeme podmínku na pravou stranu
Po použití přimého AG na výše uvedený výraz dostaneme, že výraz je větší než 3, což chceme dokázat a celý postup můžeme obrátit, aproto náš důkaz platí. Rovnost nastane, právě tehdy, když nastane rovnost v posledním AG a při rovnosti v podmínce, aproto není těžké dopočítat, že to je:
Kenny | 10. 5. 2011 19:44:54
A já hned přidám jednu lehkou úlohu z celkem aktuální soutěže! Takže, řešitelé, pokud ji nevyřešíte do dnešní půlnoci (sem na chat), jste pěkné lamy! Tak dotoho!
Kladná reálná čísla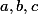 splňují
splňují 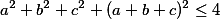
Dokažte, že
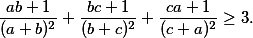
A přidám ještě drobnou motivaci. S Pavlem se chystáme vydat náš loňský seriál jako samostatnou brožurku, tak můžeme vítězi slíbit, že dostane podepsané vydání :P
Kladná reálná čísla
Dokažte, že
A přidám ještě drobnou motivaci. S Pavlem se chystáme vydat náš loňský seriál jako samostatnou brožurku, tak můžeme vítězi slíbit, že dostane podepsané vydání :P
Štěpán | 10. 5. 2011 19:01:46
to je v podstatě spíš řešení než hint, ne? :D
Miroslav Olšák | 10. 5. 2011 00:55:52
Velká cena 4b) byla nepokořena. Nechce-li se vám čekat na vzoráky, můžete ji zkusit vyřešit s hintem: Ramseyova věta říká, že pokud obarvíme hrany nekonečného úplněho grafu konečně mnoha barvami, pak bude existovat nekonečná jednobarevná klika (úplný podgraf).
Pepa T. | 10. 5. 2011 00:54:20
Ahojte,
Tam ta da dá, tímto uzavírám soutěž o velké ceny. Výsledky jsou na http://mks.mff.cuni.cz/velkeceny.php. Pokud se vám nechce čekat na vzorová řešení, nebo chcete k některým úlohám hinty, tažte se :). A komu se nezadařilo, nemusí plakat, brzy si zase dáme nějakou tlustou úlohu :).
Tam ta da dá, tímto uzavírám soutěž o velké ceny. Výsledky jsou na http://mks.mff.cuni.cz/velkeceny.php. Pokud se vám nechce čekat na vzorová řešení, nebo chcete k některým úlohám hinty, tažte se :). A komu se nezadařilo, nemusí plakat, brzy si zase dáme nějakou tlustou úlohu :).




