Chat Prasátek

Matematická sekce

<< < 1 2 ... 34 35 36 37 > >>

Alča | 4. 6. 2011 17:19:18

Tak jo, nejde. Nepochopila jsem přesně, co kalkulačka umí a co ne. (-:

Mirek Olšák | 4. 6. 2011 10:31:26

Coze? To vubec neumim.

Alča | 3. 6. 2011 23:40:45

Ještě jde 64.

Miroslav Olšák | 1. 6. 2011 23:59:17

Nejlip se zadani chape, kdyz mas v ruce tu kalkulacku. Da se to pochopit i tak, jak rikas, ale treba 4096 je na kalkulacce hodne tezke (oproti zavorkovani).

Tonda | 1. 6. 2011 16:00:37

chápu dobře zadání, že můžeme do toho výrazu doplnit závorky tak, aby vznikly požadované hodnoty?

Mirek Olšák | 31. 5. 2011 21:32:56

Já mám něco milého akorát s takovou tou kalkulačkou, která má tzv. "natural display". Umím v ní napsat výraz

$4^{2\frac12+2\frac12},$

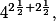
aby výsledek vyšel 4, 8, 16, 32, 128, 1024 nebo 4096. Umíte to taky?

Olin | 31. 5. 2011 18:20:21

Milovníci úprav výrazů a matematické analýzy si mohou rozmyslet, jak to dopadne, když bude Pepa do své pekelné skoroidentity přidávat další pětky.

Pepa T. | 31. 5. 2011 00:09:49

No jo, je to na -12tou... Pepa byl nějak mimo, když to psal :). Nemáte něco milého na rozveselení vy?

Miško | org | 30. 5. 2011 21:10:07

Hm, mne to vychadza 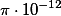$\pi\cdot10^{-12}$ ...

Pepa T. | 29. 5. 2011 20:48:03

Jojo, je to přesně tak, jak říká Kenny. Vnitřek je ve stupních. A podfuk je to pěkný :).

Petr | 29. 5. 2011 16:45:15

Tak to pak jo :-D

Kenny | 29. 5. 2011 16:32:16

Pepa má ve své ďábelské identitě asi na mysli, že vnitřek toho sinu je udán ve stupních. A je to teda pěkný podfuk :P

Petr | 29. 5. 2011 14:54:44

Tomu sinu s tím zlomkem 1/5 555 555 555 docela nevěřím, neuniká mi něco?

Kenny | 29. 5. 2011 14:35:58

Za to značení v trojce bych je fakt zabil :D. Prý S střed úsečky TV :D...

Pepa T. | 29. 5. 2011 14:20:22

Pětka je fakt ďábelská konstanta... To jste věděli, že

$\sin\left(\frac{1}{5555555555}\right) \doteq \pi \cdot 10^{-10}?$

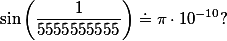
Kuba | 29. 5. 2011 14:19:01

Zadání MO na přístí rok je na internetu zde:http://skmo.sk/

Pepa T. | 25. 5. 2011 13:25:58

A na mathlinks (http://www.artofproblemsolving.com/Forum/view...) se objevila zadání polského celostátka! Můžete se podívat a udělat si srovnání :). Řešení jsou (v polštině) na (http://www.om.edu.pl/).

Pepa T. | 22. 5. 2011 23:41:27

Jinak Myšmaš byl letos fakt docela masakr... Smekám před všemi jedenácti hrdiny, kteří zvládli alespoň jednu úlohu vyřešit na alespoň čtyři body! Takhle náročný byl myšmaš naposledy před pěti lety (tj. ve 25. ročníku). Zájemcům doporučuju obzvláště tehdejší pětku a sedmičku ;).

Štěpán | 19. 5. 2011 18:32:45

jo, stačilo, děkuju

Pepa T. | 18. 5. 2011 23:43:38

Věnuju dokonce (byť schematický) popis řešení: Dokresli připsiště $E_b$ , $E_c$ trojúhelníka $ABC$ vzhledem k $B$ a $C$ a ukaž, že kružnice opsaná $PIQ$ je vlastně kružnicí opsanou $E_bIE_c$ (přímka $DE$ je chordála). A pak si už jen vzpomeň na Feuerbachovu kružnici :). Stačilo? Nebo ještě?

<< < 1 2 ... 34 35 36 37 > >>

Kontakt

email	info (zavináč) prase.cz
pošta	Matematický korespondenční seminář KAM MFF UK Malostranské náměstí 25 118 00 Praha 1

Organizátoři

Matematický korespondenční seminář je organizovaný studenty Matematicko-fyzikální fakulty UK pod záštitou Informatického ústavu UK a Oddělení propagace a mediální komunikace MFF UK.

Partneři

Realizace projektu byla podpořena Ministerstvem školství, mládeže a tělovýchovy

Matematický korespondenční seminář

Kalendář

Z naší fotogalerie

Kontakt

Organizátoři

Partneři