Kateřina Panešová | 14. 4. 2021 10:39:28
Dvojitá dávka čerstvých hintů k 3. jarní a 3. seriálové sérii!
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text 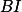 ,
, 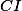 jsou výšky v trojúhelníku
jsou výšky v trojúhelníku 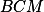 .
.
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text 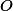 leží na
leží na 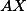 .+ skrytý text
.+ skrytý text 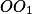 i
i 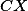 jsou kolmé na
jsou kolmé na 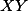 .
.
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 1.+ skrytý text
Rovnoramenný trojúhelník. + skrytý text
Úhel 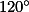 .
.
Úloha 2.+ skrytý text
Spočítej celkový počet stran trojúhelníků na obvodu n-úhelníku.
Úloha 3.+ skrytý text
Uvaž trojúhelníky o straně dva.
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Vyúhli, že trojúhelníky 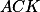 a
a 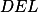 jsou shodné.+ skrytý text
jsou shodné.+ skrytý text
Využij úsekové úhly.
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Dokresli 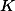 průsečík
průsečík 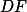 a
a 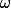 .+ skrytý text
.+ skrytý text
Trojúhelníky 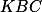 a
a 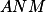 jsou podobné s SUS.
jsou podobné s SUS.
Úloha 8.+ skrytý text
Počítejte obsah doplňku trojúhelníku 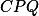 vzhledem ke kosočtverci
vzhledem ke kosočtverci 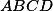 .+ skrytý text
.+ skrytý text
Ukažte, že hledaná nezávislost je ekvivalentní tomu, že hodnota 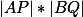 nezávisí na poloze
nezávisí na poloze  .+ skrytý text
.+ skrytý text
Překlopte body  ,
, 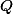 podle úsečky
podle úsečky 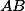 na body
na body 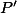 ,
, 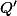 .+ skrytý text
.+ skrytý text
Ukažte, že body  ,
, 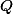 ,
, 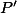 ,
, 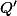 a střed
a střed 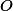 kosočtverce
kosočtverce 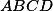 leží na jedné kružnici.+ skrytý text
leží na jedné kružnici.+ skrytý text 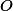 je Švrčkův bod trojúhelníku
je Švrčkův bod trojúhelníku 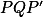 .+ skrytý text
.+ skrytý text
Nezávislost prokažte pomocí mocnosti z  .
.
Úloha 1.+ skrytý text
Nejprve vyřeš prvočíselné mocniny, potom použij Čínskou zbytkovou větu.
Úloha 2.+ skrytý text
Zkus jako prvky krutopřísné posloupnosti použít 1 a prvočíslo p.+ skrytý text
Pro důkaz ireducibility se na to podívej mod p.
Úloha 3.+ skrytý text
3. Zvol 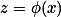 .+ skrytý text
.+ skrytý text
Použij 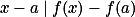 .
.
Dominik Stejskal | 13. 3. 2021 23:37:52
Nové hinty ke druhé jarní sérii jistě pomůžou rozbít i ty odolnější úlohy...
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Co umíš říct o 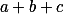 ?
?
Úloha 2. + skrytý text
Šimpanzovi naproti Radečkovi dej co nejvíce banánů.
Úloha 3. + skrytý text
Rozlož povrch čtyřstěnu na síť. + skrytý text
Nahlédni, že Pavel si nepomůže přecházením přes více hran.
Úloha 4. + skrytý text
Rozdíl základů pátých mocnin by musel dělit  .
.
Úloha 5. + skrytý text
V kolika takových dvojicích je na začátku každá karta?
Úloha 6. + skrytý text
Počítej modulo 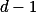 .
.
Úloha 7. + skrytý text
Čísla lze vydělit jejich společným dělitelem. + skrytý text
Dívej se na čísla modulo 2. Co se stane po dvou krocích?
Úloha 8. + skrytý text
Vyhovují právě dvojice splňující 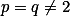 . + skrytý text
. + skrytý text
Zkoumej řád 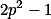 modulo
modulo 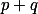 .
.
Lenka Kopfová | 25. 2. 2021 18:42:36
Ahoj,
pokud chceš potrénovat před celostátkem nebo si jen započítat pro radost je zde nová série TRiKSka http://iksko.org/triks/current.php. Pokud nevíš, co je TRiKS, můžeš se kouknout do pravidel pro bližší info http://iksko.org/triks/pravidla.pdf. Navíc máme exkluzivní nabídku - vítěz každého dalšího TRiKS získá TRiKS šátek!
pokud chceš potrénovat před celostátkem nebo si jen započítat pro radost je zde nová série TRiKSka http://iksko.org/triks/current.php. Pokud nevíš, co je TRiKS, můžeš se kouknout do pravidel pro bližší info http://iksko.org/triks/pravidla.pdf. Navíc máme exkluzivní nabídku - vítěz každého dalšího TRiKS získá TRiKS šátek!
Lenka Kopfová | 23. 2. 2021 14:50:01
Řešení 9:
+ skrytý text
Uvažujme stejnolehlosti z bodů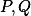 , které zobrazují
, které zobrazují 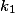 resp.
resp. 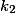 na
na 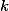 . První stejnolehlost zobrazuje
. První stejnolehlost zobrazuje 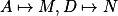 a druhá zobrazuje
a druhá zobrazuje 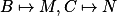 . Tedy platí
. Tedy platí 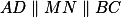 . Dále si všimněme, že
. Dále si všimněme, že 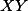 je chordála kružnic
je chordála kružnic 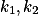 , tedy
, tedy 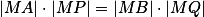 , takže
, takže 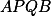 je tětivový. Obdobně i
je tětivový. Obdobně i 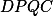 je tětivový. Odtud
je tětivový. Odtud 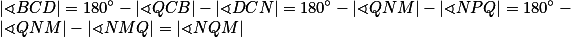 . Jinak řečeno
. Jinak řečeno 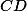 je tečna
je tečna 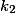 (tedy i ke
(tedy i ke 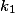 ) a obdobně
) a obdobně 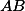 je společná tečna
je společná tečna 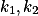 . Takže
. Takže 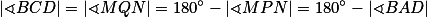 , tedy
, tedy 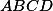 je tětivový, navíc
je tětivový, navíc 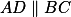 , takže se jedná o rovnoramenný lichoběžník a
, takže se jedná o rovnoramenný lichoběžník a 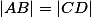 .
.
10:
Dokaž, že pro každé přirozené číslo platí:
platí:
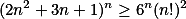
+ skrytý text
Uvažujme stejnolehlosti z bodů
10:
Dokaž, že pro každé přirozené číslo
šimon | 22. 2. 2021 14:03:57
Dobrý den, potřeboval bych vypočítat tento příklad i s řešením: Jestliže zvětšíme jednu stranu čtverce o 20 cm a sousední stranu zmenšíme o 6 cm, dostaneme rozměry obdélníku, který má obsah 1,4krát větší než obsah původního čtverce. Určete délku jeho strany. Předem děkuji. Počítání s kvadratickými rovnicemi
Kateřina Panešová | 11. 2. 2021 12:50:13
Ahoj! Čeká na vás dvojitá várka hintů, a to k 1. jarní a 2. seriálové sérii!
1. jarní série
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Ůloha 7.+ skrytý text
Úloha 8.+ skrytý text
2. seriálová série
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
1. jarní série
Úloha 1.+ skrytý text
Všichni mají stejnou pravdomluvnost.
Úloha 2.+ skrytý text
Přelož si všechna tvrzení mudrců do tvaru "je mezi námi tolik a tolik pravdomluvců".
Úloha 3.+ skrytý text
Zkus nejdřív menší čtverec 5x5.
Úloha 4.+ skrytý text
Nahlédni, že celá trasa paprsku musí být středově souměrná. + skrytý text
Jaký bod je potom přesně v polovině trasy?
Úloha 5.+ skrytý text
Můžou vedle sebe sedět dva kluci? + skrytý text
Jaké posloupnosti dívek a chlapců lze sestavit? + skrytý text
Podívej se na to modulo 3.
Úloha 6.+ skrytý text
Pro sudá n využij 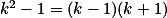 . + skrytý text
. + skrytý text
Pro lichá n se podívej modulo 8 na sudá a, b.
Ůloha 7.+ skrytý text
Ukaž, že pro 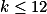 dokáže Pavel vybrat všechny pěšce. + skrytý text
dokáže Pavel vybrat všechny pěšce. + skrytý text
Důkaz sporem a Dirichletův princip.
+ skrytý textNajdi konstrukci pro 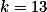 .
.
Úloha 8.+ skrytý text
Vyjde, že takové  existuje.
existuje.
+ skrytý text
+ skrytý text
Uvažuj 2021 záhadných čísel tvaru 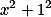 až
až 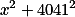 .
.
+ skrytý text
+ skrytý text
Abys zajistil/a nesoudělnost, vzpomeň si na úlohy s hledáním čísla nesoudělného s nějakými malými čísly, kde jde zvolit faktoriál malých čísel + 1.+ skrytý text
+ skrytý text
Zvol 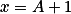 , kde
, kde 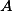 je liché a dělitelné všemi lichými čísly od
je liché a dělitelné všemi lichými čísly od 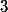 do
do 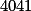 .
.
+ skrytý text
Následně ukaž, že pro libovolné sudé číslo tvaru 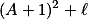 mezi nimi už musí být
mezi nimi už musí být 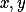 splňující
splňující 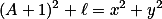 soudělná.
soudělná.
+ skrytý text
+ skrytý text
+ skrytý text
Pro 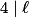 se stačí podívat na rovnici modulo
se stačí podívat na rovnici modulo 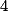 .
.
+ skrytý text
Pro 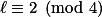 by stačilo, aby existovalo prvočíslo
by stačilo, aby existovalo prvočíslo  tvaru
tvaru 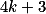 , které dělí
, které dělí 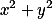 . Potom totiž
. Potom totiž  dělí jak
dělí jak  , tak
, tak 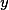 . Jak najít takové
. Jak najít takové  ?
?
+ skrytý text
+ skrytý text
V tomto případě existuje něco, co je určitě tvaru 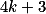 . Pak stačí zvolit libovolné prvočíslo tvaru
. Pak stačí zvolit libovolné prvočíslo tvaru 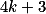 , které dělí to něco.
, které dělí to něco.
+ skrytý text
+ skrytý text
Konkrétně 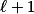 je tvaru
je tvaru 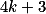 . Tedy už stačí jen zajistit, aby
. Tedy už stačí jen zajistit, aby  dělilo
dělilo 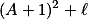 . Jak můžeme definovat
. Jak můžeme definovat 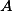 , aby to bylo splněno?
, aby to bylo splněno?
+ skrytý text
+ skrytý text
Ukaž, že 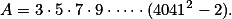 vyhovuje.
vyhovuje.
2. seriálová série
Úloha 1.+ skrytý text
Použij malou Fermatovu větu. + skrytý text
V druhé kongruenci umocni na druhou a získej 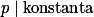 .
.
Úloha 2.+ skrytý text
Fundamentální jednotka je 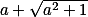 . + skrytý text
. + skrytý text 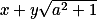 bude její mocninou se sudým exponentem. + skrytý text
bude její mocninou se sudým exponentem. + skrytý text
Rozepiš binomickou větu a posbírej racionální členy -- skoro všechny jsou násobky 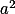 .
.
Úloha 3.+ skrytý text
Dívej se v 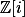 a rozmysli si, že
a rozmysli si, že 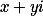 je
je 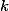 -tá mocnina. + skrytý text
-tá mocnina. + skrytý text
Interpretuj podmínku 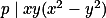 jako multiplikativní množinu v
jako multiplikativní množinu v 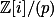 . + skrytý text
. + skrytý text
Tato multiplikativní množina má 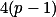 prvků, zatímco
prvků, zatímco 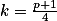 .
.
Dominik Stejskal | 15. 1. 2021 01:06:53
Nový rok přináší spoustu zajímavých věcí, jako třeba hinty ke 4. podzimní sérii! :)
Úloha 1. + skrytý text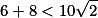 ,
,
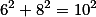 .
.
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Podívej se na dvojici s minimální vzdáleností. + skrytý text
Buď je některý zasažen dvakrát, nebo je můžeš odebrat.
Úloha 3. + skrytý text
Kolik červených bodů může být ve vzdálenosti přesně 1 od jednoho daného červeného bodu?
Úloha 4. + skrytý text
Dokresli si středy úseček 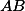 a
a 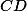 a úhlením hledej podobné (a shodné) trojúhelníky.
a úhlením hledej podobné (a shodné) trojúhelníky.
Úloha 5. + skrytý text
Body 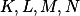 leží na ose
leží na ose 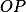 . + skrytý text
. + skrytý text
Úhly 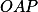 a
a 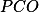 se rovnají. Ukaž, že kružnice
se rovnají. Ukaž, že kružnice 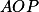 a
a 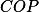 mají stejný poloměr.
mají stejný poloměr.
Úloha 6. + skrytý text
Uvažuj všech 100 rotací, které zobrazí 100-úhelník na sebe. + skrytý text
Kolikrát se zobrazí modrý vrchol na červený?
Úloha 7. + skrytý text
Dokresli bod 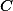 překlopený přes
překlopený přes 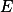 . + skrytý text
. + skrytý text
Přenášej délky pomocí rovnoběžek a kolmic.
Úloha 8. + skrytý text
Odhadni dvěma způsoby počet rovnoramenných trojúhelníků.
Kateřina Panešová | 9. 12. 2020 23:31:55
HINTY! Nevěděl/a sis rady s některou z úloh 3. podzimní a 1. seriálové série? Dej jí ještě jednu šanci!
3. podzimní série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
1. seriálová série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
3. podzimní série
Úloha 1. + skrytý text
Dej kouli do středu stolu, pak už to jde samo...
Úloha 2. + skrytý text
Nechť je 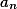 minimální počet soutěžících, který je potřeba, aby celkový vítěz měl
minimální počet soutěžících, který je potřeba, aby celkový vítěz měl  výher. Najdi rekurenci pro
výher. Najdi rekurenci pro 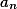 .+ skrytý text
.+ skrytý text
Jsou to Fibonacciho čísla.
Úloha 3. + skrytý text
Uprav na společného jmenovatele a dívej se na dělitelnost 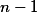 .
.
Úloha 4. + skrytý text
Všimni si, že pro 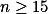 je na šachovnici víc než 111 mincí. Co
je na šachovnici víc než 111 mincí. Co 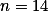 ? A co
? A co 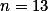 ?+ skrytý text
?+ skrytý text
Pro 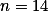 je počet mincí sudý.+ skrytý text
je počet mincí sudý.+ skrytý text
Najdi konstrukci pro 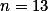 .
.
Úloha 5. + skrytý text
Substituuj 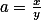 ,
, 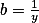 .+ skrytý text
.+ skrytý text
Dostaneš lineární lomený výraz v  , zatímco podmínka omezuje
, zatímco podmínka omezuje  na nějaký interval.
na nějaký interval.
Úloha 6. + skrytý text
Je to 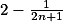 .+ skrytý text
.+ skrytý text
Vezmi silnici s limitem 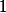 a odhadni tím průměry dvojic silnic z krajních měst do nějakého třetího.
a odhadni tím průměry dvojic silnic z krajních měst do nějakého třetího.
Úloha 7. + skrytý text
Dej rovničku do tvaru 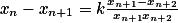 , vynásob všechny tyhle věci přes všechna
, vynásob všechny tyhle věci přes všechna  a použij racionalitu
a použij racionalitu 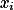 .
.
Úloha 8. + skrytý text
Dokresli O opsiště ABC.+ skrytý text
Trojúhelníky 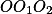 jsou podobné nezávisle na P.
jsou podobné nezávisle na P.
1. seriálová série
Úloha 1. + skrytý text
Zkus mod 3, anebo trikový rozklad 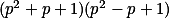 .
.
Úloha 2. + skrytý text
Nechť je 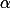 kořenem
kořenem 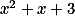 . Dokaž, že
. Dokaž, že ![\textstyle \zet[\alpha] \textstyle \zet[\alpha]](https://prase.cz/chat/texmaker.php?tex=%5Ctextstyle+%5Czet%5B%5Calpha%5D&hash=455fdaa03c62848cf3af) je eukleidovský, rozlož a použij tvrzení o mocninách.
je eukleidovský, rozlož a použij tvrzení o mocninách.
Úloha 3. + skrytý text
3. Uprav na čtverec + čtverec = čtverec + 1, poté využij vztahů prvočíselného rozkladu čísla a možností jeho vyjádření jako čtverec + čtverec.
Dominik Stejskal | 14. 11. 2020 20:31:54
Hinty jsou zpět! S nimi už zbytek druhé podzimní série snadno rozlouskneš.
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Podívej se na osovou souměrnost podle kolmice k 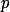 . Vhodně zvol
. Vhodně zvol 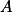 ,
, 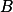 ,
, 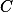 .
.
Úloha 2. + skrytý text
Co kdyby Terka začínala na úhlopříčce?
Úloha 3. + skrytý text
Hledej pravoúhlé trojúhelníky. + skrytý text
Opiš 2020-úhelníku kružnici, použij Thaletovu a Pythagorovu větu.
Úloha 4. + skrytý text
Sečti všechny rovnice. + skrytý text
Uprav na součiny a využij 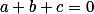 .
.
Úloha 5. + skrytý text
Dokresli překlopení 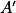 bodu
bodu 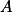 přes osu úsečky
přes osu úsečky 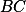 .
.
Úloha 6. + skrytý text
Označ si průsečík úseček 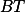 a
a 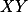 a hledej podobné trojúhelníky.
a hledej podobné trojúhelníky.
Úloha 7. + skrytý text
Vezmi diagonálu, domy mimo ní popáruj symetricky a domy na ní vyřeš zvlášť.
Úloha 8. + skrytý text
Lichý cyklus neexistuje právě tehdy, když jdou letiště obarvit dvěma barvami tak, aby každá dvě spojená letiště měla různou barvu. + skrytý text
Pro sudá n může libovolný z hráčů zařídit, že těsně před koncem hry bude stejně letišť od každé z těchto dvou barev.
Václav Janáček | org | 9. 8. 2020 12:56:52
Samozřejmě máme ukázat 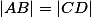 , ale jinak skoro dobře :D
, ale jinak skoro dobře :D
Václav Janáček | org | 7. 8. 2020 14:30:13
Řešení 8:
+ skrytý text
9:
Nechť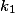 ,
, 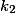 jsou kružnice protínající se v bodech
jsou kružnice protínající se v bodech 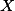 ,
, 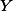 . Nechť s nimi kružnice
. Nechť s nimi kružnice 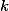 svírá vnitřní dotek postupně v bodech
svírá vnitřní dotek postupně v bodech 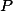 ,
, 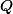 . Nechť
. Nechť 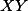 protíná
protíná 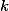 v bodech
v bodech 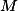 a
a 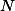
Polopřímky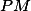 a
a 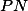 protínají
protínají 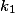 postupně v
postupně v 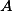 a
a 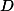 . Obdobně polopřímky
. Obdobně polopřímky 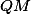 a
a 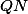 protnou
protnou 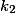 v
v 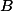 a
a 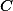 . Ukažte
. Ukažte 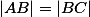 .
.
+ skrytý text
Ukáži, že je to 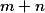 . Nejdříve předpokládejme, že existuje šachovnice, na kterou je možno umístit víc věží. Vezměme nejmenší takovou šachovnici (nejmenší
. Nejdříve předpokládejme, že existuje šachovnice, na kterou je možno umístit víc věží. Vezměme nejmenší takovou šachovnici (nejmenší 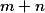 ). BÚNO nechť
). BÚNO nechť 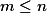 . Poté jsou v některém řádku více než
. Poté jsou v některém řádku více než 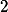 věže, jinak jich je nejvýše
věže, jinak jich je nejvýše 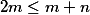 .
.
Vyberme některou z nekrajních věží v tomto řádku. Ta ohrožuje jednu věž vlevo a jednu vpravo. Musí být tedy ve sloupci sama. Odstraněním tohoto sloupce získáme menší tabulku s více než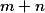 věžemi, přitom stále každá věž zjevně ohrožuje právě dvě jiné. Spor.
věžemi, přitom stále každá věž zjevně ohrožuje právě dvě jiné. Spor.
Rozmístění věží do celého levého sloupce, celého spodního řádku a na políčko vpravo nahoře je platné rozmístění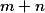 věží.
věží.
Vyberme některou z nekrajních věží v tomto řádku. Ta ohrožuje jednu věž vlevo a jednu vpravo. Musí být tedy ve sloupci sama. Odstraněním tohoto sloupce získáme menší tabulku s více než
Rozmístění věží do celého levého sloupce, celého spodního řádku a na políčko vpravo nahoře je platné rozmístění
9:
Nechť
Polopřímky
Josef Minařík | org | 28. 7. 2020 20:46:36
Řešení 7:
+ skrytý text
8.
Kolik nejvíce šachových věží je možné umístit na šachovnici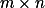 , kde
, kde 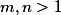 , tak, aby každá věž ohrožovala právě dvě další? Dvě věže se navzájem ohrožují, pokud jsou ve stejném sloupci nebo řádku a není mezi nimi žádná jiná věž.
, tak, aby každá věž ohrožovala právě dvě další? Dvě věže se navzájem ohrožují, pokud jsou ve stejném sloupci nebo řádku a není mezi nimi žádná jiná věž.
+ skrytý text
Nejprve si všimněme, že pokud 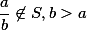 , potom
, potom 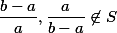 , protože
, protože 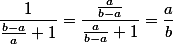 . Dále předpokládejme, že
. Dále předpokládejme, že 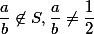 a
a 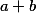 je minimální. To je ovšem spor, protože jeden ze zlomků
je minimální. To je ovšem spor, protože jeden ze zlomků 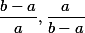 je menší než 1, není v
je menší než 1, není v 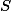 , a má menší součet čitatele a jmenovatele. Tím jsme dokázali, že neexistuje uvažovaný zlomek
, a má menší součet čitatele a jmenovatele. Tím jsme dokázali, že neexistuje uvažovaný zlomek 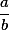 , a úloha je vyřešena.
, a úloha je vyřešena.
8.
Kolik nejvíce šachových věží je možné umístit na šachovnici
Michal Janík | org | 24. 7. 2020 10:55:39
Řešení 6:
+ skrytý text
7.
Množina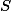 , která obsahuje jen racionální čísla má následující vlastnosti:
, která obsahuje jen racionální čísla má následující vlastnosti:
a)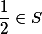
b) Pokud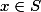 , tak
, tak 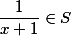 a
a 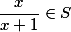 .
.
Dokažte, že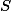 obsahuje všechna racionální čísla z intervalu
obsahuje všechna racionální čísla z intervalu 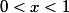 .
.
+ skrytý text
Pro nenulové 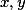 vydělíme celou nerovnost kladným výrazem
vydělíme celou nerovnost kladným výrazem 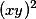 a zavedeme si funkci
a zavedeme si funkci 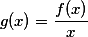 , čímž dostaneme
, čímž dostaneme 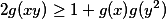 . Dosazením
. Dosazením 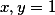 dostaneme
dostaneme 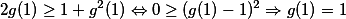 . Dosazením
. Dosazením 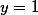 dostaneme
dostaneme 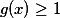 . Naposledy dosazením
. Naposledy dosazením 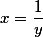 dostaneme
dostaneme 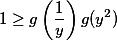 , ale protože platí
, ale protože platí 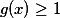 , musí platit také
, musí platit také 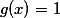 . Z toho plyne
. Z toho plyne 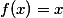 , což zkouškou lehce ověříme.
, což zkouškou lehce ověříme.
7.
Množina
a)
b) Pokud
Dokažte, že
Zdeněk Pezlar | org | 21. 7. 2020 20:20:39
Řešení 5:
+ skrytý text
Pokud označíme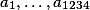 prvky naší množiny a
prvky naší množiny a  jejich součet, pak
jejich součet, pak 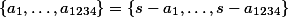 . Tyto množiny jsou shodné a obě mají právě
. Tyto množiny jsou shodné a obě mají právě 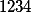 různých prvků, tedy součet prvků obou množin bude shodný:
různých prvků, tedy součet prvků obou množin bude shodný: 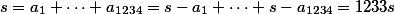 , tedy
, tedy 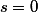 , máme tedy
, máme tedy 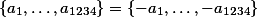 . Pokud by jedno z čísel bylo nulové, například
. Pokud by jedno z čísel bylo nulové, například 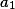 , tak
, tak 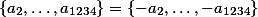 , součin
, součin 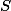 prvků obou množin bude shodný,
prvků obou množin bude shodný, 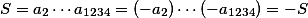 , jedno z
, jedno z 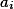 je
je 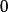 , spor s růzností čísel. Můžeme proto čísla rozdělit na
, spor s růzností čísel. Můžeme proto čísla rozdělit na 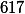 dvojic
dvojic 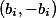 pro nenulová
pro nenulová 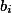 . Součin všech čísel bude
. Součin všech čísel bude 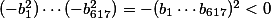 .
.
6.
Určete všechny funkce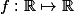 , které splňují
, které splňují 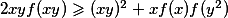 pro všechna reálná
pro všechna reálná 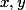 .
.
+ skrytý text
Pokud označíme
6.
Určete všechny funkce
Josef Minařík | org | 16. 7. 2020 23:07:19
Řešení 4:
+ skrytý text
5. Množina 1234 (různých) reálných čísel má následující vlastnost. Když nahradíme každé číslo množiny součtem zbývajících 1233 čísel, dostaneme stejnou množinu 1234 čísel. Dokažte, že součin těchto 1234 čísel je záporný.
+ skrytý text
Ukážeme, že 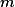 může být nejvýše
může být nejvýše 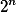 . Uvažujme nějakou vyhovující tabulku, nejmenší číslo v každém sloupci je BÚNO 0 (jinak můžeme čísla v daném sloupci posunout), potom žádné číslo nemůže být větší než 1. Pokud je někde v tabulce číslo větší než 0 a menší než 1, můžeme místo něj napsat 0 a tabulka bude pořád splňovat podmínku ze zadání. Stačí nám tedy uvažovat tabulky vyplněné 0 a 1. Pokud by ovšem tabulka měla více než
. Uvažujme nějakou vyhovující tabulku, nejmenší číslo v každém sloupci je BÚNO 0 (jinak můžeme čísla v daném sloupci posunout), potom žádné číslo nemůže být větší než 1. Pokud je někde v tabulce číslo větší než 0 a menší než 1, můžeme místo něj napsat 0 a tabulka bude pořád splňovat podmínku ze zadání. Stačí nám tedy uvažovat tabulky vyplněné 0 a 1. Pokud by ovšem tabulka měla více než 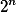 řádků, budou některé dva řádky stejné, což je spor se zadáním.
řádků, budou některé dva řádky stejné, což je spor se zadáním.
Tabulka, jejíž řádky jsou všechny možné posloupnosti 0 a 1, zřejmě vyhovuje zadané podmínce a má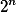 řádků.
řádků.
Tabulka, jejíž řádky jsou všechny možné posloupnosti 0 a 1, zřejmě vyhovuje zadané podmínce a má
5. Množina 1234 (různých) reálných čísel má následující vlastnost. Když nahradíme každé číslo množiny součtem zbývajících 1233 čísel, dostaneme stejnou množinu 1234 čísel. Dokažte, že součin těchto 1234 čísel je záporný.
Magdaléna Mišinová | org | 12. 7. 2020 20:07:24
Řešení 3:
+ skrytý text
Protože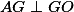 ,
, 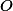 je střed
je střed 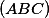 a
a 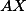 je tětiva této kružnice, tak
je tětiva této kružnice, tak 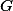 je střed
je střed 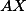 .
.
Označme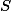 střed
střed 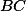 . Víme, že
. Víme, že 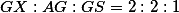 . Těžiště vždy leží uvnitř trojúhelníku, takže
. Těžiště vždy leží uvnitř trojúhelníku, takže 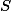 je střed
je střed 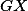 . Tím jsme dokázali, že úsečky
. Tím jsme dokázali, že úsečky 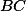 a
a 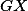 se navzájem půlí, takže čtyřúhelník
se navzájem půlí, takže čtyřúhelník 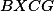 je rovnoběžník.
je rovnoběžník.
Platí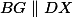 a
a 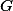 je střed
je střed 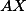 , takže
, takže 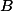 je střed
je střed 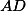 . Obdobně
. Obdobně 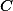 je střed
je střed 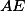 . Opsiště
. Opsiště 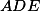 zkonstruujeme proto tak, že z bodů
zkonstruujeme proto tak, že z bodů 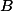 a
a 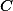 vedeme kolmice postupně na
vedeme kolmice postupně na 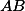 a
a 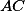 . Proto body
. Proto body 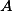 ,
, 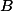 ,
, 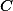 a opsiště
a opsiště 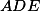 určitě leží na kružnici, jak jsme chtěli.
určitě leží na kružnici, jak jsme chtěli.
4. Mějme přirozené číslo . V závislosti na
. V závislosti na  najděte největší
najděte největší 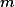 s následující vlastností. Tabulka s
s následující vlastností. Tabulka s 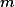 řádky a
řádky a  sloupci můžeme být vyplněna reálnými čísly tak, aby pro každé dva řádky, čísla v nichž si označíme
sloupci můžeme být vyplněna reálnými čísly tak, aby pro každé dva řádky, čísla v nichž si označíme 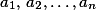 a
a 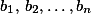 , platilo:
, platilo:
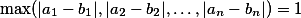
+ skrytý text
Protože
Označme
Platí
4. Mějme přirozené číslo
Zdeněk Pezlar | org | 12. 7. 2020 17:52:47
Řešení 2:
+ skrytý text
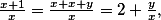 takže pokud označíme
takže pokud označíme 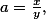 , tak díky AG a Cauchymu platí:
, tak díky AG a Cauchymu platí:
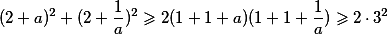 a jsme doma.
a jsme doma.
3. V trojúhelníku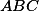 s opsištěm
s opsištěm 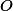 a těžištěm
a těžištěm 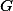 platí
platí 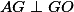 . Označme
. Označme 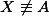 druhý průsečík
druhý průsečík 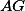 s kružnicí
s kružnicí 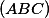 a mějme
a mějme 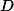 průsečík přímek
průsečík přímek 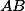 a
a 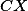 ,
, 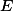 průsečík
průsečík 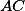 a
a 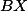 . Ukaž, že opsiště
. Ukaž, že opsiště 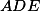 leží na
leží na 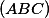 .
.
+ skrytý text
3. V trojúhelníku
Huu Quy Nguyen | 12. 7. 2020 15:03:08
Řešení:
+ skrytý text
Dokážeme matematickou indukcí :)
Pro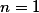 tvrzení zřejmě platí.
tvrzení zřejmě platí.
Předpokládejme, že tvrzení platí pro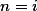 .
.
Pak z indukčního předpokladu platí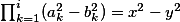 pro celá
pro celá 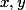 .
.
Nyní pro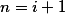 platí
platí 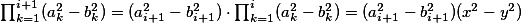
Jenže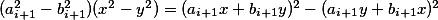 , což je rozdíl dvou čtverců, čímž jsme hotovi.
, což je rozdíl dvou čtverců, čímž jsme hotovi.
2. Pro kladná reálná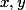 platí
platí 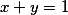 . Dokaž, že platí
. Dokaž, že platí 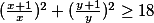
+ skrytý text
Dokážeme matematickou indukcí :)
Pro
Předpokládejme, že tvrzení platí pro
Pak z indukčního předpokladu platí
Nyní pro
Jenže
2. Pro kladná reálná
Fíla | org | 11. 7. 2020 22:51:48
Ahoj,
jelikož je ti určitě smutno, že už tento rok skončily prasečí série, nechceš zakrnět, a proto by sis rád vyřešil nějaké úložky navíc. Proto bychom rádi obnovili prasečí maraton.
Pravidla jsou následující. Vždy když vyřešíš nejnovější úlohu, napíšeš její řešení a hned zadáš další. Nějací orgové se určitě připojí také, když se budou moc nudit ;) (prosím abyste řešení dávali formou skrytého textu, aby si ji i ostatní mohli vyřešit a hned neviděli řešení).
1.
Dokažte, že pro libovolná přirozená čísla ,
, 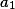 ,
, 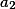 ,
, 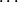 ,
, 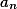 ,
,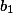 ,
, 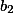 ,
, 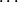 ,
, 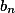 je možné zapsat součin
je možné zapsat součin 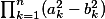 jako rozdíl dvou čtverců (celých čísel).
jako rozdíl dvou čtverců (celých čísel).
jelikož je ti určitě smutno, že už tento rok skončily prasečí série, nechceš zakrnět, a proto by sis rád vyřešil nějaké úložky navíc. Proto bychom rádi obnovili prasečí maraton.
Pravidla jsou následující. Vždy když vyřešíš nejnovější úlohu, napíšeš její řešení a hned zadáš další. Nějací orgové se určitě připojí také, když se budou moc nudit ;) (prosím abyste řešení dávali formou skrytého textu, aby si ji i ostatní mohli vyřešit a hned neviděli řešení).
1.
Dokažte, že pro libovolná přirozená čísla
Olin | org | 8. 6. 2020 01:40:58
Na krajská kola MO B+C už se dá i registrovat:
https://mo.mff.cuni.cz/bc/
https://mo.mff.cuni.cz/bc/