Denisa Hanušková | org | 8. 2. 2023 17:39:30
Ahoj, s koncem serií se k Vám blíží další hinty. Zde jsou:
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 1.+ skrytý text
Dívej se na rozdíly sousedních průměrů.
Úloha 2.+ skrytý text
Popáruj dělitele 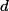 s
s 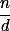 .
.
Úloha 3.+ skrytý text
Zprůměruj první a třetí nejvyšší a redukuj postupně dolů. Pro číslo 1000 opakuj postup z obou stran.
Úloha 4.+ skrytý text
Popáruj podmnožiny, které obsahují svůj aritmetický průměr s těmi, který jej neobsahují.
Úloha 5.+ skrytý text
Rozděl čísla na sudá a lichá.
Úloha 6.+ skrytý text
Spočítej 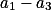
Úloha 7.+ skrytý text
Rozmysli si, že 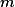 se nezvětšuje.
se nezvětšuje.
Úloha 8.+ skrytý text
Více, než 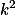 jich být nemůže, takže každá trojice, která může být pěkná, musí.+ skrytý text
jich být nemůže, takže každá trojice, která může být pěkná, musí.+ skrytý text
Uspořádej si reálná čísla podle velikosti. Podívej se na vzdálenosti 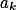 a
a 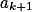 . Jak pak musí vypadat ostatní mezery?
. Jak pak musí vypadat ostatní mezery?
Úloha 1. + skrytý text
Fíla skutečně mohl takovou množinu najít.+ skrytý text
Zkus nějakou množinu bez okraje.
Úloha 2. + skrytý text
Postupně přidávej body z konvexního obalu, když to je potřeba, tak dva najednou.+ skrytý text
Přidávej body tak, aby poslední dvě písmena napsaného textu byla stejná.
Úloha 3. + skrytý text
Uvaž libovolný bod na povrchu mnohostěnu a zobraz mnohostěn ve stejnolehlosti se středem v tomto bodě a koeficientem 3/4.+ skrytý text
Použij nekonečnou Hellyho větu.+ skrytý text
Libovolné 4 obrazy se protínají v těžišti příslušného čtyřstěnu.
Áďa | org | 10. 1. 2023 11:17:38
Ahojky, už určitě netrpělivě očekáváš hintíky 4. podzimní série. Mám pro Tebe dobrou zprávu! Už nemusíš čekat déle!
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Jaké dvojice můžou vzniknout při prvním rozdělení? A při druhém?
Úloha 2. + skrytý text
Čtvrté číslo zvol co nejvyšší.
Úloha 3. + skrytý text
Za jak dlouho alespoň někdo ví vše?
Úloha 4. + skrytý text
Jak musí vypadat graf, kde je mezi dvěma týmy hrana, právě když spolu hrály v některém z prvních dvou dnů?
Úloha 5. + skrytý text
Ukaž, že pokud je 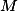 město, do kterého doletí nejvíc letadel, a
město, do kterého doletí nejvíc letadel, a  ,
,  nějaká jiná města, ze kterých letí letadla do
nějaká jiná města, ze kterých letí letadla do 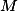 , pak úhel
, pak úhel 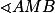 musí být vyšší než
musí být vyšší než 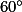 .
.
Úloha 6. + skrytý text
Smaž právě jednu šipku mezi každými dvěma týmy. + skrytý text
Rozděl si to na dvojice, kde pokaždé vyhrál jiný tým, a na ty zbylé.
Úloha 7. + skrytý text
Využij faktu, že počet přijatých GIFů je stejný jako počet odeslaných, k dokázání 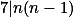 . Najdi konstrukci pro vyhovující
. Najdi konstrukci pro vyhovující 
Úloha 8. + skrytý text
Indukcí. Rozděl si maximální kliky podle toho, jak vznikly z menšího grafu.
Zdeněk Pezlar | org | 29. 12. 2022 19:27:13
Ahoj,
chceš trochu potrénovat před blížícím se krajským kolem Matematické olympiády A? Potom je tu právě pro tebe TRiKSko -- tréninková online soutěž semináře iKS. Bližší informace najdeš na https://iksko.org/triks/current.php.
chceš trochu potrénovat před blížícím se krajským kolem Matematické olympiády A? Potom je tu právě pro tebe TRiKSko -- tréninková online soutěž semináře iKS. Bližší informace najdeš na https://iksko.org/triks/current.php.
Denisa Hanušková | org | 6. 12. 2022 20:37:09
Ahoj, stále se trápíš nad některou z úloh? Pak Tě jistě potěší pozdní dárek od Mikuláše, který Ti u nás v podobě hintů zanechal.
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
+ skrytý text
Úloha 7. + skrytý text
+ skrytý text
Úloha 8. + skrytý text
+ skrytý text
Úloha 1.+ skrytý text
+ skrytý text
Úloha 2. + skrytý text
+ skrytý text
Úloha 3. + skrytý text
+ skrytý text
Úloha 1. + skrytý text
Vypiš si, jaká prvočísla spolu mohou sousedit.
Úloha 2. + skrytý text
Zvol za  postupně
postupně 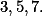
Úloha 3. + skrytý text
Pokrať 19, rozlož na součin.
Úloha 4. + skrytý text
Podívej se na paritu.
Úloha 5. + skrytý text
V posloupnosti 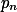 se od nějaké chvíle bude opakovat
se od nějaké chvíle bude opakovat 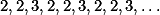
Úloha 6. + skrytý text
Označ si ony čtverce 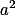 a
a 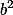 ,pak odečti a faktorizuj.
,pak odečti a faktorizuj.
+ skrytý text
Odhadni 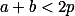
Úloha 7. + skrytý text
Faktorizuj 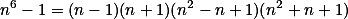
+ skrytý text
Vyjádři 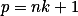 , dosaď a rozeber případy podle toho, kterou závorku
, dosaď a rozeber případy podle toho, kterou závorku  dělí.
dělí.
Úloha 8. + skrytý text
Přepiš na součin kombinačních čísel.
+ skrytý text
Přidej k součinům  , abys dostal kombinační čísla s
, abys dostal kombinační čísla s 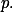
Úloha 1.+ skrytý text
Nemusí.
+ skrytý text
Protipříklad je i na čtyřech vrcholech.
Úloha 2. + skrytý text
Extremální princip.
+ skrytý text
Dívej se na úhly.
Úloha 3. + skrytý text
Udělej strom na triangulaci.
+ skrytý text
Hledej vrchol, co je "uprostřed".
Zdeněk Pezlar | org | 22. 11. 2022 13:06:52
Ahoj!
Již tradiční internetová soutěž Mathrace (http://brkos.math.muni.cz/mathrace/)
proběhne už za týden v úterý 30.11.! Soutěž je určena pro nejvýše čtyřčlenné týmy středoškoláků, pro nadšence mimo střední školu je tu kategorie Underground. Soutěž organizují studenti Přf MUNI.
Čím se liší Mathrace od jiných matematických soutěží? Na řešení úloh jsou povolené libovolné zdroje - kalkulačky, Geogebra, WolframAlpha, programování - můžete si proto být jistí, že i s pomocí těchto nástrojů budete muset nad úlohami přemýšlet.
Soutěž probíhá online, nemusíte se svým týmem sejít na jednom místě. Týmy ale musí pocházet z jedné školy.
Tak na co čekáš, registruj se na Mathrace!
Již tradiční internetová soutěž Mathrace (http://brkos.math.muni.cz/mathrace/)
proběhne už za týden v úterý 30.11.! Soutěž je určena pro nejvýše čtyřčlenné týmy středoškoláků, pro nadšence mimo střední školu je tu kategorie Underground. Soutěž organizují studenti Přf MUNI.
Čím se liší Mathrace od jiných matematických soutěží? Na řešení úloh jsou povolené libovolné zdroje - kalkulačky, Geogebra, WolframAlpha, programování - můžete si proto být jistí, že i s pomocí těchto nástrojů budete muset nad úlohami přemýšlet.
Soutěž probíhá online, nemusíte se svým týmem sejít na jednom místě. Týmy ale musí pocházet z jedné školy.
Tak na co čekáš, registruj se na Mathrace!
Áďa | org | 15. 11. 2022 12:46:01
Ahoj! Druhá podzimní série je za námi. Pokud si s nějakým příkladem marně lámeš hlavu, níže si můžeš prohlédnout hinty, které Ti pomůžou vydat se správným směrem.
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text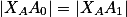 + skrytý text
+ skrytý text
Úloha 1.+ skrytý text
Popáruj si vzdálenosti, aby se sečetly na 9
Úloha 2.+ skrytý text
Dokresli čtverec, jehož úhlopříčka je 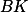 .
.
Úloha 3.+ skrytý text
Parita (sudost/lichost)
Úloha 4.+ skrytý text
Ukaž, že chatrč může být kdekoli mezi 1011. a 1012. hruškou.
Úloha 5.+ skrytý text
Dokresli si průsečíky úhlopříček zadaných obdélníků. Pomocí nich dokaž, že 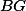 je rovnoběžná s
je rovnoběžná s 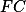 .
.
Úloha 6.+ skrytý text
Buďte 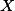 ,
, 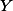 středy
středy 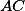 ,
, 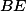 ; potom ukaž, že
; potom ukaž, že 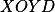 je rovnoběžník.
je rovnoběžník.
Úloha 7.+ skrytý text
Dokažte tětivovost 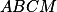 a
a 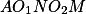
Úloha 8.+ skrytý text
Chordála Feuerbachovy kružnice a kružnice opsané
Michal Janík | org | 19. 7. 2022 22:29:35
Řešení 15:
+ skrytý text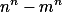 můžeme zapsat jako
můžeme zapsat jako 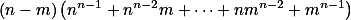 . Teď dokážeme, že tyto dvě závorky jsou nesoudělné. Skutečně
. Teď dokážeme, že tyto dvě závorky jsou nesoudělné. Skutečně 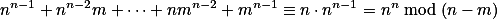 . Proto
. Proto 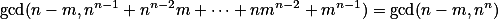 (Eukleidův algoritmus). Pokud by ale nějaké prvočíslo dělilo jak
(Eukleidův algoritmus). Pokud by ale nějaké prvočíslo dělilo jak 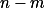 , tak
, tak 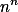 , pak by dělilo i
, pak by dělilo i  a
a 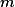 , což je spor s jejich nesoudělností. Tudíž jsou závorky vskutku nesoudělné. Jelikož jejich součin je čtverec, i obě závorky jsou čtverce, tedy skutečně je
, což je spor s jejich nesoudělností. Tudíž jsou závorky vskutku nesoudělné. Jelikož jejich součin je čtverec, i obě závorky jsou čtverce, tedy skutečně je 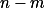 čtverec.
čtverec.
Zadání 16:
V rovině leží několik přímek tak, že každá přímka protíná přesně jiných přímek. V závislosti na
jiných přímek. V závislosti na  určete, kolik přímek může v rovině ležet.
určete, kolik přímek může v rovině ležet.
+ skrytý text
Zadání 16:
V rovině leží několik přímek tak, že každá přímka protíná přesně
Erik Ježek | 27. 5. 2022 20:04:00
Řešení 14:
+ skrytý text
Zadání 15:
Mějme přirozená čísla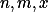 , taková že splňují
, taková že splňují 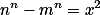 a čísla
a čísla 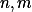 jsou nesoudělná. Dokažte že
jsou nesoudělná. Dokažte že 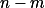 je druhou mocninou přirozeného čísla
je druhou mocninou přirozeného čísla
+ skrytý text
Když za 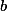 budeme dosazovat čísla od 0 do
budeme dosazovat čísla od 0 do 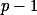 , tak dostaneme
, tak dostaneme  různých zbytků modulo
různých zbytků modulo  , protože: Pro spor předpokládejme, že existují různá celá čísla
, protože: Pro spor předpokládejme, že existují různá celá čísla 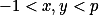 , taková že
, taková že 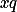 a
a 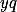 dávají stejný zbytek, pak ale musí platit, že
dávají stejný zbytek, pak ale musí platit, že  dělí
dělí 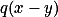 a z toho že
a z toho že  a
a 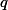 jsou různá prvočísla, tak
jsou různá prvočísla, tak  dělí
dělí 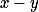 , to ale už znamená
, to ale už znamená 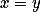 , což je spor. Zbývá ukázat, že každý z těchto zbytků je menší než
, což je spor. Zbývá ukázat, že každý z těchto zbytků je menší než 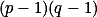 , nebo je prvním větším číslem než tento součin, které dává stejný zbytek modulo
, nebo je prvním větším číslem než tento součin, které dává stejný zbytek modulo  jako
jako 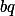 (proto je v následující nerovnosti na levé straně
(proto je v následující nerovnosti na levé straně 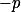 ), pak bude jistě stačit zvolit
), pak bude jistě stačit zvolit  nezáporně pro každé
nezáporně pro každé 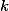 . Podmínku stačí ověřit pro nejvyšší
. Podmínku stačí ověřit pro nejvyšší 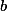 , tedy pro
, tedy pro 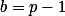 , pak chceme dokázat:
, pak chceme dokázat: 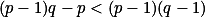 , což ale triviálně platí a tím jsme hotovi
, což ale triviálně platí a tím jsme hotovi
Zadání 15:
Mějme přirozená čísla
Patrik Štencel | org | 22. 5. 2022 23:33:25
Řešení 13:
+ skrytý text
Zadání 14:
Mějme dvě prvočísla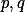 . Dokažme, že pro každé
. Dokažme, že pro každé 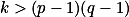 lze
lze 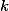 zapsat jako
zapsat jako 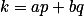 pro nezáporná celá čísla
pro nezáporná celá čísla  .
.
+ skrytý text
Rozdělme si políčka na rohová, okrajová(nepatří do nich rohová) a vnitřní. Rohová mají pouze 2 sousedy, takže nemůže být obarvené. Okrajové má 3 sousedy, takže všichni 3 musí být obarveni. Tabulka je konečná, takže se dostaneme k rohovému políčku, které nemůže být obarvené a tedy ani okrajové nemůže být. Nyní se podívejme na vnitřní políčka. Představme si, že tvoří nějaký mnohoúhelník, kde jeho úhly jsou násobky 90°. Představme si, že nějaký vnitřní úhel má 90°. To by znamenalo, že nějaké políčko má kolem sebe 2 čtverečky. To odporuje zadání, takže jeho jediné vnitřní úhly jsou 180°, 270°,360°(uvnitř). Pokud bychom šli po jeho vnějším obvodu(nepočítáme vnitřní záhyby), mohli bychom sečíst úhly na které narazíme. Pokud bychom brali ty úhly, které nejsou přímé a náš mnohoúhelník by měl n vrcholů, získali bychom tento součet jako n270°. Součet úhlů v mnohoúhelníku je (n-2)180°. Tedy náš útvar nemůže být mnohoúhelník, ale zároveň jediný útvar, který by to mohl být je mnohoúhelník. To je spor a tedy nejde to. (Alternativní metoda by spočívala, že půjdeme po obvodu a vždy budeme zabočovat o 90° na jednu stranu a na druhé straně se bude rozkládat náš obarvený mnohoúhelník. Nyní bychom potřebovali obalit náš mnohoúhelník tím, že uzavřeme jeho obvod. Problém by nastal v tom, že u každého takového uzavření by obarvená část nebyla uvnitř uzavřené části, ale venku(táhla by se do nekonečna/krajů(obojí nejde)).)
Zadání 14:
Mějme dvě prvočísla
Erik Ježek | 22. 5. 2022 20:24:20
Řešení 12:
+ skrytý text
Zadání 13:
Uvažme tabulku s řádky a
řádky a 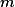 sloupci. Lze tuto tabulku obarvit, tak aby každé obarvené políčko (existuje aspoň jedno) sousedilo s aspoň 3 jinými obarvenými políčky? (Políčko sousedí s jiným políčkem, pokud mají společnou stranu)
sloupci. Lze tuto tabulku obarvit, tak aby každé obarvené políčko (existuje aspoň jedno) sousedilo s aspoň 3 jinými obarvenými políčky? (Políčko sousedí s jiným políčkem, pokud mají společnou stranu)
+ skrytý text
Stačí zvolit 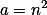 ,
, 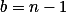 , pak rovnost jistě bude platit a jmenovatel zlomku bude vždy vyšší než 0 (z přirozenosti
, pak rovnost jistě bude platit a jmenovatel zlomku bude vždy vyšší než 0 (z přirozenosti  ).
).
Zadání 13:
Uvažme tabulku s
Matěj Doležálek | org | 15. 5. 2022 01:05:18
Řešení 11:
+ skrytý text
Zadání 12:
Je dáno přirozené číslo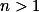 . Dokaž, že lze zvolit přirozená
. Dokaž, že lze zvolit přirozená  ,
, 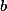 tak, že
tak, že 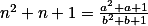 .
.
+ skrytý text
Pojmenujme středy 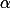 ,
, 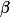 ,
, 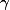 jako
jako 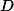 ,
, 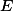 ,
, 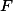 a jejich společný bod označme
a jejich společný bod označme 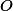 . Obě
. Obě 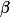 ,
, 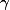 jsou osově souměrné podle
jsou osově souměrné podle 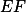 , takže jejich druhý průsečík musí být obrazem
, takže jejich druhý průsečík musí být obrazem 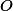 podle téhle osy -- můžeme tedy
podle téhle osy -- můžeme tedy  alternativně pojmenovat jako
alternativně pojmenovat jako 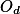 . Obdobně mějme
. Obdobně mějme 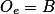 ,
, 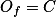 . Zjevně je
. Zjevně je 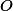 opsiště trojúhelníku
opsiště trojúhelníku 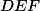 , ukažme, že opsištěm
, ukažme, že opsištěm 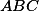 je kolmiště
je kolmiště 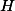 trojúhelníku
trojúhelníku 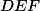 . Označíme-li jeho obrazy v osových souměrnostech podle stran
. Označíme-li jeho obrazy v osových souměrnostech podle stran 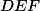 jako
jako 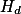 ,
, 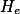 ,
, 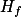 , pak máme
, pak máme 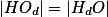 , což je jen poloměr opsané kružnice
, což je jen poloměr opsané kružnice 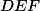 , protože
, protože 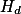 leží na kružnici opsané (to je známé). Tím je dokázáno, že
leží na kružnici opsané (to je známé). Tím je dokázáno, že 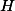 je středem kružnice opsané
je středem kružnice opsané 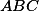 a její poloměr je
a její poloměr je 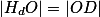 , což je původní poloměr našich kružnic.
, což je původní poloměr našich kružnic.
Zadání 12:
Je dáno přirozené číslo
Michal Janík | org | 14. 5. 2022 12:21:45
11:
Kružnice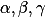 se stejným poloměrem se protínají v jednom bodě. Jejich další průsečíky jsou
se stejným poloměrem se protínají v jednom bodě. Jejich další průsečíky jsou 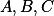 . Dokažte, že kružnice opsaná
. Dokažte, že kružnice opsaná 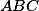 má stejný poloměr.
má stejný poloměr.
Kružnice
Michal Janík | org | 14. 5. 2022 12:18:36
Když už skončil myšmaš, mohli bychom zkusit obnovit maraton, ne? : D
Řešení 10:
+ skrytý text
Řešení 10:
+ skrytý text
Je známé, že 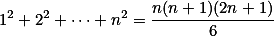 , nerovnost ze zadání můžeme upravit na
, nerovnost ze zadání můžeme upravit na 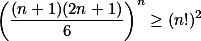 . Navíc
. Navíc ![\frac{(n+1)(2n+1)}6=\frac{n(n+1)(2n+1)}{6n}=\frac{1^2+2^2+\cdots+n^2}n\geq \sqrt[n]{1^2\cdot2^2\cdots n^2} \frac{(n+1)(2n+1)}6=\frac{n(n+1)(2n+1)}{6n}=\frac{1^2+2^2+\cdots+n^2}n\geq \sqrt[n]{1^2\cdot2^2\cdots n^2}](https://prase.cz/chat/texmaker.php?tex=%5Cfrac%7B%28n%2B1%29%282n%2B1%29%7D6%3D%5Cfrac%7Bn%28n%2B1%29%282n%2B1%29%7D%7B6n%7D%3D%5Cfrac%7B1%5E2%2B2%5E2%2B%5Ccdots%2Bn%5E2%7Dn%5Cgeq+%5Csqrt%5Bn%5D%7B1%5E2%5Ccdot2%5E2%5Ccdots+n%5E2%7D&hash=dc87371c0e1355e2e8a3) . Umocněním na
. Umocněním na  -tou dostáváme přesně to, co jsme chtěli.
-tou dostáváme přesně to, co jsme chtěli.
Kateřina Panešová | 7. 4. 2022 10:40:15
Ahoj! Jistě se už nemůžeš dočkat dvojité várky hintů, a to ke 3. jarní a 3. seriálové sérii!
Úloha 1. + skrytý text
Úloha 2. + skrytý text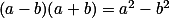
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8.+ skrytý text
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
+ skrytý text
Úloha 1. + skrytý text
Použij mocniny dvojky.
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Modulo 4.
Úloha 4. + skrytý text
Mocni a zbavuj se racionálních čísel.
Úloha 5. + skrytý text
Označ 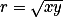 ,
, 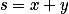 a vyjádři v
a vyjádři v  a
a  rovnice ze zadání.
rovnice ze zadání.
Úloha 6. + skrytý text
Dokresli PA a PB a hledej podobné trojúhelníky.
Úloha 7. + skrytý text
Podívej se na cestu délky L a délku cyklu, na němž leží první a poslední vrchol, označ jako K. Ukaž, že existuje cyklus délky alespoň 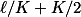 .
.
Úloha 8.+ skrytý text
Levou stranu zdola odhadni jako 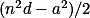 , kde a = dolní celá část z
, kde a = dolní celá část z 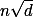 .+ skrytý text
.+ skrytý text
Vyluč malé hodnoty 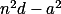 pomocí kvadratických zbytků pro vhodnou zbytkovou třídu d mod 20.
pomocí kvadratických zbytků pro vhodnou zbytkovou třídu d mod 20.
Úloha 1. + skrytý text
Rozepiš Eukleidův algoritmus pro 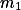 a
a 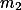 a všechny rovnosti vynásob
a všechny rovnosti vynásob  .
.
Úloha 2. + skrytý text
Použij Eukleidův algoritmus a všimni si, že Eukleidův algoritmus platí i u exponentů.
Úloha 3. + skrytý text
Všimni si, že součet a+b se zachovává a zároveň jsou obě čísla nezáporná. + skrytý text
Proto to nemůže skončit jinak, než že první číslo je nula a druhé je 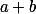 .
.
+ skrytý text
Pokud se (a,b) změní na (c,d), tak NSD(c,d) dělí 2*NSD(a,b).+ skrytý text
Na konci tedy musí platit a+b dělí NSD(a,b)*2^k.
Áďa | org | 8. 3. 2022 09:20:28
Vrtá Ti stále hlavou nějaký příklad ze 2. jarní série? Nevěš ramena a prohlédni si hinty:
Úloha 1. + skrytý text
Úloha 2. + skrytý text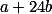 musí být násobkem
musí být násobkem 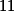 i
i 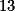 .
.
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Zkus za většinu hledaných čísel zvolit jedničku.
Úloha 2. + skrytý text
Úloha 3. + skrytý text
V zápisu čísla zkus použít co nejvíc devítek.
Úloha 4. + skrytý text
Všimni si, že body  ,
, 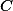 ,
, 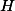 a
a 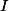 leží na kružnici.
leží na kružnici.
Úloha 5. + skrytý text
Dokresli střed jedné úhlopříčky a uvaž střední příčky, které tím vzniknou.
Úloha 6. + skrytý text
Dvakrát si rozepiš rekurenci a potom rozlož na součin.
Úloha 7. + skrytý text
Nahlédni, že 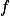 musí být 3-periodická.+ skrytý text
musí být 3-periodická.+ skrytý text
Vyjádři dvěma způsoby 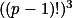 .
.
Úloha 8. + skrytý text
Vyřeš zvlášť případ, kdy jedno z prvočísel je 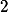 .+ skrytý text
.+ skrytý text
Pokud jsou obě prvočísla lichá, najdi spor pomocí 2-valuace rozdílu 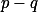 a řádů dvojky modulo
a řádů dvojky modulo 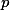 a
a 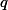 .
.
Áďa | org | 9. 2. 2022 11:38:55
Ahoj! Nepochybně i Ty netrpělivě vyhlížíš hinty k 1. jarní a 2. seriálové sérii. Zde jsou:
1j
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
2s
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
1j
Úloha 1. + skrytý text
Zkus párovat vybarvené a nevybarvené trojúhelníčky.
Úloha 2. + skrytý text
Chytře vyjádři 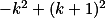 .
.
Úloha 3. + skrytý text
Spočítej počet průsečíků.
Úloha 4. + skrytý text
Podívej se, kde může být n a n-1. Dokaž rekurenci.
Úloha 5. + skrytý text
Podívej se na rozdíl osamělosti sousedů.
Úloha 6. + skrytý text
Seřaď stromy podle výšky.
Úloha 7. + skrytý text
Přičti ke všem rovnicím 1. Nově získané rovnice vynásob. Použij AG nerovnost.
Úloha 8. + skrytý text
Uprav na 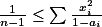 .+ skrytý text
.+ skrytý text
Použij Cauchy-Schwarzovu nerovnost.
2s
Úloha 1. + skrytý text
Použij indukci na  .+ skrytý text
.+ skrytý text
V základním kroku ukaž, že rovnost platí pro 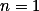 a všechna
a všechna 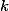 neboli
neboli 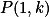 , v indukčním kroku ukaž implikaci
, v indukčním kroku ukaž implikaci 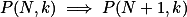 pro všechna
pro všechna 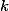 .
.
Úloha 2. + skrytý text
Pro první, druhý i třetí vztah použij indukci podle  . Nezapomeň zmínit, kde používáš vlastnosti již dříve dokázané v seriálu (např. komutativita násobení).
. Nezapomeň zmínit, kde používáš vlastnosti již dříve dokázané v seriálu (např. komutativita násobení).
Úloha 3. + skrytý text
Přenásob 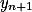 číslem
číslem 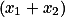 a použij Vietovy vztahy.
a použij Vietovy vztahy.
Áďa | org | 12. 1. 2022 20:06:27
Lámeš si stále hlavu nad některými úložkami ze 4. podzimní série? Nová várka hintů Ti spěchá na pomoc.
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text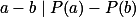
Úloha 4. + skrytý text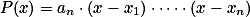
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text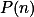 nemůže mít velkého dělitele menšího než
nemůže mít velkého dělitele menšího než  .+ skrytý text
.+ skrytý text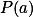 bude nutně dělit i nějaké další
bude nutně dělit i nějaké další 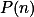 .
.
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Součet stupňů je menší než stupeň součtu.
Úloha 2. + skrytý text
Rozlož polynom na součin.
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Ze zadaného vztahu zjisti součet 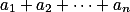 . + skrytý text
. + skrytý text
Pro 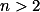 zjisti součet
zjisti součet 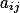 pro všechna
pro všechna 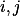 , případ
, případ 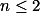 rozeber zvlášť.
rozeber zvlášť.
Úloha 6. + skrytý text
Podívej se na stupně polynomů. Ukaž, že P má kořen v 0.
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Na lichých mocninách nezáleží.+ skrytý text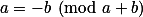 + skrytý text
+ skrytý text
Pokud máš víc než jeden člen se sudou mocninou, vyděl vhodnou mocninou 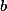 a polož rovnost.
a polož rovnost.
Kateřina Panešová | 8. 12. 2021 18:49:36
Zdravím všechny příznivce hintů 3. podzimní a 1. seriálové série!
3p
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6.+ skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
1s
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
3p
Úloha 1. + skrytý text
Vytvořte dlouhý rovnoběžník a poté na něj postupně přidávejte zuby.
Úloha 2. + skrytý text
Vyberte průměr, a poté libovolný ze zbylých vrcholů. Vyřeště kvadratickou rovnici.
Úloha 3. + skrytý text
1,4,5,2,3,6
Úloha 4. + skrytý text
Dokresli úsečku 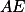 a vyčísli úhly. + skrytý text
a vyčísli úhly. + skrytý text
Ukaž, že trojúhelník 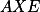 je rovnoramenný.
je rovnoramenný.
Úloha 5. + skrytý text
Uvažujte cykly vzniklé přeskakováním vždy o 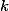 vrcholů doprava. Všimněte si, že rozdíl počtu dvojic červených vrcholů po sobě a modrých vrcholů po sobě je roven rozdílu počtu červených a modrých vrcholů v cyklu.
vrcholů doprava. Všimněte si, že rozdíl počtu dvojic červených vrcholů po sobě a modrých vrcholů po sobě je roven rozdílu počtu červených a modrých vrcholů v cyklu.
Úloha 6.+ skrytý text
Ukažte, že kružnice se středem v A a poloměrem 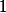 se dotýká úsečky
se dotýká úsečky 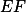 . (Např. pomocí překlopení bodu
. (Např. pomocí překlopení bodu  podél
podél 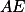 a
a 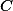 podél
podél 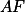 .)
.)
Úloha 7. + skrytý text
Podívejte se na středové úhly jednotlivých tětiv kružnice. Musí být po dvou různé a dva vedlejší musí mít vždy celočíselný průměr.+ skrytý text
Pro 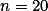 lze udělat konstrukce, pro
lze udělat konstrukce, pro 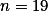 musíme volit celočíselné velikosti jednotlivých úhlů a do plného úhlu
musíme volit celočíselné velikosti jednotlivých úhlů a do plného úhlu 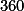 se nemůžou vejít.
se nemůžou vejít.
Úloha 8. + skrytý text
Uvažujte cestičky vytvořené paralelním přesouváním úseček délky jedna podél dlaždiček libovolného dláždění. + skrytý text
Každé dvě cestičky, které nemají stejně orientované úsečky, se protínají právě na jednom místě a jednoznačně určují typ dlaždičky. Počet cestiček různých typů nezávisí na vydláždění.
1s
Úloha 1. + skrytý text
Indukce na n=počet prvků S.
Úloha 2. + skrytý text
Silná indukce pro n větší než 10, které zapiš jako 10a+b.
Úloha 3. + skrytý text
Ukaž, že pro sudý počet palačinek otočených spálenou stranou vyhrát nemůže, a naopak zkonstruuj strategii, podle které vyhraje, pokud je palačinek otočených spálenou stranou nahoru lichý počet. Silná indukce.
Kateřina Panešová | 7. 10. 2021 09:56:12
Ahoj! Jistě již netrpělivě očekáváte hinty k 1. podzimní sérii! Pro nové řešitele: Po termínu odeslání zveřejňujeme malé nápovědy k soutěžním úlohám, takže si můžete zkusit vyřešit i úlohy, u kterých jste si nevěděli rady :)
Umění
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Umění
Úloha 1. + skrytý text
Opačná úhlopříčka
Úloha 2. + skrytý text
Slož dvě osové souměrnosti.
Úloha 3. + skrytý text
Nejbližší dva body
Úloha 4. + skrytý text
Vietovy vztahy a mocnost
Úloha 5. + skrytý text
8 a 7 nefungují; 5 a 6 nelze použít zároveň
Úloha 6. + skrytý text
Přesubstituuj do částečných součtů.
Úloha 7. + skrytý text
Dokresli středy 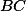 a
a 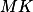 .
.
Úloha 8. + skrytý text
Dokresli přes trojúhelníky větší útvary, které se stále nebudou překrývat. + skrytý text
Rozšiř na šestiúhelník tak, aby se ani žádné dva šestiúhelníky nepřekrývaly.
Dominik Stejskal | 13. 5. 2021 03:36:46
Než dojde další ročník ke svému konci, je tu ještě jedna várka hintů ke 4. jarní sérii. :)
Úloha 1.
(a) + skrytý text
(b) + skrytý text
Úloha 2.
(a) + skrytý text
(b) + skrytý text
Úloha 3.
(a) + skrytý text
(b) + skrytý text
Úloha 4.
(a) + skrytý text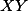 prochází středem čtverce.
prochází středem čtverce.
(b) + skrytý text
Úloha 5.
(a) + skrytý text
Úloha 6.
(a) + skrytý text
(b) + skrytý text
Úloha 7.
(a) + skrytý text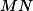 je těžnice v
je těžnice v 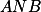 i
i 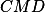 .
.
(b) + skrytý text
Úloha 1.
(a) + skrytý text
Ukaž, že body 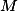 ,
, 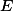 ,
, 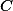 a
a 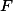 leží na jedné kružnici.
leží na jedné kružnici.
(b) + skrytý text
Překlop body  a
a 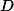 po řadě podle úseček
po řadě podle úseček 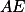 a
a 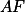 a označ obrazy
a označ obrazy 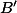 ,
, 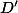 . Ukaž, že
. Ukaž, že  ,
, 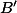 ,
, 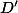 leží na přímce a
leží na přímce a 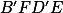 je rovnoběžník. + skrytý text
je rovnoběžník. + skrytý text
V rovnoběžníku se půlí úhlopříčky. Následně hledej shodné trojúhelníky.
Úloha 2.
(a) + skrytý text
V pravoúhlém trojúhelníku je poloměr kružnice vepsané = (odvěsna + odvěsna - přepona) / 2.
(b) + skrytý text
Rozděl vyhovující permutace na skupinky po 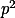 . + skrytý text
. + skrytý text
Pokud 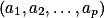 vyhovuje, pak vyhovují i permutace tvaru
vyhovuje, pak vyhovují i permutace tvaru 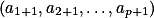 a
a 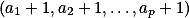 , kde
, kde 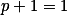 . + skrytý text
. + skrytý text
Rozmysli si, že opakovanou aplikací tohoto algoritmu lze dostat přesně permutace tvaru 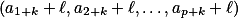 , kde
, kde 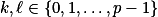 a všechny indexy a hodnoty bereme modulo
a všechny indexy a hodnoty bereme modulo 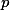 mezi
mezi 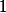 a
a 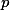 . Takto vyrobíme spoustu disjunktních skupinek vyhovujících permutací, které jsou velké nejvýše
. Takto vyrobíme spoustu disjunktních skupinek vyhovujících permutací, které jsou velké nejvýše 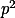 . Které z nich jsou menší než
. Které z nich jsou menší než 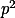 ? + skrytý text
? + skrytý text
Ukaž, že to jsou přesně permutace s konstantní diferencí 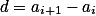 pro všechna
pro všechna 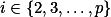 .
.
Úloha 3.
(a) + skrytý text
Podívej se na cestu mezi políčky s čísly 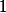 a
a 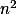 .
.
(b) + skrytý text
Kolik je kostiček potřeba k tomu, aby se už další nedala přiložit do jednoho čtverce 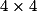 ?
?
Úloha 4.
(a) + skrytý text
(b) + skrytý text
Uvažme nejmenší kruh obsahující všechny body. Můžou všechny body na okraji být součástí jedné půlkružnice?
Úloha 5.
(a) + skrytý text
V některou hodinu budou u trezoru 3 orgové. + skrytý text
Jednoho z nich lze propustit.
Úloha 6.
(a) + skrytý text
Velká prvočísla by bylo potřeba spárovat s jedničkou. + skrytý text
Jde zařídit 12 celočíselných zlomků.
(b) + skrytý text
Jde to pro všechna  . Konstruuj
. Konstruuj  -tici induktivně. + skrytý text
-tici induktivně. + skrytý text
Přidej nulu a ke všemu přičti vhodné číslo.
Úloha 7.
(a) + skrytý text
(b) + skrytý text
Chceš dokázat 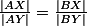 . + skrytý text
. + skrytý text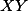 a společné tečny z bodů
a společné tečny z bodů  ,
,  se protínají v jediném bodě
se protínají v jediném bodě 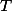 .
.




