Chat Prasátek

Matematická sekce

Marián Poppr | 15. 12. 2015 19:02:32

Ano, jsou tu vždy po uzávěrce a před hotovými vzoráky, aby si každý mohl buď skusit dořešit úlohy, s kterými třeba válčil. A nebo když je nedočkavý, tak pomocí hintů nahlédl, že měl odeslané řešení správné.

Marco Souza de Joode | 14. 12. 2015 22:03:09

Hele, vy zveřejňujete ty nápovědy až po uzávěrce?

Marián Poppr | 14. 12. 2015 21:09:14

Ahoj!

Na povrch vyplavaly a světlo světa spatřily NÁPOVĚDY k nejen 3. sérii, ale dokonce i 1. seriálové serii..

3.série

Úloha 1+ skrytý text

Jde to...

Úloha 2+ skrytý text

Nejde to...+ skrytý text

Jak by vypadal graf, kde vrcholy reprezentují políčka šachovnice a hrany odpovídají skokům koně mezi políčky?

Úloha 3+ skrytý text

Jde to...+ skrytý text

Neklesat na mysli a chvilku si hrát :)

Úloha 4+ skrytý text

Lze to pro všechny čtverce o straně 4n-2 + skrytý text

Pro konstrukci tohoto případu skus např. z T tetronim složit čtverec 4*4 a ten obalit čtverci 2*2+ skrytý text

Snadno lze nahlédnout, že čtverce o liché straně nejdou poskládat+ skrytý text

Zbývající případ 4n skus vyvrátit obarvením šachovnice a zkoumej kolik je potřeba nahradit čtverců za t-tetronima, a jak se ti při tom mění parita barev na šachovnici.

Úloha 5+ skrytý text

Bára má vyhrávající strategii+ skrytý text

Co kdyby se jí podařilo vytvořit si nějaké volné políčko pro L u rohu, které nelze ani z části překrýt čtvercem?

Úloha 6+ skrytý text

Jak se změní aritmetický průměr všech políček po Mínusíkově nebo Plusíkově tahu? A jak se změní hodnota prostředního políčka?+ skrytý text

Jelikož na konci se průměr bude rovnat prostřednímu políčku, tak zkuste zjistit, jakou hodnotu mělo na začátku?+ skrytý text

Zbývá ukázat, že konečná hodnota všech políček může být pouze 5

Úloha 7+ skrytý text

Skuste úlohu vyřešit sporema.+ skrytý text

Tedy věže by se na řádcích a sloupcích pouze zpermutovali, jaká by pak byla hodnota výrazu, když bychom sečetly všechny absolutní hodnoty rozdílů Pi-i a qi-i (kde Pi a qi jsou permutace na řádcích a sloupcích pro odpovídající políčko na šachovnici) + skrytý text

Dostaneme liché číslo 3*2015+ skrytý text

Ukažte však, že každá suma (přes řádky a sloupce) má hodnotu sudého čísla

Úloha 8 + skrytý text

Úloha má řešení jen pro šachovnice o rozměrech stran, které jsou mocninou dvojky+ skrytý text

Kolik je možností jak zakódovat šachovnici?+ skrytý text

Pak by musel Štěpán otočením jednoho políčka získat n^2 zakódovaných stavů, co z toho pak pro rozměry šachovnice? + skrytý text

Zbývá najít pro n mocninu dvojky strategii Štěpána a Davida. Označ si políčka 0 až n^2-1 a zkoumej jejich binární zápis.+ skrytý text

David si zvolí políčko s hodnotou XOR všech políček třeba s bílou barvou. Když Štěpán dostane stav s hodnotou XORu bílých políček a ,a Rado si vybere políčko b, tak zbývá ukázat, že stačí změnit knoflík na políčku aXORb.

Seriál

Úloha 1 + skrytý text

Skus vyplňovat číselnou od nějakého bodu na obě dvě strany, tak aby si v nějakém kroku určitě pastmi přeskočil blechu a zároveň jí stihl uzavřít.+ skrytý text

Zvol si nějakou dostatečně rychle rostoucí funkci

Úloha 2 + skrytý text

Najdi prosté zobrazení z P(R+) do X + skrytý text

Skus si vzít zobrazení takové, které by každé podmonožině M z R+ přiřadilo bijekci, jež pro všechny kladná a přiřadila identitu nebo zapornoua, podle toho jestli jsou v M nebo ne.

Úloha 3 + skrytý text

Mějme rekurzivně w^n=w*w^(n-1) , je w^n DUMa?+ skrytý text

Porovnáváme lexikograficky zprava

+ skrytý text

Položme potom w^w jakožto, posloupnost přirozených čísel s jen konečným počtem nenulových čísel a opět ukažme, že jde o DUMu+ skrytý text

Stačí tedy najít rostoucí bijekci :)+ skrytý text

Vezměme si zobrazení (n,ai) na (bi) pro i jdoucí do nekonečna a zároveň b1=n a bx=ax-1 pro x>1, ukaž že je bijekcí a poté trochu zatněme zuby a dopočítejme, že je toto zobrazení opravdu rostoucí

Marián Poppr | 15. 11. 2015 15:30:32

Ahoj,
slyšte tu užasnou a skvělou, jedinečnou a neopakovatelnou novinu, jsou tady NÁPOVĚDY k 2. sérii!! Tak neváhejte a využijte tuto fantastickou příležitost.

Úloha 1+ skrytý text

Ukažte, že takový organizátor nemusí existovat.

Úloha 2+ skrytý text

165 vyhraných zápasů už je moc..

Úloha 3+ skrytý text

Označme bodem F střed BC a bodem H průsečík přímek AF a BD, co víme o trojúhelnících AHB a FHD?+ skrytý text

V jakém jsou poměru?

Úloha 4+ skrytý text

Jaké jsou trojúhelníky AM1M2 a AN1N2 nebo AM2M3 s AN2N3?+ skrytý text

Skus to zjistit přes obvodové úhly.

Úloha 5+ skrytý text

Jaký je trojúhelník KLP? A co se dá říct o bodu M ve vztahu k tomuto trojúhelníku?+ skrytý text

Ukaž, že Q je těžiště trojúhelníku KPN.

Úloha 6+ skrytý text

Ukaž, že pro libovolná 4 x,y,z,w čísla z vykutálené množiny platí, že xy-zw je racionální.+ skrytý text

Nepomohlo by nám náhodou, kdyby i x(y-z) bylo racionální?

Úloha 7+ skrytý text

Ukaž, že trojúhelníky ABK a CAK jsou podobné, co z toho pak plyne pro strany AK,BK,CK?+ skrytý text

Použijte kosinovou větu pro trojúhelníky ABC, AKC, ABK, BCK a ACE (kde E je obraz bodu A ve středové souměrnosti podle M). Pak zatněte zuby a dopočítejte se výsledku :)

Úloha 8+ skrytý text

Pro začátek si rozmysli několik vlastností ciferných součtů: (1) pokud číslo vynásobíme 10, tak se jeho cif. součet nezmění. (2) S(a+b)<=S(a)+S(b). (3) S(ab)<=S(a)S(b) (použij tvrzení (1) a (2))+ skrytý text

No a teď se můžeme vrhnout zpátky na úlohu, zbývá ukázat, že S(n)/S(16n)<=S(625)

Ondra | 20. 10. 2015 20:42:03

Jestli to má řešení nevím, já se spíš pokouším dokázat, že žádné neexistuje. Původní myšlenka byla sevřít to mezi dvě po sobě jdoucí druhé mocniny, ale to se bohužel nepovedlo. Ještě mě napadlo $\textstyle a!$ vyjádřit pomocí dostatečně 'jemného' Stirlinga (označme tu aproximaci jako $\textstyle f(a)$ ) a pak nějakou ošklivou indukcí zkusit dokázat nerovnosti $\textstyle a^a+a!<a^a+f(a)<\left(\left\lfloor\sqrt{a^a+a!-1}\right\rfloor+1\right)^2$ , ale do toho se mi zatím moc nechce...

Miroslav Olšák | org | 20. 10. 2015 13:42:30

Přinejensím, když $a$ je prvočíslo, tak nevyjde $a$ -valuace, tedy to v takovém případě nemá řešení. Jinak nevím.

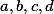Ví se, že to má nějaké rozumný důkaz? Podobné diofantické rovnice jsou leckdy otevřený problém. Hodně známá je velká Fermatova věta (řešte $a^n+b^n=c^n$ pro $a,b,c,d$ přirozená a $n>2$ ), která byla dokázána nedávno a dost složitě.

Pokud vím, tak například je dosud otevřený problém, zdali má rovnice $n!+1=a^2$ víc než tři celočíselná řešení (a to ta tři řešení jsou do první desítky).

Ondra | 19. 10. 2015 23:15:27

Já se dostal pouze k tomuto
$\textstyle \left\lfloor\sqrt{a^a+a!-1}\right\rfloor^2<a^a+a!=\left(\sqrt{a^a+a!-1}-1\right)^2+2\sqrt{a^a+a!-1}<\left\lfloor\sqrt{a^a+a!-1}\right\rfloor^2+$ $\textstyle +2\sqrt{a^a+a!-1}<\left\lfloor\sqrt{a^a+a!-1}\right\rfloor^2+2\left(\left\lfloor\sqrt{a^a+a!-1}\right\rfloor+1\right)=$ $\textstyle =\left(\left\lfloor\sqrt{a^a+a!-1}\right\rfloor+1\right)^2+1$

Z toho ihned plyne, že pokud má rovnice řešení, pak nutně $\textstyle b=\left\lfloor\sqrt{a^a+a!-1}\right\rfloor+1$ , ale nic zajímavého se mi z toho vyzřískat nepodařilo...

Marek Pospíšil | 19. 10. 2015 19:58:14

Můj prvotní nápad byl rozložit levou stranu, neboť a! lze zapsat jako ((a umocněno na a) mínus něco), ale vyjádřit to něco může být docela fuška:-)Pak snad s tím tvarem dokážeš, že to nejde(což si osobně myslím...nebo si uhádnul nějaké řešení???). Čistě matematický postup bude asi dost komplikovaný a těžký, osobně bych to nějak doslepil úvahou...
Á propos: může se ti u toho hodit vědět, že 1+2+3+4+5=(5+5 na druhou)/2, což by mělo analogicky platit v rámci všech přirozených čísel.

Ondra | 16. 10. 2015 23:18:18

Ahojte, nevěděl by někdo, jak jít na rovnici $a^a+a!=b^2,a,b\in\mathbb N$ ? Na českém matfóru už leží pár měsíců bez odezvy a mi to přijde škoda. (:

Marián Poppr | 12. 10. 2015 23:59:26

Ahoj,
jsou tady nápovědy k první serii

úloha 1+ skrytý text

Dokáže Pepa na jednu otázku poznat, zda-li se ve dvojici PraSátek nachází vlk?

úloha 2+ skrytý text

Ano, může se mu to podařit. Podívejte se, pro jaké kružnice vyhovuje množina modrých bodů tvořící přímku.

úloha 3+ skrytý text

Místo králů prohazujte cesty. Kolik je cest? Může být stejně sypaných cest jako dlážděných?

úloha 4+ skrytý text

Můžeme se nezacyklit (můžeme navštívit patra nad patrem, kam nás pošle první teleport?)?+ skrytý text

Může být cyklus větší než dva? Kam bychom se v něm dostali z nejnižšího patra, na kterém cyklus probíhá, a kam zase toho nejvyššího?

úloha 5+ skrytý text

Pro spor předpokládejte, že žádná z 12 trojic neodbila vícekrát než 20. Ukažte, že nejvíce 20 mohla odbýt pouze každá druhá trojice (zbylé tedy nejvýše 19).+ skrytý text

Sečtěte nerovnosti a ukažte, že platí místo nerovností rovnosti a pak pro spor vhodnou kombinací několika rovnic ukažte, že dvě čarodějem přehozené cifry si jsou rovny.

úloha 6+ skrytý text

Mějme počty čarodějnic v domcích (A1,..,A99) , kde BÚNO A1 je různé od A2, a vezměme si skupinu (A1, A1+A2, A1+A2+A3,.., A1+..+ A99) a rozmyslete si, že v této skupině dává každý člen jiný zbytek po dělení stem + skrytý text

Vezměme si ještě obdobně skupinu (A2, A1+A2, A1+A2+A3,.., A1+..+ A99), no a nyní ukažte, že A1 a A2 dávají stejný zbytek po dělení stem

úloha 7+ skrytý text

Může existovat trpaslík, který krmí doplněk toho druhého? + skrytý text

Pokud existují trpaslíci, co dávají napapat množinám draků A a B, tak existuje i jejich průnik.+ skrytý text

Závěrem ukážeme existenci hledaného trpaslíka, jenž krmí průnik všech ostatních trpaslíků

úloha 8+ skrytý text

Štěpán může vyhrát+ skrytý text

Když odstraníme všechny obarvené vrcholy a hrany z nich vedoucí, tak se strom rozpadne na les. Štěpán se bude snažit udržovat stav, kdy všechny stromy z lesa sousedí maximálně se 2 obarvenými vrcholy. Proč 2?+ skrytý text

Nyní ukaž, že když všechny stromy z lesa sousedí maximálně se 2 obarvenými vrcholy, tak stačí Štěpánovi obarvit vrchol, jenž je v původním stromě spojen hranou nějakým již obarveným vrcholem+ skrytý text

Ukaž, že aby Mirek dokázal utvořit strom se 4 sousedícími obarvenými vrcholy nebo více se 3, tak se mu to musí podařit napoprvé, a pak dokaž, že se mu to nepodaří ani napoprvé

Radovan Švarc | 30. 9. 2015 17:39:18

A přichází dálší série TRiKS! Tato je pravděpodobně spíše těžší než minulá a větší výzva, ale to by vás nemělo odradit od jejího řešení! Naopak se jejím řešením jen více naučíte a více si prohloubíte své dosavadní znalosti. Proto hurá na http://iksko.org/triks/current.php!

David Hruška | org | 14. 9. 2015 22:34:41

A TriKS pokračuje! Od nejbližší půlnoci čtrnáct dní poběží nová soutěž, která je ještě lepší a jednodušší, než byla ta předchozí. Trénujte i Komputační Schopnosti!

Wanderer | 1. 9. 2015 15:49:05

Hezké vysvětlení a pomoc, nicméně já měl na mysli úlohu 8. z 1. podzimní série-"Je není jeden strom...", kdy pro "definici stromu spolu se všemi ostatními potřebnými definicemi" máme jít na mks.mff.cuni.cz/archive/34/uvod1s.pdf

Jinak souhlasím-není potřeba nic zvláštního na vyřešení úloh...

Miroslav Olšák | org | 29. 8. 2015 19:54:35

Ahoj, pro řešení první série není třeba žádná zvláštní teorie, hlavně umět dobře uvažovat a mít dobré nápady ;-) Univerzální textík napříč ročníky a sériemi (spíše pro začátečníky) je: http://mks.mff.cuni.cz/info/Jak.pdf

Někdy (což teď není případ první série) je k sérii ještě stručný doplňující text toho, co pokročilí řešitelé typicky znají, ale ostatním může pomoci. Obecný seznam sérií, textů k nim, případně i vzorových řešení je na stránce aktuálního ročníku ( http://mks.mff.cuni.cz/commentary/commentary.php ). Zatím jsme ale tuto stránku neaktualizovali na současný ročník.

A nakonec (asi to myslel Wanderer) tu bude seriál. Letošní seriál bude na téma "Do nekonečna a ještě dál". Seriál se zaobírá méně známou teorií než běžné série, takže je jeho doprovodný text výrazně delší. Seriál má tři navazující díly -- tři série a tři příslušné doprovodné texty.

Wanderer | 26. 8. 2015 20:15:47

Jediná věc, o níž vím, je sepsaný jakýsi seminář, kterých je tu nejspíš víc, a na který byl odkaz v podzimním zadání...

Sh4rP EYE | 20. 8. 2015 15:27:26

Ahoj, mám jen jednu takovou krátkou otázku. Je tady na stránkách nějaký odkaz na doporučenou teorii (nebo něco podobného), kterou je nutné znát k vyřešení aktualního zadání PraSete? Mám namysli nějaké teorémy, vzorce a podobně.

Vejtek | 3. 8. 2015 00:36:32

Řešení 4. úlohy: + skrytý text

Nakreslíme si grafy funkcí $5-x^2$ a $\sqrt{5-x}$
a všimneme si, že hledáme některá řešení soustavy
$5-y^2 = x \\5-x^2 = y$
Odečteme a upravíme na $(x-y)(x+y-1)=0$ . Nulovost první závorky
vede na kvadratickou rovnici $x^2+x-5=0$ s řešením $x=\frac{-1\pm\sqrt{21}}{2}$ , nulovost druhé závorky vede na rovnici $x^2-x-4$ s kořeny $x=\frac{1\pm\sqrt{17}}{2}$ . Mrknutím na původní obrázek vidíme, že řešením úlohy jsou čísla $\frac{\sqrt{21}-1}{2}$ a $\frac{1-\sqrt{17}}{2}$ .

Úloha 5. + skrytý text

Nalezněte všechny funkce $f\colon\mathbb{R}\setminus\{0\}\to\mathbb{R}$ splňující
$f(x) = x f(1/x)$ a $f(x + y) = f(x) + f(y) - 1$ pro všechna nenulová $x,y,x+y$ .

Tonda Le | org | 3. 7. 2015 06:00:50

Ahoj,
také chci přispět k maratonu.
Řešení 3.úlohy+ skrytý text

Uvažujme $\textstyle S_A,S_B,S_C$ Švrčkovy body oproti vrcholům $\textstyle A,B,C$ . Snadno vyúhlíme, že $\textstyle S_AS_B$ je kolmá na $\textstyle CI$ , a proto $\textstyle S_AS_B \parallel LM$ . Analogicky odvodíme dvě další podobné rovnoběžnosti, tudíž $\textstyle KLM$ a $\textstyle S_AS_BS_C$ jsou stejnolehlé a v této stejnolehlosti se střed kružnice opsané $\textstyle KLM$ , bod $\textstyle I$ , se zobrazí na střed kružnice opsané $\textstyle S_AS_BS_C$ , bod $\textstyle O$ , a ortocentrum $\textstyle KLM$ , bod $\textstyle U$ , se zobrazí na ortocentrum $\textstyle S_AS_BS_C$ , bod $\textstyle I$ . Celkově dostaneme, že $\textstyle U,I,O$ leží na jedné přímce.

Zadání 4. úlohy:+ skrytý text

Najděte všechna reálná x taková, že \sqrt{5-x}=5-x^2

Štěpán Šimsa | org | 28. 6. 2015 00:12:19

Ahoj. Jen malé upřesnění k onomu řešení: + skrytý text

Pro využití AG nerovností potřebujeme, aby $o, p, q$ byla kladná čísla. Ale snadno vidíme, že maximálně jedno z nich je záporné a pak nerovnost před přepsáním do těchto proměnných triviálně platí, protože levá strana je záporná a pravá kladná.

Josef Svoboda | 26. 6. 2015 19:09:03

Ahoj, nějak se to řešení 2. úlohy rozsypalo. Tady je ještě jednou:
+ skrytý text

Podmínky $abc=1$ se ekvivaletně zbavíme substitucí $a=x/y$ , $b=y/z$ , $c=z/x$ . Nerovnost přejde do tvaru $(x-y+z)(y-z+x)(z-x+y) \leq xyz$ . Pro důkaz této nerovnosti vyjděme z nerovnosti $opq \leq \frac{o+p}{2} \frac{p+q}{2} \frac{q+o}{2}$ , která je součinem tří jednoduchých AG nerovností. Naši nerovnost z ní dostaneme dosazením $o=x-y+z$ , $p=y-z+x$ a $q=z-x+y$ .

<< < 1 2 ... 8 9 10 ... 36 37 > >>

Kontakt

email	info (zavináč) prase.cz
pošta	Matematický korespondenční seminář KAM MFF UK Malostranské náměstí 25 118 00 Praha 1

Organizátoři

Matematický korespondenční seminář je organizovaný studenty Matematicko-fyzikální fakulty UK pod záštitou Informatického ústavu UK a Oddělení propagace a mediální komunikace MFF UK.

Partneři

Realizace projektu byla podpořena Ministerstvem školství, mládeže a tělovýchovy

Matematický korespondenční seminář

Kalendář

Z naší fotogalerie

Kontakt

Organizátoři

Partneři