Marián Poppr | 15. 2. 2016 16:14:12
Ahoj,
právě přibyla tradiční várka nápověd k první jarní serii a k ní hinty pro druhou seriálovou serii:
první jarní serie
1. úloha+ skrytý text
2. úloha+ skrytý text
3. úloha+ skrytý text
4. úloha+ skrytý text
5. úloha+ skrytý text
6. úloha+ skrytý text
7. úloha+ skrytý text
8. úloha+ skrytý text
seriál
1. úloha+ skrytý text
2. úloha+ skrytý text
3. úloha+ skrytý text
právě přibyla tradiční várka nápověd k první jarní serii a k ní hinty pro druhou seriálovou serii:
první jarní serie
1. úloha+ skrytý text
Hraj si+ skrytý text
Existují tři způsoby
2. úloha+ skrytý text
Pro spor mějme dvě města, co nejsou propojena, existuje nutně mezi těmito dvěmi městy město, přes které můžeme mezi zvolenými městy cestovat?
3. úloha+ skrytý text
Ukaž, že se potkají právě jednou+ skrytý text
A to když Bára dožene Kubu+ skrytý text
Ještě by se mohli potkat uprostřed+ skrytý text
Sestav rovnici a zkoumej paritu
4. úloha+ skrytý text
Všimni si, že pokud by se Jerry k sýru nedostal hned v prvním tahu, tak mu Tom už vždy zabrání+ skrytý text
Stačí tedy, aby vždy existovaly právě dvě místnosti, mezi kterými není chodba
5. úloha+ skrytý text
Vezmi dvě místnosti A a B a nejkratší cestu délky s, poté pro libovolnou místnost (=C) mezi nimi, ukaž, že existují dvě cesty přes všechny místnosti o délce 3s+ skrytý text
Cesta C->A->B a C->B->A+ skrytý text
Je pak nejkratší cesta z C už určitě kratší než 1,5s?
6. úloha+ skrytý text
Pokud by se Štěpán s Filipem potkali v X, jak rychle by Viki prošel trasu A->B->X->C?+ skrytý text
A->B->X->C je delší než A->B->C, teď už to stačí jen dát dohromady a vysporovat
7. úloha+ skrytý text
Použij indukci a rozliš dva případy, pokud existuje org, který jde vždy s někým+ skrytý text
Pokud ano, odeberem ho a použijem indukci+ skrytý text
Pokud ne, vytvoř dvě skupiny (A,B) orgů, kde spolu orgové nikdy nešli.+ skrytý text
i. Vždy se podívej kdo z dané skupinky orgů došel nejdál
8. úloha+ skrytý text
Ukaž, že kdyby d a h nedávali stejný zbytek po dělení 4, tak že se David s Honzou zacyklí na cestě o délce 4dh a dál se nedostanou+ skrytý text
Podívej se, jak se pohybuje auto každých dh kilometrů+ skrytý text
Je patrné, že d a h musí dávat tedy zbytek 1 a 3 po dělení 4, zbývá tedy ukázat, že za prvních dh tahů se posune vždy o 1 kilometr po přímce mezi startem a cílem+ skrytý text
Nyní si můžeme například znázornit situaci do komplexní roviny kde se chceme dostat z (0,0) do (1,0) a o směrech (1,i,-1,-i). Zvolme si například variantu kdy d a h dávají zbytek 1, pak chcem ukázat že součet směrů je roven jedné, nebo-li součet mk:=(-i)^(k div h) i^(k div d) pro k od 0 do kh-1+ skrytý text
Uprav mk jako (-i)^(ak) i^(bk) (kde ak a bk jsou zbytky po dělení k čísly h a d), zbytek dořeš čínskou zbytkovou větou+ skrytý text
i. Dvojici (ak,bk) odpovídá (k mod h, k mod d)
seriál
1. úloha+ skrytý text
Tvrzení říká, že ke každé množině A existuje množina B, která obsahuje všechny podmnožiny množin náležících A+ skrytý text
Vytvoř si podmnožinu každého prvku A+ skrytý text
Použij axiom potence a schéma axiomu nahrazení+ skrytý text
Zbytek dořeš axiomem sjednocení
2. úloha+ skrytý text
Zobraz lokalní maximum x do dvojice racionálních čísel+ skrytý text
x je v prvek z intervalu (a,b), kde f(x)<f(c) pro všechny c z (a,b) různá od x. Jak tedy najdeme hledaná rac. čísla?+ skrytý text
Mezi každými dvěmi reálnými čísli je alespoň jedno rac. tedy i mezi a a x a b a x
3. úloha+ skrytý text
Nejprve zkoumej, jak velké bude sjednocení spočetné množiny spočetných ordinálů+ skrytý text
Což je spočetný ordinál+ skrytý text
+ skrytý text
+ skrytý text Použij definici suprema
+ skrytý text
Zkoumej, jak velké bude supremum nejmenší spočetné podmnožiny X (=Nx)+ skrytý text
Použij transfinní indukci a dokaž, že lib. Konečný ordinál větší než supremum N náleží do X
Konečně ukaž, že průnik dvou šikovných množin X a Y bude nespočetný, tedy bude obsahovat všechny spočetné ordinály větší než max(sup(Nx,Ny))+ skrytý text
Podmínka ii už není příliš obtížná :)
Evžen Wybitul | 4. 2. 2016 08:06:45
Dobře, příště si dam pozor. Promiň a díky za odpověď :)
E.T. | org | 3. 2. 2016 04:24:14
Ahoj Evžene,
Tom umísťuje Jerryho i sýr sám dle vlastního výběru. Příště se nás ale, prosím, ptej na nejasnosti k aktuálním úlohám pomocí e-mailu (mks (zavináč) mff.cuni.cz). (V sekci chatu "Pokec" je tato výzva dokonce zvýrazněna.) Nechceme účastníky zbytečně otravovat a omezovat v používání chatu, ale špatně položený dotaz by mohl ostatním prozradit řešení. Tvůj dotaz je celkem nevinný, takže se nic neděje, ale příště nám pro jistotu piš na e-mail.
Hodně štěstí při řešení!
Tom umísťuje Jerryho i sýr sám dle vlastního výběru. Příště se nás ale, prosím, ptej na nejasnosti k aktuálním úlohám pomocí e-mailu (mks (zavináč) mff.cuni.cz). (V sekci chatu "Pokec" je tato výzva dokonce zvýrazněna.) Nechceme účastníky zbytečně otravovat a omezovat v používání chatu, ale špatně položený dotaz by mohl ostatním prozradit řešení. Tvůj dotaz je celkem nevinný, takže se nic neděje, ale příště nám pro jistotu piš na e-mail.
Hodně štěstí při řešení!
Evžen Wybitul | 1. 2. 2016 21:57:35
Ahoj
Moc mi není jasné zadání úlohy číslo 4 z první jarní série (Tom a Jerry). Umisťuje Tom sýr i Jerryho sám, nebo je jejich umístění náhodné?
Díky
Moc mi není jasné zadání úlohy číslo 4 z první jarní série (Tom a Jerry). Umisťuje Tom sýr i Jerryho sám, nebo je jejich umístění náhodné?
Díky
Daniel Herman | 31. 1. 2016 23:49:38
Ďakujem :)
Miroslav Olšák | org | 31. 1. 2016 18:59:38
Tohle je nahlížecí úloha, přečtu a vidím, že to platí, žádné převádění na jiné vzorečky :-)
Konkrétně tedy příklad 2: Máš dvě n-prvkové hromádky bílých kamínků. Tak to, že si z nich dohromady vezmeš m kamínků znamená, že si jich z první vezmeš nějaké k a z druhé n-k.
Konkrétně tedy příklad 2: Máš dvě n-prvkové hromádky bílých kamínků. Tak to, že si z nich dohromady vezmeš m kamínků znamená, že si jich z první vezmeš nějaké k a z druhé n-k.
Daniel Herman | 31. 1. 2016 16:18:08
Pýtam nejakú dobrú dušu o pomoc. Z knižnice - Počítání dvěma způsoby - Príklad 2. http://mks.mff.cuni.cz/library/Pocitani2Zpuso... Viem, že

ale ďalej sa dostať neviem.
Za každú pomoc ďakujem.
ale ďalej sa dostať neviem.
Za každú pomoc ďakujem.
David Hruška | org | 25. 1. 2016 23:33:54
Adam: Jasně, napiš mi na d.hruska@centrum.cz.
Adam | 24. 1. 2016 20:27:10
Zdravím poradil by mi tu někdo z příkladem soustavy rovnic o dvou neznámých ?
Miroslav Olšák | org | 21. 1. 2016 19:43:22
Slíbil jsem nápovědu k čokoládové výzvě ze seriálu, zde je:
(1) Hodí se vědět, že pro nekonečnou množinu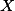 platí
platí  . K dokázání tohoto tvrzení pro množiny, kde to je potřeba žádná teorie nechybí, ale je trochu technické, tak jeho důkaz nebudu vyžadovat.
. K dokázání tohoto tvrzení pro množiny, kde to je potřeba žádná teorie nechybí, ale je trochu technické, tak jeho důkaz nebudu vyžadovat.
(2) Návodná úloha: Dokažte, že množinu lze obarvit spočetně mnoha barvami tak, aby se v ní nevyskytoval jednobarevný obdélník, zatímco množinu
lze obarvit spočetně mnoha barvami tak, aby se v ní nevyskytoval jednobarevný obdélník, zatímco množinu  tak již obarvit nelze. Obdélníkem (či přesněji vrcholy obdélníka) rozumíme obecnou čtyřprvkovou množinu tvaru
tak již obarvit nelze. Obdélníkem (či přesněji vrcholy obdélníka) rozumíme obecnou čtyřprvkovou množinu tvaru  , kde
, kde  jsou dvouprvkové množiny.
jsou dvouprvkové množiny.
Připomínám, že řešení čokoládové výzvy k seriálu se posílá na můj e-mail uvedený v seznamu organizátorů. Tak neváhejte, čokolád je zatím dost (i s iKS dohromady 9), ale časem ubudou... Buď první, kdo to vyřeší!
(1) Hodí se vědět, že pro nekonečnou množinu
(2) Návodná úloha: Dokažte, že množinu
Připomínám, že řešení čokoládové výzvy k seriálu se posílá na můj e-mail uvedený v seznamu organizátorů. Tak neváhejte, čokolád je zatím dost (i s iKS dohromady 9), ale časem ubudou... Buď první, kdo to vyřeší!
Michal Buráň | 19. 1. 2016 16:42:59
Otevřelo se přihlašování na matematický tábor pro středoškoláky PROMYS Europe http://promys-europe.org/. Letos se podruhé koná v Oxfordu podle bostonského modelu, kde byl už 27x. Jako nová akce není příliš známý.
Je to šest týdnů intenzivní matiky. Jádro programu tvoří přednášky z teorie čísel a denní sada úloh. Na začátku se nepředpokládají žádně neobyčejné znalosti. Závěr kurzu se věnuje kvadratické reciprocitě.
Každý student si navíc zvolí "exploration project", který simuluje matematický výzkum. Ve trojicích se společně s jedním orgem snaží vyřešit v průběhu tábora obtížný matematický problém. Podobně jako v profesionální vědě je součástí projektu i formulace vlastních otázek a domněnek. Projekty mají záměrně otevřený konec a mnoho možných směřování. Své objevy účastníci sepíší a prezentují ostatním.
Aspoň jednou týdně máme pozvaného přednášejího hosta. Často jsou to matematici v různých fázích akademické kariéry. Loni mezi nimi byl i Andrew Wiles.
Oproti soustředkám je tam daleko víc matiky a míň sportů a her.
A chtěl bych zdůraznit, že: "Full and partial need-based financial aid is also available. PROMYS Europe is dedicated to the principle that no student should be unable to attend for financial reasons."
A neváhejte se mě na cokoli o PROMYSu zeptat. nebo napište Nině Hronkovičové, která se loni zúčastnila.
Je to šest týdnů intenzivní matiky. Jádro programu tvoří přednášky z teorie čísel a denní sada úloh. Na začátku se nepředpokládají žádně neobyčejné znalosti. Závěr kurzu se věnuje kvadratické reciprocitě.
Každý student si navíc zvolí "exploration project", který simuluje matematický výzkum. Ve trojicích se společně s jedním orgem snaží vyřešit v průběhu tábora obtížný matematický problém. Podobně jako v profesionální vědě je součástí projektu i formulace vlastních otázek a domněnek. Projekty mají záměrně otevřený konec a mnoho možných směřování. Své objevy účastníci sepíší a prezentují ostatním.
Aspoň jednou týdně máme pozvaného přednášejího hosta. Často jsou to matematici v různých fázích akademické kariéry. Loni mezi nimi byl i Andrew Wiles.
Oproti soustředkám je tam daleko víc matiky a míň sportů a her.
A chtěl bych zdůraznit, že: "Full and partial need-based financial aid is also available. PROMYS Europe is dedicated to the principle that no student should be unable to attend for financial reasons."
A neváhejte se mě na cokoli o PROMYSu zeptat. nebo napište Nině Hronkovičové, která se loni zúčastnila.
Radovan Švarc | 18. 1. 2016 20:22:11
Čaute
Máte rádi matiku? Máte rádi iKSko? Máte rádi ČOKOLÁDU!?!?!?! Pokud jste alespoň na jednu otázku odpověděli "ano", "hmm", "jo", nebo "hej", čtěte dál. (V opačném případě taky.)
Už dvakrát v minulosti jste mohli být svědky souboje Čechů proti Slovákům v rámci Velkých cen iKS. Obě zápolení zatím vyhráli Slováci, ale letos může být všechno jinak. O co jde?
Pravidla jsou jednoduchá -- stačí vyřešit úlohu z letošní sedmé série iKS, podívat se na stránku Velké ceny (http://iksko.org/velkeceny.php), který organizátor ji má na starosti a poslat mu mail, ve kterém se ho pokusíte přesvědčit, že jste ji opravdu vyřešili (ačkoli nemusíte zabíhat do všech podrobností). Za to pak (pokud ho přesvědčíte) kromě imaginární Velké ceny za Velkou úlohu vyhráváte navíc 2^(1-n) čokolády, kde n je pořadí, ve kterém jste danou úlohu vyřešili. Celkem se tak rozdá skoro 8 čokolád, přičemž hypotetické maximum pro jednoho řešitele jsou až 4 čokolády!
Na stránce Velké ceny (http://iksko.org/velkeceny.php) se navíc bude počítat česko-slovenské skóre -- Nejprve pro každou úlohu zvlášť a pak celkové podle toho, kdo vede na kolika úlohách.
Pokud nemůžete na stránkách najít zadání 7. série, je to v pořádku. Zadání totiž zveřejníme až o půlnoci -- po termínu odeslání 6. série.
GL&HF
P.S.: Pokud plánujete úlohu skutečně poslat s tím, aby se objevila i nakonec ve výsledovce, potom pozor -- v rámci velkých cen stačí napsat řešení emailem příslušnému organizátorovi, ale před termínem odeslání je stále potřeba řešení sepsat a poslat submitovátkem/poštou jako obvykle. Pokud vám ale jde jen o Velké ceny (http://iksko.org/velkeceny.php), potom skutečně stačí jen email příslušnému orgovi.
Máte rádi matiku? Máte rádi iKSko? Máte rádi ČOKOLÁDU!?!?!?! Pokud jste alespoň na jednu otázku odpověděli "ano", "hmm", "jo", nebo "hej", čtěte dál. (V opačném případě taky.)
Už dvakrát v minulosti jste mohli být svědky souboje Čechů proti Slovákům v rámci Velkých cen iKS. Obě zápolení zatím vyhráli Slováci, ale letos může být všechno jinak. O co jde?
Pravidla jsou jednoduchá -- stačí vyřešit úlohu z letošní sedmé série iKS, podívat se na stránku Velké ceny (http://iksko.org/velkeceny.php), který organizátor ji má na starosti a poslat mu mail, ve kterém se ho pokusíte přesvědčit, že jste ji opravdu vyřešili (ačkoli nemusíte zabíhat do všech podrobností). Za to pak (pokud ho přesvědčíte) kromě imaginární Velké ceny za Velkou úlohu vyhráváte navíc 2^(1-n) čokolády, kde n je pořadí, ve kterém jste danou úlohu vyřešili. Celkem se tak rozdá skoro 8 čokolád, přičemž hypotetické maximum pro jednoho řešitele jsou až 4 čokolády!
Na stránce Velké ceny (http://iksko.org/velkeceny.php) se navíc bude počítat česko-slovenské skóre -- Nejprve pro každou úlohu zvlášť a pak celkové podle toho, kdo vede na kolika úlohách.
Pokud nemůžete na stránkách najít zadání 7. série, je to v pořádku. Zadání totiž zveřejníme až o půlnoci -- po termínu odeslání 6. série.
GL&HF
P.S.: Pokud plánujete úlohu skutečně poslat s tím, aby se objevila i nakonec ve výsledovce, potom pozor -- v rámci velkých cen stačí napsat řešení emailem příslušnému organizátorovi, ale před termínem odeslání je stále potřeba řešení sepsat a poslat submitovátkem/poštou jako obvykle. Pokud vám ale jde jen o Velké ceny (http://iksko.org/velkeceny.php), potom skutečně stačí jen email příslušnému orgovi.
Miroslav Olšák | org | 14. 1. 2016 21:06:23
Tak když jste se popasovali s krajským kolem, nezapomeňte na seriál ;-)
Vím, že je to netriviální téma. Rád tedy tady na chatu zodpovím jakékoli dotazy k seriálu, krom těch, které by se přímo týkaly řešení 2. série seriálových úloh nebo 2. čokoládové výzvy.
Čokoládovou výzvu zatím nikdo nevyřešil. Rozhodl jsem se tedy, že za týden -- ve čtvrtek 21. 1. zveřejním drobnou nápovědu, která sice neodkryje klíčové myšlenky řešení, ale pomůže s technickými obtížemi.
P.S. Oba odstavce se sice týkají primárně řešitelů, ale ne jenom jich. I pro organizátory probíhá soutěž o čokolády, zapoj se ;-)
Vím, že je to netriviální téma. Rád tedy tady na chatu zodpovím jakékoli dotazy k seriálu, krom těch, které by se přímo týkaly řešení 2. série seriálových úloh nebo 2. čokoládové výzvy.
Čokoládovou výzvu zatím nikdo nevyřešil. Rozhodl jsem se tedy, že za týden -- ve čtvrtek 21. 1. zveřejním drobnou nápovědu, která sice neodkryje klíčové myšlenky řešení, ale pomůže s technickými obtížemi.
P.S. Oba odstavce se sice týkají primárně řešitelů, ale ne jenom jich. I pro organizátory probíhá soutěž o čokolády, zapoj se ;-)
Štěpán Šimsa | org | 12. 1. 2016 15:52:41
Taky se mi úlohy moc nelíbí, akorát dvojka je fajn. Na postup tipuju 12 bodů.
Danil | 12. 1. 2016 15:06:42
Jo, beru svá slova o dvojce zpět, to jen já jsem zabiják geometrií :D
Když tak vzoráky už jsou na http://skmo.sk/dokument.php?id=1732
Když tak vzoráky už jsou na http://skmo.sk/dokument.php?id=1732
Lucien Šíma | 12. 1. 2016 14:59:50
Dvojku jsem udělal podobností a pythagorovou větou... a to prý existuje ještě hezčí řešení
Lucien Šíma | 12. 1. 2016 14:57:52
Mně se úlohy taky moc nelíbily (i když dvojka byla podle mě celkem pěkná). Snad mám taky všechno a hranici tipuju na něco kolem 18 bodů...
Danil | 12. 1. 2016 14:55:25
Ahoj všichni, já budu trochu větší optimista a tipnu hranici na 15-16 bodů, neboli 2.5 úlohy.
Jednička byla taková poměrně přímočará, ale přesto poměrně hezká, i když na mě asi příliš numerického počítán.
Dvojka byla fakt odporně nechutná, nebo alespoň zatím neznám žádné hezké řešení... Přišli jste někdo na něco hezčího, než sinovka a pak Jensen+AG (respektive místo toho derivace), Jensen na divnou funkci, nebo hardcore analytika?
Trojka nějak moc lehká, proto taky ten vysoký bodový odhad, v podstatě jedna úloha byla fakt zadarmo.
Čtyřka mi jako jediná dala celkem zabrat, taky se mi ze všeho nejvíc líbila, snad jsem i přišel na to trikovější řešení bez jakékoliv mlhy :D
Jinak se mi dařilo celkem dobře, doufám v plný počet :)
Co vy ostatní?
Jednička byla taková poměrně přímočará, ale přesto poměrně hezká, i když na mě asi příliš numerického počítán.
Dvojka byla fakt odporně nechutná, nebo alespoň zatím neznám žádné hezké řešení... Přišli jste někdo na něco hezčího, než sinovka a pak Jensen+AG (respektive místo toho derivace), Jensen na divnou funkci, nebo hardcore analytika?
Trojka nějak moc lehká, proto taky ten vysoký bodový odhad, v podstatě jedna úloha byla fakt zadarmo.
Čtyřka mi jako jediná dala celkem zabrat, taky se mi ze všeho nejvíc líbila, snad jsem i přišel na to trikovější řešení bez jakékoliv mlhy :D
Jinak se mi dařilo celkem dobře, doufám v plný počet :)
Co vy ostatní?
Jan Petr | 12. 1. 2016 13:57:41
Popravdě se mi úlohy moc nelíbily (ale možná jsem minul nějaké hezké řešení – věřím, že u dvojky něco hezčího bylo – což by mě mrzelo)... Nějak jsem je nakonec všechny vyřešil (a výsledky souhlasí s těmi od Danila), ale vysvětlení (zvláště čtyřky) může být místy mlhavé. Hranici tipnu na 13 bodů, pro začátek.
Lucien Šíma | 12. 1. 2016 13:36:46
Co říkate na krajské kolo áčka? Jak se vám dařilo? Kolik tipujete bodů potřebných na postup? ;)





