Michal Beránek | 21. 7. 2018 19:35:17
Ahoj prosím, jak vyexportuju soubor v Texmakeru do pdf? Náhled vidím, ale nevím, jak získat pdf soubor. Zkoušel jsem pdfLatex (F6), ale ukládá se mi prázdné pdf. HELP PLEASE!
Olin | org | 31. 5. 2018 01:18:12
Náhodou jsem po delší době proklikl stránky PraSete, pročež jsem zjistil, že téma seriálu je teorie grup… Co se týče otázky v poznámkách k řešení dvojky (zda podgrupa součinu je izomorfní součinu podgrup), tak podle mě ano pro konečné (konečně generované) grupy čistě z jejich klasifikace, pro nekonečně generované typicky ne.
OndraD | 11. 5. 2018 12:40:42
Ahojte, nesouvisí to přímo s PraSetem, ale letošní konstrukční úloha z Matematiky+ šla krásně zabít použitím Švrčkova bodu. :))
David Hruška | org | 22. 4. 2018 01:46:32
Ahoj, další TriKS začíná už za pár minut! Změřte své síly s ostatními během dvou hodin na pěti úlohách na http://iksko.org/triks/current.php.
madam Verča | 10. 3. 2018 08:41:11
Ahoj!
hinty k 2. jarní sérii zde :
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5. + skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
hinty k 2. jarní sérii zde :
Úloha 1.+ skrytý text
16 a 8 musí být na začátku a na konci.
Úloha 2.+ skrytý text
Z odstřižků doskládej další čtverečky.
Úloha 3.+ skrytý text
Rozděl na obdélníky 3x2.
Úloha 4.+ skrytý text
Porovnejte počet možných vzdáleností a počet dvojic.
Úloha 5. + skrytý text
Můžeme si představit, že Kuba kostkami nejprve hodí a teprve potom náhodně vylosuje čísla z klobouku a nalepí je na stěny kostky.
Úloha 6.+ skrytý text
Jaký je součet čísel nad diagonálou?
Úloha 7.+ skrytý text
Máme hyperkrychli, dáme si do grafu ty hrany které spojují vybrané vrcholy. V grafu vezmeme maximální kostru. Ta má max n-1 hran. Tedy v nějakém směru není hrana.
Úloha 8.+ skrytý text
Filip vyhraje pro každé n.+ skrytý text
Podívejte se na projekce na osy, resp. průniky s osami.+ skrytý text
Dokažte si indukcí podle d. pomocné lemma: pro libovolné n, d a l umí Filip vyrobit l skupinek d červených krychliček, jejichž projekce na jednu z os jsou disjunktní, vzdálené alespoň 2n+1 od sebe i od průniku libovolné modré plochy s touto osou.
madam Verča | 16. 2. 2018 01:34:28
První jarní hinty letošního ročníku již spatřili světlo světa! A s nima i hinty k 2. seriálové sérii.
1. jarní série
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text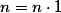
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
2. seriálová série
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
1. jarní série
Úloha 1.+ skrytý text
Jak to vypadá ve chvíli, kdy oba týmy daly dohromady osm gólů?
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Tři body položce na přímku a čtvrtý mimo takovým způsobem, aby všechny trojúhelníky byly rovnoramenné.
Úloha 4.+ skrytý text
Rozdělte pracovní dobu na půlky, půlky půlek, půlky půlek půlek, ... a rozdělte lidi odpovídajícím způsobem do nich.
Úloha 5.+ skrytý text
Hamlet se nikdy nezastaví, takže se časem objeví v situaci, ve které už někdy byl.+ skrytý text
Rozmyslete si, že umíme po každém kroku určit, jak vypadala situace před tímto krokem.
Úloha 6.+ skrytý text
Předpokládejte, že posloupnost existuje a ukažte, že posloupnost je rostoucí a z toho, že všechny její členy jsou menší než 1. Následně uvažte součet prvních  členů.
členů.
Úloha 7.+ skrytý text
Vezměte za  čtverec, za
čtverec, za 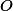 střed čtverce. Rozpůlme
střed čtverce. Rozpůlme  na dva trojúhelníky libovolnou jeho úhlopříčkou a uvažujme trojúhelník
na dva trojúhelníky libovolnou jeho úhlopříčkou a uvažujme trojúhelník 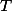 , který vznikne tím, že jeden z takto vzniklých trojúhelníků nafoukneme na dvojnásobek stejnolehlostí z bodu
, který vznikne tím, že jeden z takto vzniklých trojúhelníků nafoukneme na dvojnásobek stejnolehlostí z bodu 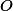 . Nakonec zvolme
. Nakonec zvolme  jako "skoro"
jako "skoro" 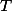 .
.
Úloha 8.+ skrytý text
Nechť 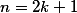 . Zvolme všechna
. Zvolme všechna 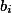 rovna jedné a
rovna jedné a 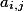 rovna mínus jedné pokud zbytek
rovna mínus jedné pokud zbytek 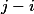 po dělení
po dělení  je menší než
je menší než 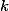 . Abyste ukázali, že toto funguje, ukažte, že kdykoliv je
. Abyste ukázali, že toto funguje, ukažte, že kdykoliv je 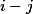 kongruentní
kongruentní 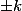 modulo
modulo  , tak alespoň jedno z čísel
, tak alespoň jedno z čísel 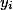 a
a 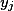 je rovno
je rovno 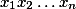 .
.
2. seriálová série
Úloha 1.+ skrytý text
Pokud si vybereme jednu stěnu kostky, máme 6 možností, na kterou jinou stěnu ji zobrazit, posléze máme 4 možnosti, jak ji pootočit, příslušná grupa G má tedy 24 prvků.+ skrytý text
Rozmyslete si, jakým způsobem prvky grupy G permutují stěny krychle a příklad dokončete Burnsideoým lematem.
Úloha 2.+ skrytý text
Z prvních dvou vlastností je jasné, že f je permutace tvořená samými dvojcykly. Číslo  je proto sudé.+ skrytý text
je proto sudé.+ skrytý text
Zobrazení 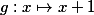 je také permutce, která je díky sudosti n lichá.+ skrytý text
je také permutce, která je díky sudosti n lichá.+ skrytý text
Ze třetí podmínky a multiplikativity znaménka určete paritu permutace f. Pak už je díky cyklové struktuře f vše jasné."
Úloha 3.+ skrytý text
Předpokládejte pro spor, že jich existuje víc, a použijte vlastnost ze zadání pro normalizátor jedné sylowovské p-podgrupy.
madam Verča | 16. 2. 2018 01:33:52
Ahoj!
Už i poslední podzimní série má své hinty!
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text musí být prvočíslo a pak pracujte modulo
musí být prvočíslo a pak pracujte modulo 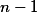 .
.
Úloha 8.+ skrytý text
Už i poslední podzimní série má své hinty!
Úloha 1.+ skrytý text
Co lze odebrat, lze taky přidat.
Úloha 2.+ skrytý text
Uvažujte zbytky po dělení třemi.
Úloha 3.+ skrytý text
Jak se dá 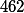 zapsat jako součet dvou svých dělitelů?
zapsat jako součet dvou svých dělitelů?
Úloha 4.+ skrytý text
Využijte kritérium pro dělitelnost jedenácti.
Úloha 5.+ skrytý text
Zkoumejte paritu.
Úloha 6.+ skrytý text
Jen jedna z množin může mít víc než jeden prvek.+ skrytý text
Uvažujme kterýkoli prvek, který nepatří do oné jednoprvkové množiny. Co lze říct o menších číslech?
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
Nejprve si ke každému políčku přiřaďte unikátní prvočíslo. Pomocí nich si zajistěte druhou podmínku, bez ohledu na první. Nyní zvolte dostatečně velké prvočíslo P, nesoudělné se všemi prozatím napsanými čísly a vynásobte každé políčko takovým koeficientem, aby součet v každém dominu byl P.
madam Verča | 16. 2. 2018 01:32:53
Milá PraSátka,
další měsíc již uběhl a zde jsou hinty ke dvoum dalším sériím!
3. podzimní série
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
1. seriálová série
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text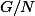 nekonečná cyklická je izomorfmí se
nekonečná cyklická je izomorfmí se 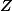 (celá čísla se sčítáním), takže z ní vede surjektivní homomorfismus do
(celá čísla se sčítáním), takže z ní vede surjektivní homomorfismus do 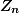 (celá čísla modulo n) daný dělením se zbytkem.+ skrytý text
(celá čísla modulo n) daný dělením se zbytkem.+ skrytý text
další měsíc již uběhl a zde jsou hinty ke dvoum dalším sériím!
3. podzimní série
Úloha 1.+ skrytý text
Co třeba rovnoběžné s nějakou stranou ?
Úloha 2.+ skrytý text
Spočítejte úhel u vrcholu  .
.
Úloha 3.+ skrytý text
Použijte kružnice vepsané.
Úloha 4.+ skrytý text
Může Rado zašlápnout Michala?
+ skrytý text
+ skrytý text
Obarvěte šachovnicově políčka.
Úloha 5.+ skrytý text
Úhlete pomocí velikostí oblouků na kružnici.
Úloha 6.+ skrytý text
Dokresli si rovnoběžky se stranami procházející  .
.
Úloha 7.+ skrytý text
Překlopte 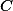 podle osy strany
podle osy strany 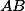 , čímž získáte čtvrtý bod lichoběžníku
, čímž získáte čtvrtý bod lichoběžníku 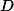 . + skrytý text
. + skrytý text
S využitím zadané podmínky na úhly nahlédněte, že tři strany tohoto lichoběžníku jsou stejně dlouhé.+ skrytý text
Trojúhelník 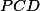 je rovnostranný.+ skrytý text
je rovnostranný.+ skrytý text
Dopočtěte.
Úloha 8.+ skrytý text
Přímky 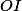 a
a 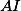 protínají
protínají 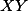 pod stejným úhlem.
pod stejným úhlem.
1. seriálová série
Úloha 1.+ skrytý text
Chceme 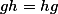 pro všechna
pro všechna 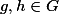 . Rozmyslete si, že
. Rozmyslete si, že 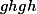 a
a 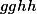 se rovnají.
se rovnají.
Úloha 2.+ skrytý text
Každé racionální číslo se dá zapsat jednoznačně jako součin prvočísel umocněných na celočíselné exponenty.
Úloha 3.+ skrytý text
Jádro tohoto homomorfismu je podgrupa grupy 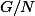 tvaru
tvaru 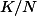 pro nějakou
pro nějakou 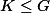 . Podle první a druhé věty o izomorfismu je potom
. Podle první a druhé věty o izomorfismu je potom 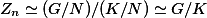 , tedy tato
, tedy tato 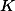 má v
má v 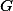 index
index  .
.
madam Verča | 8. 11. 2017 20:52:17
Ahoj ahoj!
tady je další várka hintů, tentokrát k 2. podzimní sérii ;)
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
tady je další várka hintů, tentokrát k 2. podzimní sérii ;)
Úloha 1.+ skrytý text
Když jsou vedle osmičky čtyřky, nemusí být ta osmička číslice nějakého dvouciferného čísla? Jaká čísla to mohou být?
Úloha 2.+ skrytý text
Jak se dají získat malé součty?
Úloha 3.+ skrytý text
Kolik existuje uspořádaných čtveřic čísel z množiny 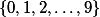 takových, že jejich součet je dělitelný třemi?
takových, že jejich součet je dělitelný třemi?
Úloha 4.+ skrytý text
Kolika způsoby lze umístit 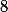 věží na jednu barvu, aby se neohrožovaly?+ skrytý text
věží na jednu barvu, aby se neohrožovaly?+ skrytý text
Na šachovnici 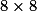 by šlo
by šlo 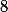 věží umístit
věží umístit 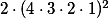 způsoby (tak, aby v každém rozmístění byly pouze na jedné barvě).
způsoby (tak, aby v každém rozmístění byly pouze na jedné barvě).
Úloha 5.+ skrytý text
Zkus si označit  počet druháků a
počet druháků a 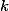 počet bodů, které získal každý z nich. Potom lze zadání přepsat do rovnice (napovím, že celkem bylo rozdáno
počet bodů, které získal každý z nich. Potom lze zadání přepsat do rovnice (napovím, že celkem bylo rozdáno 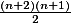 bodů), ze které vyplyne, že počet druháků musí být dělitelem
bodů), ze které vyplyne, že počet druháků musí být dělitelem 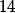 .
.
Úloha 6.+ skrytý text
Kolikrát se započítá jeden konkrétní prvek množiny 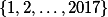 do hledaného součtu?+ skrytý text
do hledaného součtu?+ skrytý text
Když umístíme jeden prvek do průniku 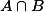 , máme přesně čtyři možnosti, kam dát libovolný další prvek: do
, máme přesně čtyři možnosti, kam dát libovolný další prvek: do 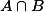 ,
, 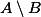 ,
, 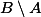 , nebo do
, nebo do 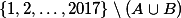 .
.
Úloha 7.+ skrytý text
Součin faktoriálů stupňů vrcholů.
Úloha 8.+ skrytý text
Kolika způsoby můžete obarvit náhrdelník o  kamíncích
kamíncích 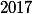 barvami tak, aby se při žádném netriviálním pootočení nepřenesl na stejně vypadající?
barvami tak, aby se při žádném netriviálním pootočení nepřenesl na stejně vypadající?
madam Verča | 29. 10. 2017 22:45:16
Ahoj!
Nepodařilo se ti vyřešit nějakou úlohu z 1. podzimní série a nemůžeš se dočkat vzorových řešení ? Pak tady máš pár hintů a můžeš se o to znovu pokusit mimo soutěž :)
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text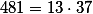 + skrytý text
+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
Nepodařilo se ti vyřešit nějakou úlohu z 1. podzimní série a nemůžeš se dočkat vzorových řešení ? Pak tady máš pár hintů a můžeš se o to znovu pokusit mimo soutěž :)
Úloha 1.+ skrytý text
Zeptej se postupně na 16 trojic krabiček a zbylou dvojici vyřeš samostatně. + skrytý text
Zbylou dvojici krabiček dosaď po jedné do známé trojice.
Úloha 2.+ skrytý text
Vepiš stůl do čtverce, a ten čtverec rozděl na malé čtverce o velikosti plácačky. + skrytý text
Použij Dirichletův princip.
Úloha 3.+ skrytý text
Kdyby ciferný součet šestkrát za sebou vzrostl o jedna, musí jednou být dělitelný 7. + skrytý text
Kromě případů, kdy se přechází přes desítku, se nemůže ciferný součet změnit jinak než zvětšit o jedna.
Úloha 4.+ skrytý text
Použij Dirichletův princip.
Úloha 5.+ skrytý text
V důkazu potřebujeme využít dvě věci: + skrytý text
Najít dvojici po sobě jdoucích ptakopysků, mezi kterými je největší mezera.
+ skrytý textOrientovat si kružnici.
Úloha 6.+ skrytý text
Pro lichá n: rozmístěte 2x2 čtverce tak aby jste právě n políček buď nezahrnuli do žádného čtverce nebo zahrnuli do dvou čtverců. + skrytý text
Tato políčka budou na diagonále.
Úloha 7.+ skrytý text
Řešte indukcí. + skrytý text
Najděte řešení, kde každý další prvek bude roven součinu předchozích - někdy zmenšený o jedna, někdy zvětšený o jedna.
Úloha 8.+ skrytý text
Dokreslete si kružnice opsané ABD a CBD. Ukažte, že EA a EC se jich dotýkají. + skrytý text
Označte X a Y průsečíky těchto kružnic s l.
Miroslav Olšák | org | 30. 9. 2017 21:13:39
Ahoj, první díl seriálu "Do nekonečna a ještě dál" se dočkal video verze. Nechť se líbí :-)
https://www.youtube.com/playlist?list=PL2m0Oz...
Snad se někdy dostanu i na zbytek...
https://www.youtube.com/playlist?list=PL2m0Oz...
Snad se někdy dostanu i na zbytek...
Jakub Krásenský | org | 1. 7. 2017 21:08:33
Ahoj!
Byli jste napjatí, o čem bude v příštím ročníku seriál? Teď vám to řekneme, abyste se mohli začít těšit (nebo psychicky připravovat):
V letošním seriálu vás provedeme velmi zajímavou oblastí matematiky: teorií grup. Jedná se o rozsáhlou teorii s rozmanitými důsledky v mnoha odvětvích; v seriálu se budeme zabývat jejími základními aspekty a podíváme se na některá hezká využití. Abstraktní přístup, který je dnes běžný, pochází až z devatenáctého století a umožňuje nám popisovat základní vlastnosti mnoha pravidelných objektů naráz. Vybudovaná teorie má přitom navzdory své obecné formulaci mnoho pěkných, hravých a velmi konkrétních důsledků například v kombinatorice nebo teorii čísel, a umožňuje nám tak lépe pochopit, jak spolu různé oblasti matematiky souvisí.
Byli jste napjatí, o čem bude v příštím ročníku seriál? Teď vám to řekneme, abyste se mohli začít těšit (nebo psychicky připravovat):
V letošním seriálu vás provedeme velmi zajímavou oblastí matematiky: teorií grup. Jedná se o rozsáhlou teorii s rozmanitými důsledky v mnoha odvětvích; v seriálu se budeme zabývat jejími základními aspekty a podíváme se na některá hezká využití. Abstraktní přístup, který je dnes běžný, pochází až z devatenáctého století a umožňuje nám popisovat základní vlastnosti mnoha pravidelných objektů naráz. Vybudovaná teorie má přitom navzdory své obecné formulaci mnoho pěkných, hravých a velmi konkrétních důsledků například v kombinatorice nebo teorii čísel, a umožňuje nám tak lépe pochopit, jak spolu různé oblasti matematiky souvisí.
David Hruška | org | 20. 5. 2017 02:11:08
Ahoj Michale, jednak je něco v seriálu (http://mks.mff.cuni.cz/commentary/C/serie2s/u...), pak třeba na http://www.talnet.cz/documents/18/17100201-b6... a pak třeba náhodná úloha, co mě napadá: Máš tětivový čtyřúhelník a spojíš středy protějších oblouků (tedy nějaké body Š_a a Š_c). Dokaž, že tyto dvě spojnice jsou na sebe kolmé.
Marián Poppr | 17. 5. 2017 20:34:43
Ahoj,
již i letošní závěrečná série má své hinty:
Úloha 1a)+ skrytý text
Úloha 1b)+ skrytý text
Úloha 2a)+ skrytý text
Úloha 2b)+ skrytý text
Úloha 3a)+ skrytý text
Úloha 3b)+ skrytý text
Úloha 4a)+ skrytý text
Úloha 4b)+ skrytý text
Úloha 5a)+ skrytý text
Úloha 5b)+ skrytý text
Úloha 6a)+ skrytý text
Úloha 6b)+ skrytý text
Úloha 7a)+ skrytý text
Úloha 7b)+ skrytý text
již i letošní závěrečná série má své hinty:
Úloha 1a)+ skrytý text
Má tabulka sloupec s různými čísly? A když ne, tak skus přeuspořádat nějaké tři sloupce.
Úloha 1b)+ skrytý text
Nepodaří.
+ skrytý text
+ skrytý text
Vezmi si tabulku vyplněnou jen  jedničkami a zbytek nulami. Jakých součtů mohou nabývat řádky a sloupce a jak by mohly nasčítat
jedničkami a zbytek nulami. Jakých součtů mohou nabývat řádky a sloupce a jak by mohly nasčítat  ?
?
Úloha 2a)+ skrytý text
Vyhovují jen 1 a 2.
Úloha 2b)+ skrytý text
Očísluj orgy 1 až 2n, pak počet úloh, pro které hlasovalo všech prvních x orgů (kde x<k) je  , což musím být celé číslo.
, což musím být celé číslo.
+ skrytý text
+ skrytý text
Zbytek dořeš Krummerovou větou.
Úloha 3a)+ skrytý text
Rozděl cifry a dvě skupiny a zkoumej rozdíl jejich součtů.
Úloha 3b)+ skrytý text
2 dny stačí.
+ skrytý text
+ skrytý text
Podle požadavků ptakopysků vytvoř cykly (p1,p2 až pk) a první den prohoď dvojice ptakopysků tak, aby ti cyklus rozpadl na dvojcykly.
+ skrytý text
+ skrytý text
pi prohoď s pk-i+1.
Úloha 4a)+ skrytý text
Sporem. Pak v 0 nabývá fce minima, z toho ukaž, že záporná čísla nabývají minima též. Srovnej s kladnými a ukaž sporem vhodným dosazením.
Úloha 4b)+ skrytý text
Existuje.
+ skrytý text
+ skrytý text
Vyřeš zvlášť pro {+-1,+-1/2} a zbylé body vyřeší "ořezaný kosočtverec".
Úloha 5a)+ skrytý text
Nejde.
+ skrytý text
+ skrytý text
Jaké budou nsd počtů kamenů v hromádkách po prvním kroku?
Úloha 5b)+ skrytý text
Přímky se musí protnout ve středu čtverce.
+ skrytý text
+ skrytý text
Kdyby ne, otoč podle středu každou přímku a spočítej obsahy úseků rozdělených těmito 4 přímkami.
Úloha 6a)+ skrytý text
Vměstnej do čtyřstěnu následující útvary 4 malé čtyřstěny a 4 trojúhelníky ze středních příček.
Úloha 6b)+ skrytý text
Zobraz například A podle středu N jako T a ukaž, že TEB leží na přímce.
+ skrytý text
+ skrytý text
Trojúhelníky TSE a CBE jsou shodné.
+ skrytý text
+ skrytý text
K tomu se hodí vědět jak daleko od roviny AMN leží body D,C,S.
Úloha 7a)+ skrytý text
Neexistuje
+ skrytý text
+ skrytý text
Jaké zbytky po dělení 4 může dávat hledaný součet?
Úloha 7b)+ skrytý text
n=9999
+ skrytý text
+ skrytý text
+ skrytý text
S(9999m)=36 pro m<10000
+ skrytý text
Jak k tomu dojít? Nejprve si všimni, že jde o nejmenší n, které splňuje S(n)=S(n1001).
+ skrytý text
+ skrytý text
Zkoumej zbytky po dělení 9.
+ skrytý textDále všimni si, že ciferný součet n s první jeho cifrou je roven první cifře.
Michal Töpfer | org | 8. 5. 2017 12:07:16
Ahoj,
chtěl bych se zeptat, jestli někdo nemáte tipy na nějaké lehké úlohy na Švrčkův bod. Koukal jsem do letošního seriálu i do knihovničky a tam je většina dost těžká (úlohy z IMO). Potřeboval bych úlohy tak pro prvák SŠ, takže možná něco z MO nebo minulých let PraSete, ale klidně i lehčí, pokud si na něco vzpomenete. Předem děkuji za rady.
chtěl bych se zeptat, jestli někdo nemáte tipy na nějaké lehké úlohy na Švrčkův bod. Koukal jsem do letošního seriálu i do knihovničky a tam je většina dost těžká (úlohy z IMO). Potřeboval bych úlohy tak pro prvák SŠ, takže možná něco z MO nebo minulých let PraSete, ale klidně i lehčí, pokud si na něco vzpomenete. Předem děkuji za rady.
Miroslav Olšák | org | 6. 5. 2017 11:56:35
Ahoj,
rozhodl jsem se vydat animovanou verzi své přednášky "Komplexní čísla geometricky". Enjoy!
http://atrey.karlin.mff.cuni.cz/~mirecek/Komp...
rozhodl jsem se vydat animovanou verzi své přednášky "Komplexní čísla geometricky". Enjoy!
http://atrey.karlin.mff.cuni.cz/~mirecek/Komp...
Marián Poppr | 17. 4. 2017 21:51:05
Ahoj,
Hinty k 3.jarní sérii spolu se závěrečnou seriálovou sérií jsou nýčko k nahlédnutí:
1. úloha+ skrytý text
2. úloha + skrytý text
3. úloha + skrytý text
1. úloha + skrytý text
2. úloha+ skrytý text
3. úloha + skrytý text
4. úloha + skrytý text
5. úloha + skrytý text
6. úloha + skrytý text
7. úloha + skrytý text
8. úloha + skrytý text
Hinty k 3.jarní sérii spolu se závěrečnou seriálovou sérií jsou nýčko k nahlédnutí:
1. úloha+ skrytý text
Všimni si, že L leží na AA´. V jakém vztahu je L a Gergonnův bod trojúhelníku A´B´C´? + skrytý text
Jsou totožné. Zbytek řeší záporná stejnolehlost z kamaráda Gergonnova bodu.
2. úloha + skrytý text
Jak vypadá feuerbachova křužnice trojúhelníku XYZ?+ skrytý text
Má poloviční poloměr oproti kružnici opsané a je pevně daná dvěma středy ze zadání. Mohla by být různá od  ?+ skrytý text
?+ skrytý text
Ne. Zobraz kružnici opsanou ve stejnolehlosti podle bodu X s vhodným koeficientem a použij ostroúhlou trojúhelníků.
3. úloha + skrytý text
OH prochází opsištěm A1B1C1+ skrytý text
Jak vypadá pedal triangle k bodu X v trojúhelníku A1B1C1?+ skrytý text
Nakonec použij druhou Fontenovu větu
1. úloha + skrytý text
chvilku si hraj
+ skrytý text
+ skrytý text
např 4066
2. úloha+ skrytý text
Neexistuje
+ skrytý text
+ skrytý text
Muselo by být tvaru pq^4 a zároveň dělitelné deseti
3. úloha + skrytý text
Kdy je číslo 700..0 -1 dělitelné 7?
4. úloha + skrytý text
n musí dělit rozdíl nějakých dvou čísel vybraných z n+1 nejmenších jedničkových čísel
+ skrytý text
+ skrytý text
dirichletův princip
5. úloha + skrytý text
Skus přičítání opakovat dokud nebude na tabuli číslo s větším počtem cifer.
6. úloha + skrytý text
50 jde a více ne
+ skrytý text
+ skrytý text
+ skrytý text
+ skrytý text
například prvních deset nech normálně a pak na střídačku vždy dalších deset buď nech jak jsou a nebo napiš pozpátku
+ skrytý text
spáruj čísla s čísly od 10 vyššími nebo menšími a použij dirichletův princip
+ skrytý text
jak se spárovaná čísla liší?
7. úloha + skrytý text
Řeš pro k>2 a všimni si, že n má stejný zbytek pod dělení k-1 jako jeho ciferný součet v soustavě o základu k.
+ skrytý text
+ skrytý text
Dále nahlédni, že k-kruté číslo nemůže mít více než 2k-2 cifer
+ skrytý text
+ skrytý text
Dirichletovým principem vyber 3 čísla se stejným zbytkem po dělení k-1 a zkoumej rozdíl největšího s nejmenším
8. úloha + skrytý text
+ skrytý text
+ skrytý text
N>=101
spoiler]Stačí ukázat pro 101. Pepa vysčítá desetinásobky čísel na lichých pozic a čísla na sudých pozicích, výsledek vymodulí 100 a zakryje čísla na výsledné a plus-první pozici
spoiler]Stačí ukázat pro 101. Pepa vysčítá desetinásobky čísel na lichých pozic a čísla na sudých pozicích, výsledek vymodulí 100 a zakryje čísla na výsledné a plus-první pozici
+ skrytý text
Pro N<100 srovnej počet možných stavů, které může Pepa vytvořit s počtem možných čísel
+ skrytý text a
a 
+ skrytý text
Štěpán Šimsa | org | 25. 3. 2017 00:45:53
Ahoj,
kdo by chtěl na poslední chvíli potrénovat před celostátkem MO, může si udělat k tomu určený TRiKS http://iksko.org/triks/current.php.
kdo by chtěl na poslední chvíli potrénovat před celostátkem MO, může si udělat k tomu určený TRiKS http://iksko.org/triks/current.php.
Marián Poppr | 7. 3. 2017 20:24:17
Hle,
nové Hinty,
zde.
1.úloha + skrytý text
2.úloha + skrytý text
3.úloha + skrytý text
4.úloha + skrytý text
5.úloha + skrytý text
6.úloha + skrytý text
7.úloha + skrytý text
8.úloha + skrytý text
nové Hinty,
zde.
1.úloha + skrytý text
2.úloha + skrytý text
posuň vrchol jehlanu nad jeden z vrcholů podstavy
3.úloha + skrytý text
Z vrcholů krychle vyber ty, co tvoří pravidelný čtyřstěn a promítni ho na jednu stanu krychle.
4.úloha + skrytý text
Vezměme rovinu danou středem slunce a libovolnými dvěma planetami. Tato rovina protne slunce na rovníku, kolik pak planet vidíme z jednotlivých pólů?
5.úloha + skrytý text
Pepa propadne hrdlem+ skrytý text
srovnej objem, jaký největší mohou zabírat jehlany, s objemem hranolu
6.úloha + skrytý text
body D leží na kouli s průměrem AB+ skrytý text
zbytek obstará stereografická projekce
7.úloha + skrytý text
Množiny bodů dotyků z A,B,C,D se sférou tvoří vně se dotýkající kružnice kA,kB,kC,kD. Zvolme si například bod A1, jakožto bod dotyku kA a kB. Jak se zobrazí ve stereografické projekci na rovinu kružnice kA, kB, kC, kD, když A1 je severní pól?+ skrytý text
k´A a k´B budou rovnoběžky a k´C a k´D jsou kružnice navzájem se vně dotýkající, k´C se dotýká k´B a k´D se dotýká k´A.+ skrytý text
Tyto tři body dotyku leží ze stejnolehlosti na přímce, což řeší úlohu
8.úloha + skrytý text
Zvolme si vrchol A1 u našeho mnohostěnu M a nafoukněme M ve stejnolehlosti se středem v A1 a koeficientem 2. Tím získáme mnohoúhelník M´.+ skrytý text
Jak velký je objem M vzhledem k M´+ skrytý text
8 krát menší
+ skrytý textS každým bodem z M´ je v M jeho polovina+ skrytý text
Tedy objem M´je patrně menší než objem všech devíti zformovaných mnohoúhelníků
Marián Poppr | 20. 2. 2017 20:33:31
Ahoj,
s lehkým zpozděním, ale přece, světlo světa spatřily nové Hinty a Nápovědy k 1. jarní a 2. seriálové sérii. Nechť milý čtenář shlédne níže.
1. úloha + skrytý text
2. úloha + skrytý text
3. úloha + skrytý text
4. úloha + skrytý text
5. úloha + skrytý text
6. úloha + skrytý text
7. úloha + skrytý text
8. úloha + skrytý text
1. úloha + skrytý text
2. úloha + skrytý text
3. úloha + skrytý text
s lehkým zpozděním, ale přece, světlo světa spatřily nové Hinty a Nápovědy k 1. jarní a 2. seriálové sérii. Nechť milý čtenář shlédne níže.
1. úloha + skrytý text
Kdy sní mravenečník jiný počet mravenců než předešlý den?
2. úloha + skrytý text
Ne
3. úloha + skrytý text
Kolik vede cest z každého města?+ skrytý text
celkem je 5 měst
4. úloha + skrytý text
Seřaď sýry od nejlehčího sýra po nejtěžší a všechny liché (bez nejtěžšího sýra). Poté dej liché do jedné a všechny sudé do druhé skupiny. Všimni si, že rozdíl těchto skupin musí být lehčí než poslední sýr, což řeší úlohu
5. úloha + skrytý text
Kdyby v každé skupině existovalo nějaké číslo s konečným počtem násobků, tak kolikrát by byl zastoupen součin násobků všech těchto čísel v daných skupinách?
6. úloha + skrytý text
MaM :)
7. úloha + skrytý text
Použij mocnost bodu ke kružnici pro každý z vrcholů n-úhelníku. Co tím získáme pro přečuhující úseky tras ptakopysků?
8. úloha + skrytý text
Snaž se najít dokonalé párování v bipartijním grafu s partitami podle obou návrhů. Hranu mezi nimi povedeš, pokud mají odpovídající okresy nenulový průnik+ skrytý text
Použij Hallovu větu
1. úloha + skrytý text
Daná opsiště leží na ose BP+ skrytý text
Nechť N je antišvrk pro bod B, všimni si, že osy stran ICB,IAB a BN procházejí odpovídajícími opsištěmi, tedy stačilo by ukázat, že osa BN půlí pás mezi ICB a IAB+ skrytý text
stejnolehlost se středem v B a koeficientem 2
2. úloha + skrytý text
PQ a RS se protínají na AB v bodě T+ skrytý text
Simpsonova přímka
+ skrytý textpětiúhelníky QYSBM a APYRS leží na kružnicích
+ skrytý text
+ skrytý text
+ skrytý text
Pravé úhly
+ skrytý text
A nakonec trochu úhlení
3. úloha + skrytý text
P a V jsou kamarádi
+ skrytý text
+ skrytý text
+ skrytý text
six feet tvorem
+ skrytý text
Zbytek troška hraní si s úhly kamarádů





