Zboňk | org | 12. 7. 2020 17:52:47
Řešení 2:
+ skrytý text
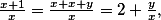 takže pokud označíme
takže pokud označíme 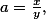 , tak díky AG a Cauchymu platí:
, tak díky AG a Cauchymu platí:
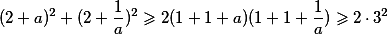 a jsme doma.
a jsme doma.
3. V trojúhelníku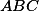 s opsištěm
s opsištěm 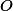 a těžištěm
a těžištěm 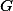 platí
platí 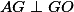 . Označme
. Označme 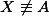 druhý průsečík
druhý průsečík 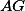 s kružnicí
s kružnicí 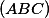 a mějme
a mějme 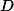 průsečík přímek
průsečík přímek 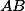 a
a 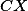 ,
, 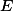 průsečík
průsečík 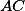 a
a 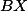 . Ukaž, že opsiště
. Ukaž, že opsiště 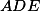 leží na
leží na 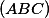 .
.
+ skrytý text
3. V trojúhelníku
Huu Quy Nguyen | 12. 7. 2020 15:03:08
Řešení:
+ skrytý text
Dokážeme matematickou indukcí :)
Pro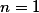 tvrzení zřejmě platí.
tvrzení zřejmě platí.
Předpokládejme, že tvrzení platí pro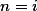 .
.
Pak z indukčního předpokladu platí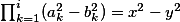 pro celá
pro celá 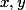 .
.
Nyní pro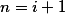 platí
platí 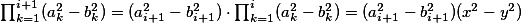
Jenže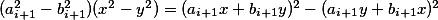 , což je rozdíl dvou čtverců, čímž jsme hotovi.
, což je rozdíl dvou čtverců, čímž jsme hotovi.
2. Pro kladná reálná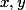 platí
platí 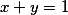 . Dokaž, že platí
. Dokaž, že platí 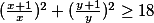
+ skrytý text
Dokážeme matematickou indukcí :)
Pro
Předpokládejme, že tvrzení platí pro
Pak z indukčního předpokladu platí
Nyní pro
Jenže
2. Pro kladná reálná
Fíla | 11. 7. 2020 22:51:48
Ahoj,
jelikož je ti určitě smutno, že už tento rok skončily prasečí série, nechceš zakrnět, a proto by sis rád vyřešil nějaké úložky navíc. Proto bychom rádi obnovili prasečí maraton.
Pravidla jsou následující. Vždy když vyřešíš nejnovější úlohu, napíšeš její řešení a hned zadáš další. Nějací orgové se určitě připojí také, když se budou moc nudit ;) (prosím abyste řešení dávali formou skrytého textu, aby si ji i ostatní mohli vyřešit a hned neviděli řešení).
1.
Dokažte, že pro libovolná přirozená čísla ,
, 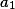 ,
, 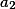 ,
,  ,
, 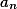 ,
,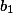 ,
, 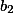 ,
,  ,
, 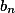 je možné zapsat součin
je možné zapsat součin 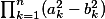 jako rozdíl dvou čtverců (celých čísel).
jako rozdíl dvou čtverců (celých čísel).
jelikož je ti určitě smutno, že už tento rok skončily prasečí série, nechceš zakrnět, a proto by sis rád vyřešil nějaké úložky navíc. Proto bychom rádi obnovili prasečí maraton.
Pravidla jsou následující. Vždy když vyřešíš nejnovější úlohu, napíšeš její řešení a hned zadáš další. Nějací orgové se určitě připojí také, když se budou moc nudit ;) (prosím abyste řešení dávali formou skrytého textu, aby si ji i ostatní mohli vyřešit a hned neviděli řešení).
1.
Dokažte, že pro libovolná přirozená čísla
Olin | org | 8. 6. 2020 01:40:58
Na krajská kola MO B+C už se dá i registrovat:
https://mo.mff.cuni.cz/bc/
https://mo.mff.cuni.cz/bc/
Miroslav Olšák | org | 6. 6. 2020 15:30:51
Ahoj, po delší době jsem zase udělal animované video inspirované PraSečí přednáškou, tentokrát o Burnsideově lemmatu -- jak počítat se zanedbáváním symetrií:
http://www.olsak.net/mirek/manim/burnside_cz.mp4
Enjoy!
http://www.olsak.net/mirek/manim/burnside_cz.mp4
Enjoy!
Josef Tkadlec | 4. 6. 2020 00:18:43
Dve novinky ze sveta matematicke olympiady:
1) Na webu ceske MO (http://www.matematickaolympiada.cz/ ) se objevilo info o nahradnich internetovych soutezich za krajska kola B+C (20.6.) a celostatko A (29.+30.6.).
2) IMO 2020 (https://imo2020.ru/ ) je ted naplanovane jako virtualni, v datech 21.+22.9.
1) Na webu ceske MO (http://www.matematickaolympiada.cz/ ) se objevilo info o nahradnich internetovych soutezich za krajska kola B+C (20.6.) a celostatko A (29.+30.6.).
2) IMO 2020 (https://imo2020.ru/ ) je ted naplanovane jako virtualni, v datech 21.+22.9.
Dominik Stejskal | 18. 5. 2020 19:38:40
I k poslední letošní sérii úloh patří série hintů. No a další zase na podzim. :)
Úloha 1.
(a) + skrytý text
(b) + skrytý text
Úloha 2.
(a) + skrytý text
(b) + skrytý text
Úloha 3.
(a) + skrytý text
(b) + skrytý text
Úloha 4.
(a) + skrytý text
(b) + skrytý text
Úloha 5.
(a) + skrytý text
(b) + skrytý text
Úloha 6.
(a) + skrytý text
(b) + skrytý text
Úloha 7.
(a) + skrytý text
(b) + skrytý text
Úloha 1.
(a) + skrytý text
Neexistuje. Hledej monovarianty. + skrytý text
Maximální počet brambor na jednom talíři se nezvětšuje, zato celkový počet ano.
(b) + skrytý text
Ukaž, že z konstrukce pro n+1 vznikne odebráním učitele s n+1 klobáskami konstrukce pro n. + skrytý text
Pro sudá n je až na symetrii jen jedna možnost, pro lichá n > 3 jsou dvě.
Úloha 2.
(a) + skrytý text
Ano, může. Postupuj indukcí. + skrytý text
Zvětši si nějaký člen tak, aby byl alespoň o 2 větší než libovolný jiný.
(b) + skrytý text
Neexistuje. Jaké počáteční hodnoty by členy musely mít? + skrytý text
Nechť BÚNO začínáme s nulami a jedničkami. Je možné poslední nulu zvětšit o 2?
Úloha 3.
(a) + skrytý text
Použij šachovnicové obarvení. + skrytý text
Rozdíl součtu čísel na černých a bílých políčkách se nemění.
(b) + skrytý text
Zkus ze dvou pokrytí n (nebo n-1) políček zkonstruovat pokrytí 2n+1 políček.
Úloha 4.
(a) + skrytý text
Pomocí věty o obvodových úhlech ukaž, že úhly DBC a DCB se oba rovnají polovině úhlu ABC.
(b) + skrytý text
Dokresli si střed PS a najdi podobné trojúhelníky.
Úloha 5.
(a) + skrytý text
Použij hrubé horní odhady na jednotlivé ciferné součty. + skrytý text
s(n) dává stejný zbytek po dělení 9 jako n.
(b) + skrytý text
Ukaž, že a,b,c < 1. + skrytý text
(a+1)(b+1)(c+1) - 4 = (a-1)(b-1)(c-1).
Úloha 6.
(a) + skrytý text
Na jedničku je možné se dostat pouze z k-ciferného čísla tvaru 11...1. Ukaž, že takové číslo je pro k > 1 dělitelné prvočíslem větším než 7, a tedy se na něj nedá dostat. + skrytý text
Pokud 3 | k, tak 37 | 11...1. Ukaž, že jinak není 11...1 dělitelné žádným z prvočísel 2, 3, 5, 7.
(b) + skrytý text
Může se mu to podařit. Zaplňuj rovinu po spirále. Při zaplňování bodu by bylo ideální, kdyby Martin mohl použít Čínskou zbytkovou větu a najít tak číslo, které lze do mřížky přidat. To ale není možné udělat přímo. + skrytý text
Martin může Čínskou zbytkovou větu použít na "nejlepší možnou" množinu čtverců. Ukaž, že je úloha nastavena tak, aby to vyšlo. + skrytý text
Nechť největší čtverec obsahující přidávaný bod má rozměr m x m. Použij Čínskou zbytkovou větu tak, aby pro každé prvočíslo p <= m byl součet čísel ve čtverci o rozměrech p^floor(log_p(m)) x p^floor(log_p(m)) dělitelný p^floor(log_p(m)). + skrytý text
Vezmi si libovolný čtverec s x s obsahující přidávaný bod a dokaž, že součet čísel v něm je dělitelný libovolným prvočíslem ve stejné mocnině jako s. Použij, co víš, a šikovně dláždi větší čtverce menšími. + skrytý text
Ukaž, že do "rohů" spirály je možno umístit libovolné číslo. Ukaž, že už tak dokážeš napsat do roviny každé přirozené číslo jednou.
Úloha 7.
(a) + skrytý text
Pokud je jeden čtverec prázdný, jsou dámy jenom ve dvou čtvercích. + skrytý text
Pokryj je diagonálami.
(b) + skrytý text
Poskládej nejdřív kartičky do balíčků se součtem L*n, kde 1 <= L <= n-1. + skrytý text
Potom takový balíček ber jako jednu kartu s hodnotou L a použij indukční předpoklad.
Pavel Hudec | 9. 5. 2020 18:03:51
Ahoj,
skupinka úspěšných amerických olympioniků rozjíždí projekt online přednášek zdarma nazvaný Math Divulged. Přednášky začínají vždy ve 22:00 našeho času a je možné si je pouštět i zpětně. Program vypadá následovně:
Pondělí - úvod do soutěží, nepříliš obtížná série přednášek, můžete je zkusit, pokud si tolik nevěříte, případně je můžete doporučit pikomaťákům nebo svým mladším sourozencům.
Středa - olympiádní přednášky podobné jako na PraSečích sousech.
Pátek - semináře jdoucí více do šířky zaměřené na různá témata spojená s matematikou (VŠ matematika, různé vědní obory, biologické modely aj.)
Sobota - jiný pohled na témata běžného středoškolského učiva s důrazem na "proč" namísto biflování.
Kompletní informace a odkaz na videopřednášky pak najdete na https://sites.google.com/view/mathdivulged/.
skupinka úspěšných amerických olympioniků rozjíždí projekt online přednášek zdarma nazvaný Math Divulged. Přednášky začínají vždy ve 22:00 našeho času a je možné si je pouštět i zpětně. Program vypadá následovně:
Pondělí - úvod do soutěží, nepříliš obtížná série přednášek, můžete je zkusit, pokud si tolik nevěříte, případně je můžete doporučit pikomaťákům nebo svým mladším sourozencům.
Středa - olympiádní přednášky podobné jako na PraSečích sousech.
Pátek - semináře jdoucí více do šířky zaměřené na různá témata spojená s matematikou (VŠ matematika, různé vědní obory, biologické modely aj.)
Sobota - jiný pohled na témata běžného středoškolského učiva s důrazem na "proč" namísto biflování.
Kompletní informace a odkaz na videopřednášky pak najdete na https://sites.google.com/view/mathdivulged/.
Lenka Kopfová | 25. 4. 2020 14:45:22
Ahoj,
taky Ti chybí Náboj? Možnost jet na jarní soustředění a pořádně si tam zasoutěžit?
Tak máme příležitost právě pro Tebe!
Příští pátek se totiž uskuteční Mecz Online. ⚔️
Co je to Mecz?
Je týmová soutěž, kde každý tým dostane 4-8 úloh a jejich cílem je úlohy v časovém limitu vyřešit. Úlohy jsou během soutěže vysvětlovány online organizátorům. Více detailů upřesníme podle počtu účastníků.
Povolené pomůcky:
Viz standardní pravidla MO. Tedy jedině psací a rýsovací potřeby, žádné mobily, telefony, kalkulačky, wolframy, geogebry a jiné prevíty.
Týmy budou po 1-5 lidech. Můžete se na týmu domluvit sami, ale nebojte se, pokud nikoho neznáte, nebo to si nejste jistí, koho vybrat, napiště své jméno na prázdný řádek tabulky a v poznámky napište "Hledám Tým!" nebo se dohodněte s někým, kdo už tým hledá ;)
https://docs.google.com/spreadsheets/d/1BlYzb...
Kdy?
1.5.2020 (Pátek) v 16.00.
Délka?
Tři hodiny.
Kde?
Váš tým může může komunikovat využitím jakéhokoli komunikačního přistroje (pokud jste v jedné domácnost, nemusíte si volat).
Doporučené:
https://hangouts.google.com/, https://www.skype.com/, Messenger, https://meet.jit.si/
Další užitečné pomůcky:
Online whiteboard https://awwapp.com/
Přičemž samotná komunikace s orgy bude probíhat pravděpodobně přes https://meet.jit.si/.
Všechny podrobnosti upřesníme během týdne podle zájmu.
taky Ti chybí Náboj? Možnost jet na jarní soustředění a pořádně si tam zasoutěžit?
Tak máme příležitost právě pro Tebe!
Příští pátek se totiž uskuteční Mecz Online. ⚔️
Co je to Mecz?
Je týmová soutěž, kde každý tým dostane 4-8 úloh a jejich cílem je úlohy v časovém limitu vyřešit. Úlohy jsou během soutěže vysvětlovány online organizátorům. Více detailů upřesníme podle počtu účastníků.
Povolené pomůcky:
Viz standardní pravidla MO. Tedy jedině psací a rýsovací potřeby, žádné mobily, telefony, kalkulačky, wolframy, geogebry a jiné prevíty.
Týmy budou po 1-5 lidech. Můžete se na týmu domluvit sami, ale nebojte se, pokud nikoho neznáte, nebo to si nejste jistí, koho vybrat, napiště své jméno na prázdný řádek tabulky a v poznámky napište "Hledám Tým!" nebo se dohodněte s někým, kdo už tým hledá ;)
https://docs.google.com/spreadsheets/d/1BlYzb...
Kdy?
1.5.2020 (Pátek) v 16.00.
Délka?
Tři hodiny.
Kde?
Váš tým může může komunikovat využitím jakéhokoli komunikačního přistroje (pokud jste v jedné domácnost, nemusíte si volat).
Doporučené:
https://hangouts.google.com/, https://www.skype.com/, Messenger, https://meet.jit.si/
Další užitečné pomůcky:
Online whiteboard https://awwapp.com/
Přičemž samotná komunikace s orgy bude probíhat pravděpodobně přes https://meet.jit.si/.
Všechny podrobnosti upřesníme během týdne podle zájmu.
Michaela Hubatová | 17. 4. 2020 03:49:06
Ahoj všem a hurá!
Následující týmová matematická soutěž proběhne navzdory COVID-19!
Mezinárodní online týmová matematická soutěž Purple Comet! Math Meet se letos uskuteční od 21. do 30. dubna. Je určena pro až šestičlenné týmy. Není třeba se fyzicky scházet, můžete při soutěži spolupracovat například prostřednictvím oblíbeného chatu či videohovoru. Potřebovat budete tedy připojení k internetu a dospělého supervisora, který Váš tým zaregistruje. Registrace již probíhá a bude možná až do konce soutěžního období. Zadání bude k dispozici i v češtině (jsem autorkou překladů).
Stručné informace o soutěži v čestině naleznete na https://purple-comet-cesky.webnode.cz/.
Úplné informace naleznete v angličtině na http:// https://purplecomet.org/
Následující týmová matematická soutěž proběhne navzdory COVID-19!
Mezinárodní online týmová matematická soutěž Purple Comet! Math Meet se letos uskuteční od 21. do 30. dubna. Je určena pro až šestičlenné týmy. Není třeba se fyzicky scházet, můžete při soutěži spolupracovat například prostřednictvím oblíbeného chatu či videohovoru. Potřebovat budete tedy připojení k internetu a dospělého supervisora, který Váš tým zaregistruje. Registrace již probíhá a bude možná až do konce soutěžního období. Zadání bude k dispozici i v češtině (jsem autorkou překladů).
Stručné informace o soutěži v čestině naleznete na https://purple-comet-cesky.webnode.cz/.
Úplné informace naleznete v angličtině na http:// https://purplecomet.org/
Lenka Kopfová | 10. 4. 2020 23:59:58
Ahoj,
Švýcaři se rozhodli být aktivní a vytvořili něco jako trochu víc fancy mezinárodní TRiKS. Nemám moc odhad na obtížnost, ale jsou tam dvě kategorie (zkušení/nováčci) a člověk určitě nic nezkazí, když zkusí něco nového :-) Rozhodně bych se toho nebála :)
Odkaz na stránky tady https://facebook.com/events/s/global-quaranti.... K soutěžení je potřeba vyplnit nějaký google form (odkaz na stránkách). A pokud ještě stále váháš, tak neváhej, páč registrace je prý do neděle.
Veselé Velikonoce a hodně čokoládových vajíček,
Lenka
Švýcaři se rozhodli být aktivní a vytvořili něco jako trochu víc fancy mezinárodní TRiKS. Nemám moc odhad na obtížnost, ale jsou tam dvě kategorie (zkušení/nováčci) a člověk určitě nic nezkazí, když zkusí něco nového :-) Rozhodně bych se toho nebála :)
Odkaz na stránky tady https://facebook.com/events/s/global-quaranti.... K soutěžení je potřeba vyplnit nějaký google form (odkaz na stránkách). A pokud ještě stále váháš, tak neváhej, páč registrace je prý do neděle.
Veselé Velikonoce a hodně čokoládových vajíček,
Lenka
Dominik Stejskal | 10. 4. 2020 01:30:06
Blížíme se ke konci roku a přichází předposlední, pro velký úspěch dvojitá várka hintů!
3. jarní série:
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
3. seriálová série:
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
3. jarní série:
Úloha 1. + skrytý text
2025 = 45^2.
Úloha 2. + skrytý text
Stačí 1010 vteřin.
Úloha 3. + skrytý text
Vyber si tým, který porazil aspoň 4 týmy. Poté uvažuj pouze tyto týmy a opakuj.
Úloha 4. + skrytý text
Nechť je R průsečík ramen BC, DA. V jakém poměru dělí body, kde míče přešly přes brankovou čáru, úsečku RA?
Úloha 5. + skrytý text
Uvaž polynom P(t+1)-P(t)
.Úloha 6. + skrytý text
Zjisti, co v tomto kontextu znamená výraz (abc)/(ab + bc + ca). Díky tomu najdi výraz, který se v průběhu procesu nemění. + skrytý text
Dokaž, že součet převrácených hodnot čísel na tabuli se nemění.
Úloha 7. + skrytý text
Žabák může projít všechny kameny tak, aby pouze v jednom skoku vydělal jednu korunu. + skrytý text
Navrhni konstrukci a u ní urči počet skoků délky 2^k. + skrytý text
Spočítej jaký může být počet skoků délky větší než 2^k pro fixní k. + skrytý text
Ukaž, že nalezený počet skoků dané délky je nejlepší možný.
Úloha 8. + skrytý text
V pravoúhlém trojúhelníku je √2-násobek délky přepony větší nebo roven součtu délek odvěsen. + skrytý text
Rozděl si trasu na úseky mezi body kde Filip mění směr jízdy vzhledem ke spádnici.
3. seriálová série:
Úloha 1. + skrytý text
Dokresli střed oblouku BC.
Úloha 2. + skrytý text
Dokresli body naproti bodům B a C.
Úloha 3. + skrytý text
Najdi DDIT, kterým dostaneš dvojice bodů na kružnici Ω (E,F), (A,M), (B,C) v jedné involuci.
Pavel Hudec | 20. 3. 2020 20:18:52
Jsi smutný/á, že příští týden nebude celostátko? Máš teď hromadu času, tápeš a nevíš, co s ním? Chceš se dostat na přespříští IMO (a případně ho vyhrát)?
Pokud jsi alespoň na 0 otázek odpověděl/a ano a jsi středoškolák, pak je tu pro tebe seminář iKS, taková verze PraSátka pro zkušenější řešitele. Právě začíná nový ročník, zadání první série najdeš na http://iksko.org. I jedna vyřešená úloha už může znamenat slušné umístění!
Zároveň je pro vás připraven na iKSkových stránkách celostátkový TRiKS, díky němuž celostátko můžete zkusit nanečisto a přitom potrénovat.
Pokud jsi alespoň na 0 otázek odpověděl/a ano a jsi středoškolák, pak je tu pro tebe seminář iKS, taková verze PraSátka pro zkušenější řešitele. Právě začíná nový ročník, zadání první série najdeš na http://iksko.org. I jedna vyřešená úloha už může znamenat slušné umístění!
Zároveň je pro vás připraven na iKSkových stránkách celostátkový TRiKS, díky němuž celostátko můžete zkusit nanečisto a přitom potrénovat.
Dominik Stejskal | 6. 3. 2020 00:19:30
Tak jak to v té 2. jarní sérii mělo vyjít? Hinty napoví!
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Jestliže nějaké k není dělitelem n, tak ani 2k není dělitelem n.
Úloha 2. + skrytý text
Jaká prvočísla se musí objevit v rozkladu? Čím musí být dělitelné exponenty?
Úloha 3. + skrytý text
Jedno vyhovující n se dá přímo vyjádřit pomocí a a b. + skrytý text
n = ab.
Úloha 4. + skrytý text
NSD(n,kn) = ? + skrytý text
A co třeba NSD(a_n, a_(a_n))?
Úloha 5. + skrytý text
Začni zkoumáním parity. + skrytý text
Dále si všimni monotonie vhodné funkce.
Úloha 6. + skrytý text
Uvědom si, že stačí, aby bylo každé n nesoudělné s každým P(...(P(n)...). + skrytý text
Jednička je se vším nesoudělná. + skrytý text
Zajisti, aby P(n) ≡ P(1) ≡ 1 (mod n). + skrytý text
P(n) = n^2020 - n + 1.
Úloha 7. + skrytý text
Smazáním jednotlivých čísel dostaneš jako součty n po sobě jdoucích čísel. + skrytý text
Každé napsané číslo může dělit pouze jeden součet. + skrytý text
Najdi číslo, jehož smazáním vznikne součet dělitelný dvěma napsanými čísly. Ukaž, že to už stačí.
Úloha 8. + skrytý text
Není to pravda. + skrytý text
Najdi vhodný polynom a zkoumej kvadratické zbytky modulo p. + skrytý text
Rozlož x^8 - 16 na součin.
Josef Tkadlec | 16. 2. 2020 22:25:59
Vedeli jste, ze na https://h.evanchen.cc/hydrogen/active/ is dnes a v pondeli muzete online zkusit letosni HMMT (Harvard-MIT Math Tournament)? Tri ruzne testy (algebra+teorie cisel, geometrie. kombinatorika), v kazdem 10 uloh na ciselny vysledek na 50 minut. Idealni trenink na Naboj pro borce :). (Ulohy z lonska na https://www.hmmt.co/www/archive/222.)
Dominik Stejskal | 6. 2. 2020 00:46:32
Pokud pořád nevíš, jak se vypořádat s tou zapeklitou úlohou, zkrať si čekání a mrkni na další hinty!
1. jarní série:
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
2. seriálová série:
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
1. jarní série:
Úloha 1. + skrytý text
Prostřední čtyři políčka mají všechny čtverce 3x3 společné.
Úloha 2. + skrytý text
Použij Pythagorovu větu.
Úloha 3. + skrytý text
Zkus umocnit 38. Dále použij zbytky po dělení 16.
Úloha 4. + skrytý text
Body A', B', C', D' leží na úhlopříčkách.
Úloha 5. + skrytý text
Rozmysli si, že a_{2n} = a_n pro n sudé a a_{2n} = a_n + 1 pro n liché. + skrytý text
Z předchozího odvoď, že libovolná hodnota, která se v posloupnosti vyskytne, se v ní znovu zopakuje, a že posloupnost nabude libovolně velké hodnoty.
Úloha 6. + skrytý text
Uvažuj střetnutí 2 orgů jako hranu v (úplném) grafu. Počet hran musí být dělitelný počtem hran úplného bipartitního grafu K_{4,4}. + skrytý text
Dále počet 'sousedů' každého orga musí být dělitelný čtyřmi. + skrytý text
Vyjde 32k + 1.
Úloha 7. + skrytý text
Podívej se na průsečíky os úhlů s protějšími stranami v jednotlivých trojúhelnících - stěnách. + skrytý text
Nechť je v trojúhelníku ABC bod P průsečíkem osy úhlu BAC a strany BC. Pak |BP| / |CP| = |BA| / |CA|.
Úloha 8. + skrytý text
Využij symetrii výrazu xy - zt vzhledem k proměnným x, y.
2. seriálová série:
Úloha 1. + skrytý text
Zinvertuj se středem v X. + skrytý text
Vyúhli, že výsledný čtyřúhelník bude podobný s původním.
Úloha 2. + skrytý text
Zinvertuj podle Z. + skrytý text
Z kolmých kružnic se stanou kolmé přímky.
Úloha 3. + skrytý text
Dokaž, že úhly PXQ a PYQ jsou pravé. + skrytý text
Zapomeň na Y a zdualizuj podle X. Kružnice nad průměrem převeď na pravé úhly.
Dominik Stejskal | 8. 1. 2020 20:50:58
Nový rok, nové hinty ke 4. podzimní sérii!
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Zvol jako průsečíky vrcholy rovnostranného trojúhelníku, jeho středy stran a jeho střed.
Úloha 2. + skrytý text
Označ si jeden úhel, všimni si dvou rovnoramenných trojúhelníků a počítej.
Úloha 3. + skrytý text
Uvaž trojúhelník ze středů původních tří kružnic, všimni si, že je rovnoramenný a počítej. Bude se hodit Pythagorova věta.
Úloha 4. + skrytý text
Ukaž, že P, Q, R, S jsou středy stran čtyřúhelníku ABCD.
Úloha 5. + skrytý text
Spoj si body P, T, C se středy kružnic a podívej se na úhly mezi přímkami.
Úloha 6. + skrytý text
Rozmysli si, kdy vznikne součet n^2. + skrytý text
Obarvi si body označené čísly větší než n modře a menší než m červeně a rozmysli si, že můžeš jakkoliv spojit různobarevné body.
Úloha 7. + skrytý text
Dokresli bod Y takový, že BHAY je obdélník. Tento bod leží také na kružnici opsané CDHE.
Úloha 8. + skrytý text
Všimni si, že šestiúhelník z definovaných středů úseček má protější strany rovnoběžné. Poté ukaž, že průsečík dvou z těchto kružnic leží i na té třetí.
Danil Koževnikov | 2. 1. 2020 16:26:39
Pojďte potrénovat před krajským kolem kategorie A (to je 14. ledna) ve speciálním TriKSu: http://iksko.org/triks/current.php! Soutěž trvá až do krajského kola a začíná dnes o půlnoci, takže můžete být první, kdo vyřeší všechny úlohy :-) Na řešení čtyř úloh jsou čtyři hodiny.
Michal Buran | 9. 12. 2019 12:26:51
Orgové, jeďte orgovat na PROMYS. Účastníci, jeďte se zúčastnit.
PROMYS Europe 2020 – Advance Notification
PROMYS Europe is designed to encourage mathematically ambitious students who are at least 16 to explore the creative world of mathematics. Participants tackle fundamental mathematical questions within a richly stimulating and supportive community of fellow first-year students, returning students, undergraduate counsellors, research mentors, faculty, and visiting mathematicians.
Please be advised that:
Applications for Counsellors and Returning Students will open on 3 January 2020
Applications for First Year Students will open on 13 January 2020
For more information please visit our website http://www.promys-europe.org.
PROMYS Europe 2020 – Advance Notification
PROMYS Europe is designed to encourage mathematically ambitious students who are at least 16 to explore the creative world of mathematics. Participants tackle fundamental mathematical questions within a richly stimulating and supportive community of fellow first-year students, returning students, undergraduate counsellors, research mentors, faculty, and visiting mathematicians.
Please be advised that:
Applications for Counsellors and Returning Students will open on 3 January 2020
Applications for First Year Students will open on 13 January 2020
For more information please visit our website http://www.promys-europe.org.
Dominik Stejskal | 4. 12. 2019 20:56:52
Ani tentokrát nebudou po uplynutých termínech odeslání chybět hinty.
3. Podzimní série:
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
1. seriálová série:
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
3. Podzimní série:
Úloha 1. + skrytý text
Do tří políček si napiš neznámé a vyjadřuj.
Úloha 2. + skrytý text
Kolik je prvočísel mezi 40 a 81?
Úloha 3. + skrytý text
Podívej se na vrstvu 8x8. Umíš ji celou zaplnit?
Úloha 4. + skrytý text
Cena každé dlaždičky je rovna polovině počtu čtverečků plus jedna.
Úloha 5. + skrytý text
Rozděl tabulku na několik čtverečků, L-triomin a pár přebývajících políček.
Úloha 6. + skrytý text
Podmínku pro řádky interpretuj jako dosazení do polynomu.
Úloha 7. + skrytý text
Obarvování si představuj jako čísla 0, 1, 2. Postupuj od rohu a ve chvíli, kdy se barva musí měnit, měň algoritmus dle parity vzdálenosti od začátku.
Úloha 8. + skrytý text
Rozeber zvlášť liché a sudé. Obarvi vrcholy černě a bíle a rozmysli si, jak často musíš změnit barvu.
1. seriálová série:
Úloha 1. + skrytý text
Afinním zobrazením udělej trojúhelník rovnostranný.
Úloha 2. + skrytý text
Pomocí kolineace zachovej kružnici vepsanou a zobraz XY na nevlastní. + skrytý text
Vznikne kosočtverec.
Úloha 3. + skrytý text
Převeď úhlovou podmínku pomocí "dvě ze tří" na harmonickou čtveřici. + skrytý text
Zobraz ABCD na čtverec. Harmonická čtveřice se zachová.




