Kenny | 10. 5. 2011 19:44:54
A já hned přidám jednu lehkou úlohu z celkem aktuální soutěže! Takže, řešitelé, pokud ji nevyřešíte do dnešní půlnoci (sem na chat), jste pěkné lamy! Tak dotoho!
Kladná reálná čísla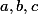 splňují
splňují 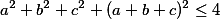
Dokažte, že
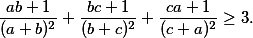
A přidám ještě drobnou motivaci. S Pavlem se chystáme vydat náš loňský seriál jako samostatnou brožurku, tak můžeme vítězi slíbit, že dostane podepsané vydání :P
Kladná reálná čísla
Dokažte, že
A přidám ještě drobnou motivaci. S Pavlem se chystáme vydat náš loňský seriál jako samostatnou brožurku, tak můžeme vítězi slíbit, že dostane podepsané vydání :P
Štěpán | 10. 5. 2011 19:01:46
to je v podstatě spíš řešení než hint, ne? :D
Miroslav Olšák | 10. 5. 2011 00:55:52
Velká cena 4b) byla nepokořena. Nechce-li se vám čekat na vzoráky, můžete ji zkusit vyřešit s hintem: Ramseyova věta říká, že pokud obarvíme hrany nekonečného úplněho grafu konečně mnoha barvami, pak bude existovat nekonečná jednobarevná klika (úplný podgraf).
Pepa T. | 10. 5. 2011 00:54:20
Ahojte,
Tam ta da dá, tímto uzavírám soutěž o velké ceny. Výsledky jsou na http://mks.mff.cuni.cz/velkeceny.php. Pokud se vám nechce čekat na vzorová řešení, nebo chcete k některým úlohám hinty, tažte se :). A komu se nezadařilo, nemusí plakat, brzy si zase dáme nějakou tlustou úlohu :).
Tam ta da dá, tímto uzavírám soutěž o velké ceny. Výsledky jsou na http://mks.mff.cuni.cz/velkeceny.php. Pokud se vám nechce čekat na vzorová řešení, nebo chcete k některým úlohám hinty, tažte se :). A komu se nezadařilo, nemusí plakat, brzy si zase dáme nějakou tlustou úlohu :).
Kenny | 3. 5. 2011 15:57:42
Roznásobíme a jako obvykle sečteme cyklické AG nerovnosti.
Konkrétně
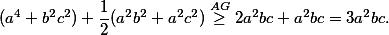
Sečtením tří analogických nerovností skutečně získáme výsledek.
Konkrétně
Sečtením tří analogických nerovností skutečně získáme výsledek.
BakyX | 3. 5. 2011 15:02:29
Ehm..Má tam byť b^2. Prepáčte.
BakyX | 3. 5. 2011 15:01:22
Ahojte..Potreboval by som pomoc pri riešení úlohy zo seriálu Nerovnosti. Je z témy Sčítanie AG. V nerovnostiach som začiatočník a veľmi mi nejdú. Ďakujem za pomoc. Čísla a,b,c sú kladné celé čísla:
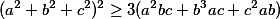
Kenny | 1. 5. 2011 18:58:02
Tak já si pojistím vedení v počtu příspěvků v matematické sekci a sdělím, že jsem doplnil seznam doporučené literatury v matematickém rozcestníku o jména autorů.
Mrkněte na http://mks.mff.cuni.cz/MO.php
Mrkněte na http://mks.mff.cuni.cz/MO.php
zyxcba | 29. 4. 2011 23:25:51
Vážená AG na číslech (x/a), (y/b), (z/c) s váhama a,b,c:
![\frac{x+y+z}{a+b+c}\ge\sqrt[a+b+c]{(\frac{x}a)^a(\frac{y}b)^b(\frac{z}c)^c} \frac{x+y+z}{a+b+c}\ge\sqrt[a+b+c]{(\frac{x}a)^a(\frac{y}b)^b(\frac{z}c)^c}](https://prase.cz/chat/texmaker.php?tex=%5Cfrac%7Bx%2By%2Bz%7D%7Ba%2Bb%2Bc%7D%5Cge%5Csqrt%5Ba%2Bb%2Bc%5D%7B%28%5Cfrac%7Bx%7Da%29%5Ea%28%5Cfrac%7By%7Db%29%5Eb%28%5Cfrac%7Bz%7Dc%29%5Ec%7D&hash=9dda58204dda725b2f30)
abcxyz | 29. 4. 2011 20:18:07
Ahoj, chtěl bych se zeptat, jak vyřešit tuto nerovnost 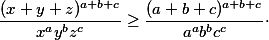 Prý by na to měla stačit AG.
Prý by na to měla stačit AG.
díky
díky
Kenny | 27. 4. 2011 15:00:28
Upozorňuji všechny fanoušky teorie čísel, že se na mathlinks objevil článek k takzvanému "Lifting exponent lemma", což je úplně krutá technika, jak si ušetřit spoustu práce v těžkých úlohách z teorie čísel!
Článek najdete na adrese http://www.artofproblemsolving.com/Forum/view...
Článek najdete na adrese http://www.artofproblemsolving.com/Forum/view...
Kenny | 25. 4. 2011 21:38:59
A velkou cenu 2b již pokořil i Štěpán!
Odměnou mu, krom příslušného dílu čokolády, budiž i to, že obsadil první příspěvek v matematické sekci nového chatu!
Odměnou mu, krom příslušného dílu čokolády, budiž i to, že obsadil první příspěvek v matematické sekci nového chatu!




