Kenny | 29. 5. 2011 14:35:58
Za to značení v trojce bych je fakt zabil :D. Prý S střed úsečky TV :D...
Pepa T. | 29. 5. 2011 14:20:22
Pětka je fakt ďábelská konstanta... To jste věděli, že
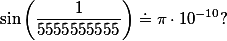
Kuba | 29. 5. 2011 14:19:01
Zadání MO na přístí rok je na internetu zde:http://skmo.sk/
Pepa T. | 25. 5. 2011 13:25:58
A na mathlinks (http://www.artofproblemsolving.com/Forum/view...) se objevila zadání polského celostátka! Můžete se podívat a udělat si srovnání :). Řešení jsou (v polštině) na (http://www.om.edu.pl/).
Pepa T. | 22. 5. 2011 23:41:27
Jinak Myšmaš byl letos fakt docela masakr... Smekám před všemi jedenácti hrdiny, kteří zvládli alespoň jednu úlohu vyřešit na alespoň čtyři body! Takhle náročný byl myšmaš naposledy před pěti lety (tj. ve 25. ročníku). Zájemcům doporučuju obzvláště tehdejší pětku a sedmičku ;).
Štěpán | 19. 5. 2011 18:32:45
jo, stačilo, děkuju
Pepa T. | 18. 5. 2011 23:43:38
Věnuju dokonce (byť schematický) popis řešení: Dokresli připsiště 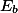 ,
, 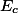 trojúhelníka
trojúhelníka 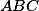 vzhledem k
vzhledem k 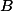 a
a 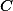 a ukaž, že kružnice opsaná
a ukaž, že kružnice opsaná 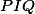 je vlastně kružnicí opsanou
je vlastně kružnicí opsanou 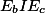 (přímka
(přímka 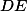 je chordála). A pak si už jen vzpomeň na Feuerbachovu kružnici :). Stačilo? Nebo ještě?
je chordála). A pak si už jen vzpomeň na Feuerbachovu kružnici :). Stačilo? Nebo ještě?
Tonda | 18. 5. 2011 18:58:05
Štěpán: No už vím jak se dělá 3b, dám ti hint jestli chceš :)
Štěpán | 18. 5. 2011 18:33:55
Pepo, nechceš věnovat nějaký hint k 3b?
pavel | 18. 5. 2011 13:15:38
Ja teda nevim, ktery z tech kroku presne wolfram neumi. Nejspis asi proste neumi zkombinovat vsechny tri, ale kazdopadne
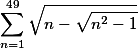
uz zvladne :) (http://www.wolframalpha.com/input/?i=sum_{n%3...)
uz zvladne :) (http://www.wolframalpha.com/input/?i=sum_{n%3...)
Pepa T. | 17. 5. 2011 19:04:49
Tak ať tu ta úloha nesmrdí tak dlouho, tak já popíšu tři triky, které se při řešení použijou:
1) Usměrnit zlomek: vynásobit jeho čitatel i jmenovatel výrazem
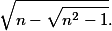
2) Odmocnit druhou mocninu: např.
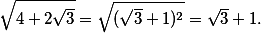
Tady je to podobné, akorát se přišmelí nějaká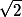 , aby to vyšlo líp. Pak totiž docela funguje, že
, aby to vyšlo líp. Pak totiž docela funguje, že 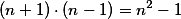 a
a 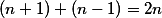 (tohle je ten krok, který wolfram neumí).
(tohle je ten krok, který wolfram neumí).
3) Zteleskopovat: Tím se myslí takový ten trik, že
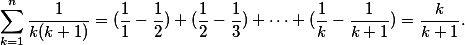
S tímhle návodem už by to nemělo být náročné ;-).
1) Usměrnit zlomek: vynásobit jeho čitatel i jmenovatel výrazem
2) Odmocnit druhou mocninu: např.
Tady je to podobné, akorát se přišmelí nějaká
3) Zteleskopovat: Tím se myslí takový ten trik, že
S tímhle návodem už by to nemělo být náročné ;-).
miso | 16. 5. 2011 17:22:57
kdo bych chtel resit maxima, minima, neco z funkcii najme operacie s funkciami aneb vse co vi nech se ozvi. Dam mu moj ID skype.Najme pre druhakov, tretiakov na strednych skolach.
Mirek Olšák | 13. 5. 2011 22:15:40
Je to tak, taky to uz umim, ale mam pocit, ze Wolfram to v zasade vyresil za mne. Holt v (olympiadni) algebre se tezko hleda Mathematico-vzdorna uloha podobne jako v geometrii geogebro-vzdorna...
Ale poscita se to pekne.
Ale poscita se to pekne.
pavel | 13. 5. 2011 20:27:31
Ale po prvnim kroku uz to Wolfram zvladne :-) (pokud nahodou neznate, urcite vyzkousejte http://www.wolframalpha.com/)
Vejtek | 13. 5. 2011 19:17:20
Ha, pěkný trik, který ani wolfram neumí!
PS: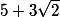
PS:
Pepa T. | 13. 5. 2011 13:18:24
Haha, našel jsem dobrou legrácku, tak se o ní nemůžu nepodělit :).
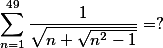
Za správný výsledek je čest a sláva, ale nepište postup, ať to neprokecnete ostatním :).
Za správný výsledek je čest a sláva, ale nepište postup, ať to neprokecnete ostatním :).
Štěpán | 11. 5. 2011 14:05:27
Olin: no to sice jo, ale to už je jen jednoduchá finta...
Mirek: nevím, jestli je platnost oné věty opravdu očividná, každopádně i kdyby byla, tak to neznamená, že je úloha lehká, protože se ještě člověk musí vydat tímto směrem...
Mirek: nevím, jestli je platnost oné věty opravdu očividná, každopádně i kdyby byla, tak to neznamená, že je úloha lehká, protože se ještě člověk musí vydat tímto směrem...
Olin | 11. 5. 2011 12:21:32
Mirek, Štěpán: Samozřejmě je zapotřebí to ještě trochu poupravit, protože Ramseyovka nám neříká, jakou "barvu" ta klika bude mít, zatímco v zadání je "barva" už stanovena.
Miroslav Olšák | 10. 5. 2011 22:05:00
Štěpán: Když myslíš... Ale jestli je platnost oné věty i její použití očividné, tak jak to, že to byla tak nezdolatelná úloha? Jinak, Anička Zavadilová prý to 4b vyřešila, tak jsem zvědavý.
Kenny | 10. 5. 2011 21:33:17
A vítězí Tondaaa, který tak vyřešil jedničku z amerického celostátka 2011!
Ale orgové se nenechávají zahanbit a vypisují druhou výzvu platnou do dnešní půlnoci!
Součet reálných čísel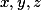 je 0. Dokažte, že platí
je 0. Dokažte, že platí
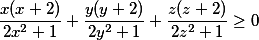
a najděte všechny případy, kdy nastává rovnost.
Dá to někdo za dvě a půl hodiny?
Ale orgové se nenechávají zahanbit a vypisují druhou výzvu platnou do dnešní půlnoci!
Součet reálných čísel
a najděte všechny případy, kdy nastává rovnost.
Dá to někdo za dvě a půl hodiny?




