pavel | 17. 7. 2011 19:49:45
Tak jsem nad tim trochu premyslel... Uz asi castecne rozumim, jak to myslis. Jestli to chapu spravne, tak ty chces, aby 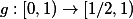 normalne linearne, tj.
normalne linearne, tj.
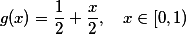
a dalsi intervaly zobrazit "ve stejnem duchu", coz by slo zapsat treba jako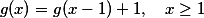 . Funkce
. Funkce 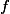 by pak zobrazovala podobne, ale prave do tech "vedlejsich intervalu", tj.
by pak zobrazovala podobne, ale prave do tech "vedlejsich intervalu", tj.
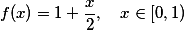
(a dalsi intervaly "ve stejnem duchu").
Myslis to takto?
To by ti potom krasne fungovalo pro racionalni cisla. Nebude ti to ale zase fungovat pro to zadani (b), protoze funkce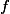 by se snazila zobrazit nekonecnou mnozinu do konecne mnoziny (v intervalu
by se snazila zobrazit nekonecnou mnozinu do konecne mnoziny (v intervalu 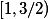 se nachazi pouze jedno cislo tvaru
se nachazi pouze jedno cislo tvaru 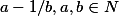 ).
).
Co se tyka tve puvodni otazky - zda existuje bremska dvojice pro kazdou hustou podmnozinu R. Mam nejake duvody se domnivat, ze to bude platit. Myslim si, ze pro docela dost (i pomerne "skaredych") hustych mnozin umim bremskou dvojici najit (casto funguje vzit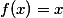 a najit rostouci
a najit rostouci 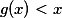 . Najit bremskou dvojici pro nekolik hustych mnozin bylo zatim vzdy snazsi nez ji najit pro mnozinu ze zadani (b) - to je totiz prave ta "neprijemna" mnozina, kde se musi brat
. Najit bremskou dvojici pro nekolik hustych mnozin bylo zatim vzdy snazsi nez ji najit pro mnozinu ze zadani (b) - to je totiz prave ta "neprijemna" mnozina, kde se musi brat 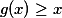 (to se da ukazat).
(to se da ukazat).
Vymyslet obecnou konstrukci (nebo mozna radeji existencni dukaz) pro libovolnou hustou mnozinu se mi ale fakt nechce.
a dalsi intervaly zobrazit "ve stejnem duchu", coz by slo zapsat treba jako
(a dalsi intervaly "ve stejnem duchu").
Myslis to takto?
To by ti potom krasne fungovalo pro racionalni cisla. Nebude ti to ale zase fungovat pro to zadani (b), protoze funkce
Co se tyka tve puvodni otazky - zda existuje bremska dvojice pro kazdou hustou podmnozinu R. Mam nejake duvody se domnivat, ze to bude platit. Myslim si, ze pro docela dost (i pomerne "skaredych") hustych mnozin umim bremskou dvojici najit (casto funguje vzit
Vymyslet obecnou konstrukci (nebo mozna radeji existencni dukaz) pro libovolnou hustou mnozinu se mi ale fakt nechce.
anonym | 17. 7. 2011 11:29:41
no pro racionalní me to prijde jasny ta konstrukce proste prenese racionalni cisla z intervalu na pul intervalu a na tu hustou mnozinu se prave ptam
pavel | 16. 7. 2011 22:48:40
To je bohuzel tak obecny popis, ze me nepriblizuje k odpovedi na tvou puvodni otazku - jestli jde konstrukce provest pro hustou podmnozinu R (nebo aspon pro racionalni cisla).
anonym | 16. 7. 2011 21:49:56
no moje funkce ja sem to resil pred trema dnama takze ten predpis nechci ted znova vymejselt ale je to teoreticky tak ze kdyz vezmu treba cisla z intervalu k až k+1 (k je element celejch cisel)tak funkce g je cely zobrazi do intervalu k+0,5 az k+1 a funkce f do k+1 az k+1,5
pavel | 16. 7. 2011 21:44:25
Jake je tvoje reseni pro racionalni cisla? Nebo mas existencni dukaz?
anonym | 16. 7. 2011 21:21:26
no ja nevim me pride ze pro racionalni to jde a jaky teda mas reseni toho b???
pavel | 16. 7. 2011 21:17:24
Tomu nerozumim, co by melo taky fungovat. Mnozina S v pripade (b) neni husta v R. A ani pro nejakou jednoduchou hustou podmnozinu R, napriklad racionalni cisla, me nenapada, jak primocare rozsirit moje reseni casti (b).
anonym | 16. 7. 2011 20:38:44
presne tak ja se jenom chtel ujistit diky a kdyby se za mnozinu S vzala libovolná mnozina husta v prirozeny topologii na R tak by to taky fungovalo ne??
pavel | 16. 7. 2011 20:22:59
Cau,
(a) neexistuje, (b) existuje. To se mozna dalo trochu cekat uz podle stylu zadani, ale prisla mi to docela pekna uloha. Pokud te zajima hint nebo cele reseni, jeste se ozvi.
(a) neexistuje, (b) existuje. To se mozna dalo trochu cekat uz podle stylu zadani, ale prisla mi to docela pekna uloha. Pokud te zajima hint nebo cele reseni, jeste se ozvi.
anonym | 13. 7. 2011 19:11:55
http://skmo.sk/dokument.php?id=45 vite nekdo odpoved prvni ulohy??
pavel | 7. 7. 2011 13:08:30
Cau,
pokud vydrzis ve cteni serialu, tak na strane 40 uvadime jedno reseni a na strane 50 druhe (skarede, ale primocare). V podstate jde o ulohu IMO 2005, problem 3, takze na internetu jde najit mnoho dalsich podrobnosti (http://www.artofproblemsolving.com/Forum/view...
Pokud bys chtel jen hint, tak jde o to odhadnout jmenovatele tak, aby se zlomky daly secist (a samozrejme aby zaroven nerovnost stale platila :) )
Preju hodne zdaru pri cteni serialu!
pokud vydrzis ve cteni serialu, tak na strane 40 uvadime jedno reseni a na strane 50 druhe (skarede, ale primocare). V podstate jde o ulohu IMO 2005, problem 3, takze na internetu jde najit mnoho dalsich podrobnosti (http://www.artofproblemsolving.com/Forum/view...
Pokud bys chtel jen hint, tak jde o to odhadnout jmenovatele tak, aby se zlomky daly secist (a samozrejme aby zaroven nerovnost stale platila :) )
Preju hodne zdaru pri cteni serialu!
BakyX | 5. 7. 2011 19:11:40
Zdravím..Ako dokázať túto nerovnosť z vášho SviŇského (respektíve PraSečieho) seriálu :) ? http://img685.imageshack.us/img685/428/nerovn... Postačil by mi nejaký hint. Celkom ma štvú tie piate mocniny v menovateľoch. a^5+b^5+c^5 rozložiť neviem a aj tak by to asi nepomohlo..Všimol som si symetriu, to ale nevie, ako v prvom kroku pomôže. Ďakujem za radu.
pavel | 1. 7. 2011 15:17:05
Koukam, ze pres prazdniny se nejak nikomu nechce resit :D Priznavam, ze teda ani me :D
šnEk | 21. 6. 2011 14:20:35
Minulý týden nás Víťa učil brutálně drsnou teorii čísel a jako speciální případ jednoho cvičení tam vypadla věta: Každé celé číslo n takové, že n je kvadratickým zbytkem modulo každé prvočíslo p, je druhou mocninou jiného celého čísla.
Zvládnete to dokázat taky?
Číslo b je kvadratickým zbytkem modulo p, pokud existuje a takové, že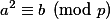
Zvládnete to dokázat taky?
Číslo b je kvadratickým zbytkem modulo p, pokud existuje a takové, že
Miroslav Olšák | 16. 6. 2011 22:05:31
I ty bidaku. Znamy rikas? No mam pocit, ze vymyslet open problem z teorie her nemusi byt zas tak tezke (sachy jsou taky, neni liz pravda).
Ale jinak tu stale zustava (resitelna) uloha o sto studentech. Tak co? Jde to nebo ne?
Ale jinak tu stale zustava (resitelna) uloha o sto studentech. Tak co? Jde to nebo ne?
Rado | 16. 6. 2011 21:27:04
Já už to prozradím: vám všem, co jste věnovali té "mé" úlohy se omlouvám, protože jste pravděpodobně trochu ztráceli čas. Tato úloha je relativně známý otevřený problém a bylo nepravděpodobné, že by na to někdo přišel, ale chtěl jsem si zaexperimentovat a tak jste si někteří alespoň zkusili řešit "pořádný" problém. Omlouvám se a slibuji, že už to nikdy neudělám. Možná ;-D . A teď se zase věnujte "normálním" úlohám!
Kenny | 16. 6. 2011 21:25:54
Ať to řekne sám Rado... :)
Pepa T. | 16. 6. 2011 18:02:50
Kenny, tak už to řekni...
Rado | 8. 6. 2011 19:12:35
Tak když už máme tu sérii "Hry a soutěže", zkuste si (vy, co už máte třeba všechno hotovo) vyřešit jednu úlohu na vyhrávající strategii (ano, všimli jste si správně, úlohu nezadává org, nýbrž prostý účastník - to víte, chtěl jsem si zkusit, jak se při tom ti orgové cítí) :
Máme dva hráče a n - prvkovou množinu (třeba M). V každém tahu si hráč vybere libovolnou neprázdnou podmnožinu M různou od M(nazvěme ji třeba P), ovšem tak, že žádná z předtím vybraných množin nesmí být podmnožinou P. Prohrává ten, kdo už nemůže udělat žádný tah. Určete, kdo (v závislosti na n) má vyhrávající strtegii (začínající, nebo nezačínající hráč?)
Řešení posílejte na nahoře uvedený mail.
Hodně štěstí
Máme dva hráče a n - prvkovou množinu (třeba M). V každém tahu si hráč vybere libovolnou neprázdnou podmnožinu M různou od M(nazvěme ji třeba P), ovšem tak, že žádná z předtím vybraných množin nesmí být podmnožinou P. Prohrává ten, kdo už nemůže udělat žádný tah. Určete, kdo (v závislosti na n) má vyhrávající strtegii (začínající, nebo nezačínající hráč?)
Řešení posílejte na nahoře uvedený mail.
Hodně štěstí
Honza | 6. 6. 2011 17:58:27
Miško> OK, budu používat závorky.




