Pavel Šalom | 25. 9. 2011 14:50:21
Co znamená pravidelné střídání podání? Znamená to, že se střídají přesně po jednom podání, nebo to znamená, že se mohou střídat třeba vždy po třech podáních?
Josef Tkadlec | 25. 9. 2011 01:01:06
Tak to abychom ji využili! :) Neváhejte sem (schovaně) psát nápady, dílčí řešení, komentáře nebo vlastně cokoliv k následující úloze:
Dva hráči (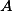 a
a 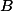 ) hrají proti sobě něco jako tenis. Oba mají nějakou (ne nutně stejnou) pevnou šanci na to, že míček, který sami podávají, vyhrajou. Kdo první vyhraje
) hrají proti sobě něco jako tenis. Oba mají nějakou (ne nutně stejnou) pevnou šanci na to, že míček, který sami podávají, vyhrajou. Kdo první vyhraje  míčků, vyhrává celkově. Podání se střídá podle jednoho ze dvou schémat: Buď pravidelně, nebo vždycky podává ten, kdo vyhrál minulý míček (vždy začíná podávat
míčků, vyhrává celkově. Podání se střídá podle jednoho ze dvou schémat: Buď pravidelně, nebo vždycky podává ten, kdo vyhrál minulý míček (vždy začíná podávat 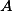 ).
).
Dokažte, že šance hráčů na celkovou výhru nezávisí na volbě schématu.
Dva hráči (
Dokažte, že šance hráčů na celkovou výhru nezávisí na volbě schématu.
Miško | org | 24. 9. 2011 13:20:30
Ahoj, máme pre vás novú feature:
+ skrytý text
+ skrytý text
Šavlík pre vás naprogramoval skrývanie textu!
Josef Tkadlec | 20. 9. 2011 21:50:16
Že jsem se ale musel snažit... A co, bolelo to? :D
Martin Čech | 20. 9. 2011 21:34:48
Pepa mě donutil, abych sem napsal, že jsem to vyřešil bez hintu, a že to čtvrté číslo je 164. Jsou to jediná trojciferná čísla s různými ciframi, která když zapíšeme v desítkovém zápisu ve tvaru ABC, tak platí, že A*BC=C*AB.
Miroslav Olšák | org | 20. 9. 2011 14:04:00
Dobra, tak s hintem uz jsem Pepovu trojcifernou hricku vyresil. Kdo dal?
Zbyněk | 15. 9. 2011 17:18:47
@Pepa: docela zajímavý, že se z té české olympiády dostala do sbírky PEN (stojí za stáhnutí)
http://www.artofproblemsolving.com/Forum/view...
http://www.artofproblemsolving.com/Forum/view...
Josef Tkadlec | 15. 9. 2011 12:36:55
Hrál jsem si tak jednou s trojcifernými čísly, která mají všechny cifry různé, a napadla mě zajímavá vlastnost, kterou by taková čísla mohla mít. Po chvilce počítání jsem zjistil, že existují přesně čtyři čísla s touto vlastností (trojciferná s různými ciframi). Tři z nich jsou 195, 265 a 498. Co je to za vlastnost? Které číslo je to čtvrté? :)
P.S. Předchozí úloha byla (věřte nevěřte) z archivu české matematické olympiády. Můžete se o tom přesvědčit na http://cgi.math.muni.cz/~rvmo/ABC/48/A48s.pdf.
P.S. Předchozí úloha byla (věřte nevěřte) z archivu české matematické olympiády. Můžete se o tom přesvědčit na http://cgi.math.muni.cz/~rvmo/ABC/48/A48s.pdf.
Josef Tkadlec | 9. 9. 2011 15:03:29
Našel jsem dobrou legrácku, tak se musím podělit. Schválně si zkuste, není těžká. A můžete taky tipovat zdroj :).
Ukažte, že pro každé přirozené číslo je hodnota součinu
je hodnota součinu
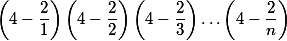
celočíselná.
Ukažte, že pro každé přirozené číslo
celočíselná.
Josef Tkadlec | 5. 9. 2011 18:14:36
Na stránkách http://skmo.sk už je k vidění zadání aktuálního MEMa. A kdo že tam mimo jiné zadal úlohu...? Miško! :)
Miško | org | 30. 8. 2011 22:22:02
Tak už funguje aj TeX vložený do jedného alebo dvoch dolárov, dokonca je rozdiel medzi riadkovým 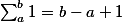 a odstavcovým TeXom:
a odstavcovým TeXom:
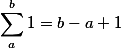
BakyX | 30. 7. 2011 23:47:25
Ďakujem.
šnEk | 29. 7. 2011 00:56:23
BakyX: Já jsem ti nakonec zapomněl odpovědět. V seriálu je jedna podobná rovnice vyřešená, podívej se na úlohu na straně 41 letošního seriálu: http://mks.mff.cuni.cz/common/show.php?title=...
V zásadě jde o to, pravou stranu rozložit na Gaussova prvočísla a levou do tvaru (a+ib)(a-ib). Pak už to půjde snadno.
Jinak Gaussova prvočísla jde samozřejmě i objejít, jedna z těch snazších možností je zkusit rovnici ještě převést do hezčího tvaru
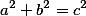 ,
,
tohle řešení se dá najít třeba v archivech olympiády http://cgi.math.muni.cz/~rvmo/ABC/55/A55i.pdf.
Druhá možnost je uhodnout řešení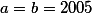 a použít geometrickou metodu z posledního dílu předloňského seriálu.
a použít geometrickou metodu z posledního dílu předloňského seriálu.
Žádný z těch řešení není nic moc extra, ale poprat se s tím dá.
V zásadě jde o to, pravou stranu rozložit na Gaussova prvočísla a levou do tvaru (a+ib)(a-ib). Pak už to půjde snadno.
Jinak Gaussova prvočísla jde samozřejmě i objejít, jedna z těch snazších možností je zkusit rovnici ještě převést do hezčího tvaru
tohle řešení se dá najít třeba v archivech olympiády http://cgi.math.muni.cz/~rvmo/ABC/55/A55i.pdf.
Druhá možnost je uhodnout řešení
Žádný z těch řešení není nic moc extra, ale poprat se s tím dá.
anonym | 28. 7. 2011 21:12:41
ahoj dokazali byste nebo vyvratili tudle nerovnost pro vsechny cely cisla vetsi nez 1 000 000 http://www.wolframalpha.com/input/?_=13117999...
BakyX | 26. 7. 2011 22:17:35
Skúste si ako tréning vyriešiť túto geometrickú úlohu :)
V ostrojuholnom trojuholníku ABC označme D,E,F päty výšok na strany a,b,c. Označme G,H,I stredy kružníc vpísanych trojuholníkom AEF, BDF, CDE. Dokáž, že priamky DG, EH, FI prechádzajú jedným bodom.
V ostrojuholnom trojuholníku ABC označme D,E,F päty výšok na strany a,b,c. Označme G,H,I stredy kružníc vpísanych trojuholníkom AEF, BDF, CDE. Dokáž, že priamky DG, EH, FI prechádzajú jedným bodom.
BakyX | 26. 7. 2011 17:51:16
No viem si to upraviť takto:
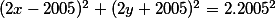
Po substitúcií mám:
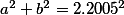
Nedarí sa mi ale odhadnúť niečo normálne pomocou nerovností.
Po substitúcií mám:
Nedarí sa mi ale odhadnúť niečo normálne pomocou nerovností.
šnEk | 25. 7. 2011 23:20:09
Hola!
Vypadá jednoduše, ale nakonec je docela složitá. Jenom napovím, klíčové je upravit rovnici do tvaru
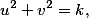
kde k je konstanta a u, v jsou závislé na x a y. Pak se dá použít teorie z letošního seriálu.
Vypadá jednoduše, ale nakonec je docela složitá. Jenom napovím, klíčové je upravit rovnici do tvaru
kde k je konstanta a u, v jsou závislé na x a y. Pak se dá použít teorie z letošního seriálu.
BakyX | 25. 7. 2011 22:35:43
Zdravím..Nepomohol by mi niekto s nasledujúcou rovnicou ?
V obore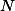 riešte:
riešte: 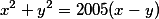
Nemám tušenia :) Vyzerá to jednoducho..Ďakujem za pomoc
V obore
Nemám tušenia :) Vyzerá to jednoducho..Ďakujem za pomoc
anonym | 18. 7. 2011 01:59:41
no jasne presne tak sem to myslel pro ty racionalni cisla a to s tou hustou mnozinou me jenom tak napadlo a fakt diky za tvuj cas
pavel | 17. 7. 2011 19:49:45
Tak jsem nad tim trochu premyslel... Uz asi castecne rozumim, jak to myslis. Jestli to chapu spravne, tak ty chces, aby 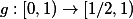 normalne linearne, tj.
normalne linearne, tj.
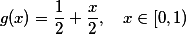
a dalsi intervaly zobrazit "ve stejnem duchu", coz by slo zapsat treba jako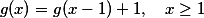 . Funkce
. Funkce 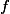 by pak zobrazovala podobne, ale prave do tech "vedlejsich intervalu", tj.
by pak zobrazovala podobne, ale prave do tech "vedlejsich intervalu", tj.
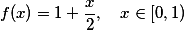
(a dalsi intervaly "ve stejnem duchu").
Myslis to takto?
To by ti potom krasne fungovalo pro racionalni cisla. Nebude ti to ale zase fungovat pro to zadani (b), protoze funkce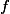 by se snazila zobrazit nekonecnou mnozinu do konecne mnoziny (v intervalu
by se snazila zobrazit nekonecnou mnozinu do konecne mnoziny (v intervalu 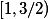 se nachazi pouze jedno cislo tvaru
se nachazi pouze jedno cislo tvaru 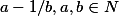 ).
).
Co se tyka tve puvodni otazky - zda existuje bremska dvojice pro kazdou hustou podmnozinu R. Mam nejake duvody se domnivat, ze to bude platit. Myslim si, ze pro docela dost (i pomerne "skaredych") hustych mnozin umim bremskou dvojici najit (casto funguje vzit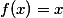 a najit rostouci
a najit rostouci 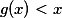 . Najit bremskou dvojici pro nekolik hustych mnozin bylo zatim vzdy snazsi nez ji najit pro mnozinu ze zadani (b) - to je totiz prave ta "neprijemna" mnozina, kde se musi brat
. Najit bremskou dvojici pro nekolik hustych mnozin bylo zatim vzdy snazsi nez ji najit pro mnozinu ze zadani (b) - to je totiz prave ta "neprijemna" mnozina, kde se musi brat 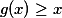 (to se da ukazat).
(to se da ukazat).
Vymyslet obecnou konstrukci (nebo mozna radeji existencni dukaz) pro libovolnou hustou mnozinu se mi ale fakt nechce.
a dalsi intervaly zobrazit "ve stejnem duchu", coz by slo zapsat treba jako
(a dalsi intervaly "ve stejnem duchu").
Myslis to takto?
To by ti potom krasne fungovalo pro racionalni cisla. Nebude ti to ale zase fungovat pro to zadani (b), protoze funkce
Co se tyka tve puvodni otazky - zda existuje bremska dvojice pro kazdou hustou podmnozinu R. Mam nejake duvody se domnivat, ze to bude platit. Myslim si, ze pro docela dost (i pomerne "skaredych") hustych mnozin umim bremskou dvojici najit (casto funguje vzit
Vymyslet obecnou konstrukci (nebo mozna radeji existencni dukaz) pro libovolnou hustou mnozinu se mi ale fakt nechce.




