Chat Prasátek

Matematická sekce

BakyX | 16. 11. 2011 20:30:35

Štěpán: Fakt ďakujem..Btw..Nerovnosti sa naučiť nedajú..Alebo áno ? :D

Štěpán | 16. 11. 2011 19:48:00

Čau. No podle mě se můžeš kubických členů zbavit takovouto susbstitucí:
+ skrytý text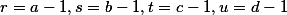

$r=a-1,s=b-1,t=c-1,u=d-1$ , což by mělo být vidět že funguje z binomické věty. Jestli to pomůže vyřešit úlohu jsem nezkoušel, ale vypadá logicky, že by mělo :)

BakyX | 16. 11. 2011 17:00:46

Zdravím. Pomôže mi prosím niekto ? Mám dokázať túto nerovnosť pre reálne čísla 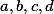$a,b,c,d$ a mám k tomu použiť substitúciu, ktorá "vymaže" kubické členy. Vôbec ma taká nenapadá:

$a+b+c+d=6$
$a^2+b^2+c^2+d^2=12$
$36 \leq 4(a^3+b^3+c^3+d^3)-(a^4+b^4+c^4+d^4)\le 48$

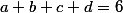
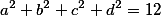
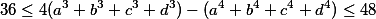
Ďakujem

Josef Tkadlec | 15. 11. 2011 23:12:54

Cenu to rozhodně má -- přednáška se například jen velmi okrajově dotkla toho, jak se shodná zobrazení skládají.

A pak tam taky nepadla ani zmínka o čokoládových úlohách! To jsem zvědavý, za kým odměny za jejich vyřešení poputují ;)...

Štěpán | 15. 11. 2011 23:03:34

Mám dotaz. Když jsem se podíval na záznam z přednášky (mimochodem fakt dobrý ;-)), má ještě cenu číst si seriál nebo bylo vše řečeno?

Pavel Šalom | 15. 11. 2011 16:57:39

Tak pro vsechny, kteri prednasku o zobrazenich nevideli, ale radi by se podivali: na strankach talnetu http://www.talnet.cz/cafe-talnet uz je zaznam (hned prvni odkaz).
Zaznam je mozna jeste lepsi nez online video, protoze kdyz vam unikne nejaka drobnost, muzete se k tomu vratit. Muzu jen doporucit.

Miroslav Olšák | org | 14. 11. 2011 23:37:53

Geogebri obrazky, ktere jsme ukazovali na prednasce k serialu najdete na

http://www.olsak.net/mirek/serial/

Soubory .ggb jsou ke stazeni pro geogebru, .html je online nahled tehoz.

BakyX | 14. 11. 2011 20:16:30

Bolo to good..Dúfam, že bude niekedy prednaška k nerovnostiam. Tie sa naučiť nedajú.

Kenny | 14. 11. 2011 20:13:27

A podle mě to teda bylo dost dobrý!

BakyX | 14. 11. 2011 20:10:37

Bude k stiahnutiu.

Pavel Šalom | 14. 11. 2011 20:03:08

Skoda, ze jste dali s prednaskou vedet az tak pozde, prosvihl jsem to jen o par hodin :(

BakyX | 14. 11. 2011 15:48:48

Aha..Tak to bude tým..No to je smutné teda.

Josef Tkadlec | 14. 11. 2011 14:57:53

Tom, BakyX: Hádám, že jste neoprávněně mlčky předpokládali, že body 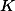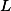$\textstyle K$ , $\textstyle L$ leží na 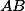$\textstyle AB$ v nějakém konkrétním pořadí. Přestože "myšlenka zůstává", důkazy se v obou možných konfiguracích zřetelně liší, takže je potřeba to rozebrat. Apeluji na všechny, kteří mají z této úlohy 4 body: Zkuste si to.

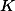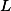BakyX: Případ, kdy body $\textstyle K$ a $\textstyle L$ splynou, byl vyloučen zadáním, takže nebylo třeba se jím zabývat.

BakyX | 14. 11. 2011 14:37:52

Tom: Vyšetril si prípad, keď sú body K, L totožné ? Ja áno..Aj som to pre ten prípad dokázal. A opraveteľ stále našiel chybu !!!

Tom | 14. 11. 2011 12:12:19

Pepa T. no, jak tak koukám, pětadvacítek moc nebude... opravovatel šestky to vzal docela tvrdě... Jsem zvědavej, za co to postrhal, sám ve svym řešení jsem chybu nenašel :D ale aspoň nejsem jedinej...

Josef Tkadlec | 13. 11. 2011 00:10:16

Přednáška k prvnímu dílu seriálu

Slyšte, slyšte! Toto pondělí od 18:00 proběhne v budově MFF v Troji přednáška k prvnímu dílu letošního seriálu. Asi nemusím zdůrazňovat, že to je ideální příležitost, jak se do seriálu pustit :). Všichni jste srdečně zváni.

Pro nepražáky a lenochy mám také dobrou zprávu -- přednáška bude přenášena online! Podrobnosti na http://www.talnet.cz/aktuality.

Josef Tkadlec | 10. 11. 2011 01:22:12

Jestli vážně byla lehká, to se ještě uvidí... Každopádně je tu ještě iKSko (http://kms.sk/iks.php), které se posílá teď v pondělí, tak se do něj všichni pořádně pusťte :).

BakyX | 9. 11. 2011 14:31:44

Pepa T.: Geometrická séria bola neobvykle ľahká..Naschvál znižujete obtiažnosť úloh ? :)

Rado: Skús si dokresliť os nejakej úsečky :) Ale určite sa to dá aj inak.

Rado | 9. 11. 2011 13:21:10

Ahoj, mě by strašně zajímal nějaký hint do osmičky, mohli byste ho sem dát? Dík moc

Josef Tkadlec | 9. 11. 2011 11:23:47

Ahoj Mišo, proti zákonům PraSete ses nijak neprovinil :-D, na žádnou hloupost se neptáš, úplně chápu tvou zvědavost :). Hint následuje.

+ skrytý text

Možných řešení je víc, nejsnazší je asi dokázat, že součet úhlů u $\textstyle A$ a $\textstyle C$ ve čtyřúhelníku $\textstyle ABCD$ je stejný jako součet úhlů u $\textstyle B$ a $\textstyle D$ . Pak budou totiž oba součty rovny $\textstyle 180^\circ$ a bude hotovo. Teď je potřeba si označit čtyři dvojice úhlů, které jsou stejné díky odrazům, a dopočítat. Snad to jako náčrt stačí.

A co vy ostatní? Jak jste se s úlohami poprali? Byl k něčem úvodní text? Kolik bude pětadvacítek? ;)

<< < 1 2 ... 30 31 32 ... 36 37 > >>

Kontakt

email	info (zavináč) prase.cz
pošta	Matematický korespondenční seminář KAM MFF UK Malostranské náměstí 25 118 00 Praha 1

Organizátoři

Matematický korespondenční seminář je organizovaný studenty Matematicko-fyzikální fakulty UK pod záštitou Informatického ústavu UK a Oddělení propagace a mediální komunikace MFF UK.

Partneři

Realizace projektu byla podpořena Ministerstvem školství, mládeže a tělovýchovy

Matematický korespondenční seminář

Kalendář

Z naší fotogalerie

Kontakt

Organizátoři

Partneři