Matematický korespondenční seminář

BakyX: Áno, dokonca pomerne jednoduchý: klikneš na "Lines and polylines" (ikonka má tvar podobný "N"; u mňa je 11. zľava v druhom riadku, prípadne na klávesnici "L"), klikneš jeden koniec a pravým tlačítkom myši vyznačíš koniec druhý. Nie je to priamka v pravom zmysle slova, je to len jej časť, ale ak chceš, vo vlastnostiach čiary si môžeš zadať tvar koncových šípok.

Následne ma ale napadlo, že si možno myslel priamku prechádzajúcu dvoma konkrétnymi bodmi. Tam je postup podobný, opäť nakreslíš čiaru medzi týmito bodmi (postup vyššie, je dobré mať zapnuté "pripínanie k vrcholom" - "snap to vertices", ikona by mala byť hneď prvá po rozlíšení alebo stlač F4). Následne chceme túto spojnicu natiahnuť, aby pokračovala aj za hraničnými bodmi: klikni na "strech objects" (štvrtá ikona druhý riadok alebo "E") a so stlačeným Shiftom natiahni konce na požadovanú dĺžku (sklon by sa zmeniť nemal - to zaručuje práve ten Shift).

Ak by ti to aj napriek tomuto nešlo, určite sa ozvi, kde je problém a pokúsim sa ti pomôcť ešte lepšie :)

Existuje prosím nejaký jednoduchý spôsob, ako v dementom programe IPE 6 urobiť priamku :D ?

Miško, Pítr: Ano, vskutku je to zřejmé, když uvážíme nezápornost uvedených proměnných :-) Zároveň je dobře vidět, kdy vlastně nastane rovnost.

Miško: neviem, či hovoríme o tom istom, ale mne platnosť nerovnosti



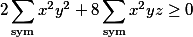
príde naozaj zrejmá - stačí použiť predpoklad zadania, že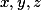 sú nezáporné :)

Možno to platí aj bez tohto predpokladu (to som neskúmal), ale tento dôkaz už zrejmý byť nemusí - a o tom si možno už písal :P

Olin: vcera okolo polnoci som sa snazil uvidiet, preco je to zrejme a nie a nie na to prist. A potom, ked som to roznasobil rucne mi to doslo :)

A teda podla mna to nie je zrejme, (ani jednoduche), ale trilivalne. (A to je rozdiel. :))

Kenny: Ono po té homogenizaci a roznásobení už moc práce není, protože pokud jsem dobře upravoval (teda ne já, samozřejmě nejmenovaný program), tak nakonec vyjde



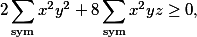
což platí zřejmě.

Olin, Kenny

Ďakujem. Vždy, keď si vyberiem nejakú ľahko vyzerajúcu nerovnosť, vykľuje sa z nej niečo takéto. Seriál som prečítal po Jensenovu nerovnosť.

BakyX: Zkušené oko vidí, že nerovnost nemůže odolat težkým zbraním.

Rozhodně ji lze řešit takto:

1) Dle Olina, tj. homogenizovat, roznásobit, Muirheadovat-Schurovat (třetí díl seriálu)

2) Dosadit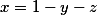 , roznásobit a čtvercovat (víme, kdy chceme rovnost...)

3) Dosadit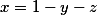 , použít symetrickou substituci a posléze s ní čachrovat podobně jako je to ve druhém díle seriálu.

Nad elegantním řešením se zamyslím (Tondo, máš něco?)

Jinak tato nerovnost je svoji obtížností nad úrovní celostátního kola.

A též doporučuji přečtení seriálu. Věřim, že to není jen výčet metod, ale že je možné tam načerpat i docela dost intuice.

BakyX: Není to příliš elegantní, ale už jsi to zkoušel homogenizovat? Doufám ale, že někdo přijde s lepším nápadem.

Niekedy nie je problém ochota učiteľa pripravovať na MO, ale skôr jeho schopnosti riešiť úlohy z MO.

Dal by mi niekto hint k tejto nerovnosti ? Pre nezáporné čísla x,y,z platí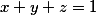 . Mám dokázať:



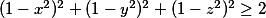
Nerovnosti sa nenaučím, nech robím, čo robím. Ďakujem

vraciam spat, az teraz som tam to videl, fakt som slepy prapacte

v 32 ulohe ve aktualnej serie o geometrickych zobrazenia je velkost usecky BF ? Co je bod F? priesecnik coho?

Ahoj, mám menší problém s jednou kombinatorickou úlohou vlastní výroby, ke které se mi nedaří najít řešení. Kdyby někdo věděl, jak na ni, byl bych vděčný i třeba jen za malou nápovědu.

Zadání: Máme populaci N lidí, ve které je K nemocných. Jak velkou skupinu (zlomek N) musím vybrat, abych měl 90% pravděpodobnost, že procentuální podíl nemocných v mém výběru bude s odchylkou +- 10% odpovídat podílu K/N?

Zrovna mě napadla taková úloha, která je sice velmi jednoduchá, ale se mi líbí:
Mějme pravidelný šestiúhelník a rozdělíme ho na shodné rovnostranné trojúhelníky. Dokažte, že úsečka spojující dvě protější strany, která neprochází žádným vrcholem trojúhelníků, prochází sudým počtem malých trojúhelníků.

Mark: Asi máš šťastie na školu, ktorú navštevuješ. Na gymnáziu, kam som chodil ja, sa nikto nestaral o to, aby matematiku vyučoval viac, ako mu určovali osnovy, a o nejakom matematickom krúžku sa myslím ani neuvažovalo.

Predpokladám, že podobná situácia je na viacerých školách, hlavne na tých menších, kde nie je veľa učiteľov, ktorí teda ani nemajú veľmi záujem o rozvíjanie schopností študentov...

Tak ale mal by byť na škole taký krúžok aj keď to nie je matematické gymnázium. Nevidím dôvod, prečo by na to nemal mať čas 2 hodiny týždenne. Učiteľa nemôže žiadna učebnica alebo články nahradiť. Jeho úloha je nenahraditeľná.

Uf, ucitel ve skole to urcite nebude mit cas ukazovat, pokud nejsi na matematickem gymplu...
Prvni dil serialu o nerovnostech ukazuje opravdu jen zakladni metody bez kterych jsou ulohy na urovni celostatka temer neresitelne - konkretne se tam objevuji jen AG a Cauchy.

BakyX: Neviem, čo ti povedia vysokoškoláci, ale ak sa chceš zúčastniť aj matematickej olympiády kategórie A(keďže si spomínal celoštátne kolo), tak určite treba vedieť počítať nerovnosti, v ktorých sa využíva AG nerovnosť. Cauchyho nerovnosť sa tiež môže hodiť. Takže to zo seriálu by som si prečítal. A plus je dobré sa pozrieť na KA, GH a KH nerovnosti. Ale toto všetko by vám mal ukázať aj učiteľ na škole.

Ďakujem. Seriál som čítať skúšal..Ale..Mne nejde o to naučiť sa 100 rôznych metód. Chcel by som ako tak zvládnúť tie základne, aby ma nezabila nerovnosť v krajskom kole, prípadne keby sa stali 4 zázraky, na celoštátku. Napríklad tú, čo bola tento rok by som nezvládol.

BakyX: zkousel jsi uz cist nas serial o nerovnostech (v archivu)? Mimochodem jeho aktualnejsi verze se da najit na http://atrey.karlin.mff.cuni.cz/~paves/serial...
Chce to docela trpelivost, ale myslim, ze by te to mohlo zajimat.