Mark Daniel | 10. 12. 2011 22:22:17
Ospravedlňujem sa Vám, ak som to mal dať do skrytého textu.
Mark Daniel | 10. 12. 2011 22:21:21
Pavel, Mirek: Ďakujem za odpoveď.
BakyX, spoločný násobok: Celkom by ma zaujímalo, kde si našiel tento príklad.
Vychádzam z toho, že 3 na n-tú je presne 1,5 na n-tú viac ako 2 na n-tú:
Vieme, že násobky 1,2,3,4,6,8 určite nebudú spoločným násobkom, lebo toto všetko sú násobky alebo 2, alebo 3 a tým minimálne jedna zo zátvoriek nie je. To znamená, že nejaká zo zátvoriek je násobok 5,7 a ďalších prvočísiel. Z toho vyplýva, že jedna zo zátvoriek sa nepochybne končí číslicami 1,3,5,7 alebo 9 ako aj druhá. A spoločný násobok bude nejaké prvočíslo.
Pre prvú zátvorku:
Ak sa končí číslicou 1: tak potom samotná mocnina 2 sa končí číslicou 0. Ale taká neexistuje.
Ak sa končí číslicou 3: Tak potom samotná mocnina čísla 2 sa končí číslicou 1. Taká neexistuje.
Ak sa končí číslicou 5: Tak potom samotná mocnina 2 sa končí číslicou 4. To je možné. Toto si zatiaľ odložme do šuflíka.
Ak sa končí číslicou 7: Tak potom samotná mocnina 2 sa končí číslicou 6. To je možné.
Ak sa končí číslicou 9: Tak potom samotná mocnina 2 sa končí číslicou 8, čo je možné.
Aj tieto dve možnosti si odložme.
Teda vidíme, že má zmysel uvažovať iba o tých tvaroch prvej zátvorky, ktoré sa končia číslicami: 5,7,9. Keďže 5 a 7 sú prvočísla, tak tu by sa spoločný násobok končil alebo číslicou 5 alebo 7, alebo číslicou 1. U čísla 9 má zmysel uvažovať o tom, že spoločný násobok sa končí číslicou alebo 1, alebo 9, alebo 3.
A teraz sa pozrime na to, kedy sa končí mocnina čísla 2 číslicou 4. To, ako ste isto vypočítali aj v školskom kole MO A, platí vtedy, keď exponent má tvar: 2+4x.
A keď má exponent takýto tvar, potom 3 umocnené týmto exponentom sa končí číslicou 9. Teda jedna zátvorka sa končí číslicou 5, druhá číslicou 9+2=11. To znamená, že spoločný deliteľ by sa musel končiť číslicou 5 alebo 1. Ale pritom neexistuje možnosť, kde ........m*........5=......1(toto je možnosť, kde spoločný násobok, ktorý sa končí číslicou 5 sme vynásobili nejakým číslom, ktorý sa končí číslicou m a dostali druhú zátvorku) , pričom m leží v intervale 1-10. Ešte treba zvážiť možnosť, ak sa spoločný násobok končí číslicou 1. To zatiaľ necháme tak.
Ak sa mocnina čísla 2 končí číslicou 6, tak exponent má tvar n=4+4x. Spoločný násobok sa, samozrejme, končí číslicou alebo 1, alebo 7. Pritom 3 umocnené exponentom v tvare 4+4x sa končí číslicou 1, teda druhá zátvorka sa končí číslicou 1+2=3. Teda opäť sa spoločný násobok musí končiť číslicou 1.
Ak sa mocnina čísla 2 končí číslicou 8, tak exponent má tvar n=3+4x. A číslo 3 umocnené takýmto exponentom sa končí číslicou 7, teda druhá zátvorka sa končí číslicou 7+2=9. Teraz nastal zaujímavý prípad, keď sa obe zátvorky končia rovnakou číslicou. Spoločný deliteľ sa musí končiť číslicami 1,3 alebo 9. Ak sa spoločný násobok končí číslicou 9, znamená to, že aj rozdiel jednej a druhej zátvorky je deliteľný číslom 9. Pritom rozdiel má na konci číslo 0. Ak od tohto čísla odčítame jednu alebo druhú zátvorku, tak výsledné číslo bude mať na konci číslicu 1. Teraz od tohto čísla opäť odčítajme niektorú zo zátvoriek a na konci nám zostalo číslo 2. A tento výsledný rozdeľ musí byť deliteľný číslom, ktoré ma na konci číslicu 9. Ale nie je možné, aby súčin dvoch číslic, kde na konci jedného je 9, dal na číslo, na ktorého konci je číslica 2. Teda túto možnosť tiež vylúčime.
Takže počet možností bol zredukovaný iba možnosti, kde sa spoločný násobok končí číslicou 3 alebo 1. Skúste teda nad týmto pouvažovať.
Zoberme si možnosť, kde sa zátvorky končí číslicou 9. Vieme, že 3 na n-tú je 1,5 na n-tú viac ako 2 na n-tú. Teda sme schopný vynásobiť prvú zátvorku istým číslom tak, aby nám vznikla druhá zátvorka. Vieme, že obe zátvorky sa končia číslicou 9. A o čísle, ktoré sa končí číslicou 9 vieme, že ho musíme vynásobiť aspoň 11x, aby výsledný súčin mal na konci opäť číslicu 9. Teda, násobky čísla, ktoré sa končí číslicou 9, treba násobiť prirodzenými mocninami čísla 11, keď chceme, aby sa výsledný súčin končil číslicou 9. Pritom 1,5 na n-tú nikdy nebude prirodzená mocnina čísla 11. Teda túto možnosť vylúčime.
Zostala posledná možnosť. Keď je spoločný násobok prvočíslo končiace sa číslicou 1.
Ak sa prvá zátvorka končí číslicou 5 a druhá číslicou 1, tak potom:
Ak máme prvé číslo, ktoré sa končí číslicou 5 a chceme, aby po výsledný súčin končil číslicou 1, tak potom číslo, ktorým vynásobíme prvé číslo, musí mať sa desatinnou čiarkou túto hodnotu: .....,20. Ale existuje mocnina čísla 1,5, ktorá sa takto končí? Skúste nad tým pouvažovať.
Ak sa prvá zátvorka končí číslicou 7 a druhá číslicou 3:
Ak máme číslo, ktoré sa končí číslicou 7 a chceme, aby po vynásobení číslom A, bol výsledný súčin číslo končiace sa číslicou 3, tak potom A musí mať za desatinnou čiarou: ......,1/(7/3). Pritom 7/3 je racionálne číslo, teda (aspoň si myslím) aj podiel 1/(7/3) bude iba racionálne číslo. Pritom mocnina 1,5 nikdy nie je racionálne číslo, pretože neustále násobíme číslo, ktoré má ukončený desatinný rozvoj. Teda aj túto možnosť vylúčime. A toto bola posledná možnosť, ktorá zostala. Teda definitívne môžeme povedať, že okrem čísla 1 nemajú tieto dva výrazy spoločného deliteľa.
Niečo som prehliadol?
BakyX, spoločný násobok: Celkom by ma zaujímalo, kde si našiel tento príklad.
Vychádzam z toho, že 3 na n-tú je presne 1,5 na n-tú viac ako 2 na n-tú:
Vieme, že násobky 1,2,3,4,6,8 určite nebudú spoločným násobkom, lebo toto všetko sú násobky alebo 2, alebo 3 a tým minimálne jedna zo zátvoriek nie je. To znamená, že nejaká zo zátvoriek je násobok 5,7 a ďalších prvočísiel. Z toho vyplýva, že jedna zo zátvoriek sa nepochybne končí číslicami 1,3,5,7 alebo 9 ako aj druhá. A spoločný násobok bude nejaké prvočíslo.
Pre prvú zátvorku:
Ak sa končí číslicou 1: tak potom samotná mocnina 2 sa končí číslicou 0. Ale taká neexistuje.
Ak sa končí číslicou 3: Tak potom samotná mocnina čísla 2 sa končí číslicou 1. Taká neexistuje.
Ak sa končí číslicou 5: Tak potom samotná mocnina 2 sa končí číslicou 4. To je možné. Toto si zatiaľ odložme do šuflíka.
Ak sa končí číslicou 7: Tak potom samotná mocnina 2 sa končí číslicou 6. To je možné.
Ak sa končí číslicou 9: Tak potom samotná mocnina 2 sa končí číslicou 8, čo je možné.
Aj tieto dve možnosti si odložme.
Teda vidíme, že má zmysel uvažovať iba o tých tvaroch prvej zátvorky, ktoré sa končia číslicami: 5,7,9. Keďže 5 a 7 sú prvočísla, tak tu by sa spoločný násobok končil alebo číslicou 5 alebo 7, alebo číslicou 1. U čísla 9 má zmysel uvažovať o tom, že spoločný násobok sa končí číslicou alebo 1, alebo 9, alebo 3.
A teraz sa pozrime na to, kedy sa končí mocnina čísla 2 číslicou 4. To, ako ste isto vypočítali aj v školskom kole MO A, platí vtedy, keď exponent má tvar: 2+4x.
A keď má exponent takýto tvar, potom 3 umocnené týmto exponentom sa končí číslicou 9. Teda jedna zátvorka sa končí číslicou 5, druhá číslicou 9+2=11. To znamená, že spoločný deliteľ by sa musel končiť číslicou 5 alebo 1. Ale pritom neexistuje možnosť, kde ........m*........5=......1(toto je možnosť, kde spoločný násobok, ktorý sa končí číslicou 5 sme vynásobili nejakým číslom, ktorý sa končí číslicou m a dostali druhú zátvorku) , pričom m leží v intervale 1-10. Ešte treba zvážiť možnosť, ak sa spoločný násobok končí číslicou 1. To zatiaľ necháme tak.
Ak sa mocnina čísla 2 končí číslicou 6, tak exponent má tvar n=4+4x. Spoločný násobok sa, samozrejme, končí číslicou alebo 1, alebo 7. Pritom 3 umocnené exponentom v tvare 4+4x sa končí číslicou 1, teda druhá zátvorka sa končí číslicou 1+2=3. Teda opäť sa spoločný násobok musí končiť číslicou 1.
Ak sa mocnina čísla 2 končí číslicou 8, tak exponent má tvar n=3+4x. A číslo 3 umocnené takýmto exponentom sa končí číslicou 7, teda druhá zátvorka sa končí číslicou 7+2=9. Teraz nastal zaujímavý prípad, keď sa obe zátvorky končia rovnakou číslicou. Spoločný deliteľ sa musí končiť číslicami 1,3 alebo 9. Ak sa spoločný násobok končí číslicou 9, znamená to, že aj rozdiel jednej a druhej zátvorky je deliteľný číslom 9. Pritom rozdiel má na konci číslo 0. Ak od tohto čísla odčítame jednu alebo druhú zátvorku, tak výsledné číslo bude mať na konci číslicu 1. Teraz od tohto čísla opäť odčítajme niektorú zo zátvoriek a na konci nám zostalo číslo 2. A tento výsledný rozdeľ musí byť deliteľný číslom, ktoré ma na konci číslicu 9. Ale nie je možné, aby súčin dvoch číslic, kde na konci jedného je 9, dal na číslo, na ktorého konci je číslica 2. Teda túto možnosť tiež vylúčime.
Takže počet možností bol zredukovaný iba možnosti, kde sa spoločný násobok končí číslicou 3 alebo 1. Skúste teda nad týmto pouvažovať.
Zoberme si možnosť, kde sa zátvorky končí číslicou 9. Vieme, že 3 na n-tú je 1,5 na n-tú viac ako 2 na n-tú. Teda sme schopný vynásobiť prvú zátvorku istým číslom tak, aby nám vznikla druhá zátvorka. Vieme, že obe zátvorky sa končia číslicou 9. A o čísle, ktoré sa končí číslicou 9 vieme, že ho musíme vynásobiť aspoň 11x, aby výsledný súčin mal na konci opäť číslicu 9. Teda, násobky čísla, ktoré sa končí číslicou 9, treba násobiť prirodzenými mocninami čísla 11, keď chceme, aby sa výsledný súčin končil číslicou 9. Pritom 1,5 na n-tú nikdy nebude prirodzená mocnina čísla 11. Teda túto možnosť vylúčime.
Zostala posledná možnosť. Keď je spoločný násobok prvočíslo končiace sa číslicou 1.
Ak sa prvá zátvorka končí číslicou 5 a druhá číslicou 1, tak potom:
Ak máme prvé číslo, ktoré sa končí číslicou 5 a chceme, aby po výsledný súčin končil číslicou 1, tak potom číslo, ktorým vynásobíme prvé číslo, musí mať sa desatinnou čiarkou túto hodnotu: .....,20. Ale existuje mocnina čísla 1,5, ktorá sa takto končí? Skúste nad tým pouvažovať.
Ak sa prvá zátvorka končí číslicou 7 a druhá číslicou 3:
Ak máme číslo, ktoré sa končí číslicou 7 a chceme, aby po vynásobení číslom A, bol výsledný súčin číslo končiace sa číslicou 3, tak potom A musí mať za desatinnou čiarou: ......,1/(7/3). Pritom 7/3 je racionálne číslo, teda (aspoň si myslím) aj podiel 1/(7/3) bude iba racionálne číslo. Pritom mocnina 1,5 nikdy nie je racionálne číslo, pretože neustále násobíme číslo, ktoré má ukončený desatinný rozvoj. Teda aj túto možnosť vylúčime. A toto bola posledná možnosť, ktorá zostala. Teda definitívne môžeme povedať, že okrem čísla 1 nemajú tieto dva výrazy spoločného deliteľa.
Niečo som prehliadol?
Miroslav Olšák | org | 10. 12. 2011 18:53:01
Ja otazku chapu, Mark chce spocitat GCD v Bakyxove prikladu pomoci Euklidova algoritmu. Problem je, ze nevi, kolikanasobek toho (2^n+1) by mel odecist.
No, ja to taky nevim. Jasne, ze to je zhruba 1,5^n, ale toho vubec neumim vyuzit. Uz treba proto, ze to ani neni cele cislo. Nicmene obecne se mi zda, ze tudy spis cesta nevede.
No, ja to taky nevim. Jasne, ze to je zhruba 1,5^n, ale toho vubec neumim vyuzit. Uz treba proto, ze to ani neni cele cislo. Nicmene obecne se mi zda, ze tudy spis cesta nevede.
Pavel Šalom | 10. 12. 2011 18:34:15
To bude vypadat jako dost odbyta odpoved, ale nenapada me, jak odpovedet lepe.
 je priblizne
je priblizne  -krat vetsi nez
-krat vetsi nez 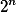 a prislusny rozdil je (ac se to mozna nezda) priblizne
a prislusny rozdil je (ac se to mozna nezda) priblizne  (ve smyslu
(ve smyslu  ).
).
Mozna jsem ale otazku nepochopil spravne.
Mozna jsem ale otazku nepochopil spravne.
Mark Daniel | 10. 12. 2011 17:36:34
Existuje nejaký spôsob ako všeobecne zapísať približne koľkokrát je mocnina čísla 3 umocnená na n-tú, väčšia ako mocnina čísla 2 umocnená na n-tú. Alebo aký je rozdiel týchto dvoch mocnín?
Miroslav Olšák | org | 10. 12. 2011 15:36:45
teorie cisel (stale jen dohady):
+ skrytý text
+ skrytý text
Otestoval jsem, ze pripadne GCD by nebylo delitelne zadnym prvocislem mensim nez milion. A jeste jsem malinko vylepsil Kennyho "protipriklad":
http://www.wolframalpha.com/input/?i=Table[Po...
Nicmene netusim, jestli Bakyxovo tvrzeni plati, ani jak by se na nej dalo jit. V tomhle to je to pro mne trochu jak Collatz.
http://www.wolframalpha.com/input/?i=Table[Po...
Nicmene netusim, jestli Bakyxovo tvrzeni plati, ani jak by se na nej dalo jit. V tomhle to je to pro mne trochu jak Collatz.
Miško | org | 10. 12. 2011 15:24:03
Teoria cisel:+ skrytý text
Podla mna je to tiez tazka uloha. Napadol mi jeden pristup, mozno sa niekto z orgov chyti: Ak je prvocislo 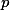 spolocny delitel, tak polynom
spolocny delitel, tak polynom  ma modulo
ma modulo 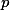 korene
korene 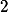 a
a 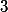 .
.
Kenny | 10. 12. 2011 14:25:02
teorie čísel:
+ skrytý text
+ skrytý text
Toho jsem se přesně bál... Ono je totiž pro každé n "dost pravděpodobné", že ta čísla budou nesoudělná. Klidně se ale může stát něco jako tu
http://www.wolframalpha.com/input/?i=Table%5B... [/link]
http://www.wolframalpha.com/input/?i=Table%5B... [/link]
Mark Daniel | 10. 12. 2011 13:18:42
Musím povedať, že MKS slúži okrem iného naozaj aj na zlepšenie matematických zručností, ktoré sa dajú využiť pri matematickej olympiáde. Know-how z riešenia 6. úlohy 3. podzimní série sa mi úžasne hodilo pri riešení 3. úlohy školského kola MO A.
Štěpán | 10. 12. 2011 12:47:34
geometrie:
+ skrytý text
teorie čísel:
+ skrytý text
+ skrytý text
Jelikož  je těžnice, tak obsahy
je těžnice, tak obsahy  a
a  jsou stejně velké. Obsah trojúhelníka můžeme vyjádřit vzorečkem
jsou stejně velké. Obsah trojúhelníka můžeme vyjádřit vzorečkem  , kde
, kde  jsou postupně obsah, poloměr kružnice vepsané a polovina obvodu trojúhelníka. Platí tedy:
jsou postupně obsah, poloměr kružnice vepsané a polovina obvodu trojúhelníka. Platí tedy:
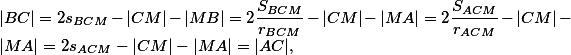
přičemž jsme využívali, že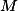 je střed kružnice opsané trojúhelníka
je střed kružnice opsané trojúhelníka 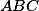 (jedná se o pravoúhlý trojúhelník) a tedy
(jedná se o pravoúhlý trojúhelník) a tedy  . Vzhledem k tomu, že
. Vzhledem k tomu, že  je tím pádem i výška, plyne, že obsah čtverce je:
je tím pádem i výška, plyne, že obsah čtverce je:  a obsah trojúhelníka
a obsah trojúhelníka 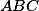 bude vzhledem k tomu
bude vzhledem k tomu  .
.
přičemž jsme využívali, že
teorie čísel:
+ skrytý text
Tak bych spíš řekl, že to platit bude: http://www.wolframalpha.com/input/?i=Table%5B...
Kenny | 10. 12. 2011 12:30:21
K té geometrii:
+ skrytý text
A k té teorii čísel:
+ skrytý text
+ skrytý text
Úloha z podobného soudku je AIME 2010
http://www.artofproblemsolving.com/Forum/reso...
http://www.artofproblemsolving.com/Forum/reso...
A k té teorii čísel:
+ skrytý text
Tipuju, že to neplatí. Nějak nevidím důvod k opaku.
Pokud by to přeci mělo platit, byla by to brutálně těžká úloha. Spíš vědecký problém. Nebo mě nějaký zručný číselný (či spíš grupový?) teoretik vyvede z omylu?
Pokud by to přeci mělo platit, byla by to brutálně těžká úloha. Spíš vědecký problém. Nebo mě nějaký zručný číselný (či spíš grupový?) teoretik vyvede z omylu?
BakyX | 9. 12. 2011 21:06:53
Zdravím. Skúste si vyriešiť túto peknú geometrickú úlohu:
+ skrytý text
Fakt sa teším na tie geniálne trojriadkové riešenia, čo tu od vás padnú :)
+ skrytý text
Označme 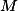 vnútorný bod prepony
vnútorný bod prepony 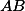 pravouhlého trojuholníka
pravouhlého trojuholníka 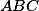 . Predpokladajme, že kružnice vpísané trojuholníkom
. Predpokladajme, že kružnice vpísané trojuholníkom  a
a  sú zhodné. Rozhodnite, či je väčší obsah trojuholníka
sú zhodné. Rozhodnite, či je väčší obsah trojuholníka 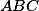 alebo obsah štvorca zostrojeného nad úsečkou
alebo obsah štvorca zostrojeného nad úsečkou 
Fakt sa teším na tie geniálne trojriadkové riešenia, čo tu od vás padnú :)
BakyX | 8. 12. 2011 23:14:34
Zdravím. Ako ukázať že pre prirodzené číslo  sú výrazy
sú výrazy  a
a  nesúdeliteľné ? Ďakujem za odpoveď.
nesúdeliteľné ? Ďakujem za odpoveď.
Miroslav Olšák | org | 8. 12. 2011 21:21:09
Rado, hint na osmicku: Rozdel pravidelny 2011-uhelnik na 2012 konvexnich mnohouhelniku, aby kazda primka protla (mela spolecny bod) max 3 z nich.
Josef Tkadlec | 8. 12. 2011 20:15:02
Ahojte,
jelikož už je po termínu první seriálové série, sepsal jsem jakési návody k řešením čokoládových úloh (stejně teď všichni pilně řešíte KSko, že :)...). Můžete se pokochat a plácnout se do čela.
KSko, že :)...). Můžete se pokochat a plácnout se do čela.
http://atrey.karlin.mff.cuni.cz/~pepat/PraSe/...
Rado: a
a  .
.
jelikož už je po termínu první seriálové série, sepsal jsem jakési návody k řešením čokoládových úloh (stejně teď všichni pilně řešíte
http://atrey.karlin.mff.cuni.cz/~pepat/PraSe/...
Rado:
Rado | 8. 12. 2011 20:06:59
Mark Daniel: Omlouvám se, je to trochu matoucí. 100101111...101101 je (téměř) náhodná posloupnost jedniček a nul.
Jinak zbytek toho,, cos napsal, jsem moc nepochopil. Doporučuji ti obrátit se na orgy - já mám talent na dělání chyb, možná jsem uvažoval úplně špatně (koneckonců, jen tenhle rok jsem tři úlohy naprosto zvoral protože jsem si blbě přečetl zadání, takže na to co píšu moc nespoléhej)
btw: pořád mi nikdo neodpověděl na žádost o hint na osmičku
Jinak zbytek toho,, cos napsal, jsem moc nepochopil. Doporučuji ti obrátit se na orgy - já mám talent na dělání chyb, možná jsem uvažoval úplně špatně (koneckonců, jen tenhle rok jsem tři úlohy naprosto zvoral protože jsem si blbě přečetl zadání, takže na to co píšu moc nespoléhej)
btw: pořád mi nikdo neodpověděl na žádost o hint na osmičku
Miso z PO | 8. 12. 2011 18:57:32
vysledok dobry, postup zly iny algorytmus
Mark Daniel | 8. 12. 2011 18:24:44
Rado: K tomu a+100101111...101101=2a. To je len jedno z riešení? Ak som dobre pochopil úlohu, tak som uvažoval tak nejak, že jediné číslo, ku ktorému keď pripočítam číslo 1, sa zväčší na dvojnásobok, je 1. Teda riešením je počet kombinácii jednotiek a dvojok na mieste jednotiek až 99-tok.
Mark Daniel | 8. 12. 2011 18:20:29
A čo ako? Nejaké povrchné zadanie. Ja si myslím, že to je číslo 33. Ako jediné nie je druhá mocnina prirodzeného čísla. Neviem, s čím iným uvažovať, dve sú násobok čísla 11, dve čísla 100 a 10, ale to z toho neviem, či vyplýva niečo priamo k riešeniu.
Miso z PO | 8. 12. 2011 17:56:55
Tu je jedna úloha:
http://forum.matweb.cz/viewtopic.php?id=38047
http://forum.matweb.cz/viewtopic.php?id=38047




