Josef Tkadlec | 17. 12. 2011 13:24:36
Na podnět Mirka: čtverce o úlohu zpátky se neměly překrývat, jinak je to z hlavy už trochu těžší (je tam nějaké počítání). Jelikož už máme další úlohu, doplním k tamté pro úplnost metodu, jak se dá na výsledek pohodlně přijít.
+ skrytý text
Olin: To jsi asi na minulém sousu nebyl na Martinině přednášce o rozkladech ;) (v knihovně na http://mks.mff.cuni.cz/library/library.php?ca...).
+ skrytý text
Úhlopříčky 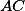 a
a  jsou rovnoběžné, takže obsah trojúhelníku
jsou rovnoběžné, takže obsah trojúhelníku  je stejný jako obsah trojúhelníku
je stejný jako obsah trojúhelníku  , což je půlka prvního čtverce. Velikost druhého čtverce nerozhoduje.
, což je půlka prvního čtverce. Velikost druhého čtverce nerozhoduje.
Olin: To jsi asi na minulém sousu nebyl na Martinině přednášce o rozkladech ;) (v knihovně na http://mks.mff.cuni.cz/library/library.php?ca...).
Olin | org | 17. 12. 2011 00:06:24
Rado: Vzoreček jsem neznal, docela mne překvapil :)
Rado | 16. 12. 2011 21:17:11
Ahoj, narazil jsem na jednu nerovnost, o které myslím , že má moc hezké řešení (pokud znáte jeden vcelku jednoduchý vzoreček). Schválně, zkuste to: pro různá kladná čísla dokažte

Miroslav Olšák | org | 16. 12. 2011 19:19:49
Tak jestli jsem si to dobre predstavil, tak
+ skrytý text
Ale je to z hlavy docela drsne. Nejakou dobu jsem nad tim premyslel a pak jsem si vsimnul, ze bod B je spolecny.
+ skrytý text
2 (pokud se neprekryvaji) nebo 14
Ale je to z hlavy docela drsne. Nejakou dobu jsem nad tim premyslel a pak jsem si vsimnul, ze bod B je spolecny.
Josef Tkadlec | 16. 12. 2011 17:18:39
Narazil jsem na docela vtipnou geometrii, musím se podělit :).
V rovině jsou dány čtverce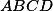 a
a  tak, že
tak, že  ,
,  a
a 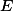 leží v přímce a
leží v přímce a 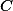 leží na úsečce
leží na úsečce 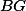 . První čtverec má stranu délky 2, druhý 8. Z hlavy určete obsah trojúhelníka
. První čtverec má stranu délky 2, druhý 8. Z hlavy určete obsah trojúhelníka  .
.
V rovině jsou dány čtverce
Kuba | 14. 12. 2011 19:40:18
Jak se říká: "Když to nejde po zlým, zkusíme to po dobrým..." Bohužel mě ale žádné takové dobré řešení nenapadá. Ještě chci poděkovat všem, kteří se nějak dívali na mou úlohu a hlavně Mirkovi za krásné grafické znázornění.
Miroslav Olšák | org | 12. 12. 2011 23:02:33
Uz mi to beha rychleji, otestovano do p=200000033. Ta uloha nejak vzdoruje hrube sile :(
Miroslav Olšák | org | 12. 12. 2011 19:16:57
taky jsem trochu zkousel, a mam podobnou spatnou zpravu:
pokud prvocislo deli i
i  , tak je vetsi nez 14200001. Tim toto testovani koncim, nicmene kdyby nekdo umel rychle (rychleji nez linearne) najit rad dvojky modulo p, dalo by se dostat do vyssich cisel.
, tak je vetsi nez 14200001. Tim toto testovani koncim, nicmene kdyby nekdo umel rychle (rychleji nez linearne) najit rad dvojky modulo p, dalo by se dostat do vyssich cisel.
pokud prvocislo deli
Olin | org | 12. 12. 2011 18:30:30
Trochu jsem to zkoušel, bohužel mám jen špatnou zprávu:
 pro
pro  .
.
Mark Daniel | 11. 12. 2011 22:36:05
BakyX: Takže sa nevynašiel. Asi neuspel s touto myšlienkou.
Keď hovoríš, že to ľahko overíš pomocou Euklidovho algoritmu, myslíš tým iba prípad, keď jedna zo zátvoriek je deliteľná číslom 25?
Keď hovoríš, že to ľahko overíš pomocou Euklidovho algoritmu, myslíš tým iba prípad, keď jedna zo zátvoriek je deliteľná číslom 25?
BakyX | 11. 12. 2011 21:52:26
Je to asi nový Fermat.
BakyX | 11. 12. 2011 21:50:58
Kamarát riešil školské kolo a nestíhal, tak k 3. úlohe napísal, že tieto čísla sú nesúdeliteľné, čo ľahko overím pomocou Euklidovho algoritmu. Samozrejme to overiť nevedel a nemal časť zisťovať, či sa to dá...
Mark Daniel | 11. 12. 2011 20:59:12
BakyX: A to zadanie si si vymyslel sám alebo si ho niekde videl?
BakyX | 11. 12. 2011 17:25:05
Zmierme sa s tým, že to pre nejaké horibilne vysoké  možno neplatí, alebo je to nová "Veľká Fermatová veta" :D
možno neplatí, alebo je to nová "Veľká Fermatová veta" :D
Mark Daniel | 11. 12. 2011 12:09:52
Ano, je fakt blábol. Minimálne ten druhý príspevok. To je ozaj báchorka.
Miroslav Olšák | org | 11. 12. 2011 10:47:21
Aha! Skolni kolo. To mnohe vysvetluje, konkretne 1) kde se ta Bakyxova uloha vzala, 2) proc se snazis ji resit pres posledni cifru.
Ta uloha ze skolskeho kola se resi takto, ze?
+ skrytý text
Jenze, co nam z toho plyne pro Bakyxovu ulohu?
+ skrytý text
Ta uloha ze skolskeho kola se resi takto, ze?
+ skrytý text
Pro dost velka  uz bude
uz bude  prilis velke, aby to mohlo delit samotne
prilis velke, aby to mohlo delit samotne  nebo
nebo  . Proto uz by musely byt delitelne peti obe tyto zavorky. Staci se ovsem podivat na zbytky mocnin dvojky a trojky modulo peti (resp. posledni cifry):
. Proto uz by musely byt delitelne peti obe tyto zavorky. Staci se ovsem podivat na zbytky mocnin dvojky a trojky modulo peti (resp. posledni cifry):
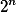 : 1 2 4 3 1
: 1 2 4 3 1
 : 1 3 4 2 1
: 1 3 4 2 1
Vidime, ze proti sobe nelicuji spravne zbytky, tedy nemohou byt delitelne peti obe zavorky.
Vidime, ze proti sobe nelicuji spravne zbytky, tedy nemohou byt delitelne peti obe zavorky.
Jenze, co nam z toho plyne pro Bakyxovu ulohu?
+ skrytý text
Ukazali jsme pouze, ze obe zavorky nejsou soucasne delitelne peti (delitelnost dvemi a peti se pres posledni cifru da). Nicmene co ostatni cisla? Napriklad nasobky 13, 17, 521, 769 mohou koncit na uplne jakoukoli cifru.
Anonym | 11. 12. 2011 00:06:32
Nechci přímo psát, že je to blábol, ale tudy cesta nevede.
Mark Daniel | 10. 12. 2011 23:45:18
Mirek: Teraz rozhodne neobhajujem moje riešenie, možno je to celé blbosť.
Iba k tej poznámke, čo sa dá usudzovať z poslednej cifry. Napríklad 3. úloha školského kola MO A sa dala v podstate celá vyriešiť cez to, aká cifra je na konci.
Iba k tej poznámke, čo sa dá usudzovať z poslednej cifry. Napríklad 3. úloha školského kola MO A sa dala v podstate celá vyriešiť cez to, aká cifra je na konci.
Mark Daniel | 10. 12. 2011 23:22:07
Ospravedlňujem sa po druhé, na konci som naozaj niečo prehliadol. Posledný odstavec je celý zlý, takže ešte raz:
Keď sa obe zátvorky končia číslicou 9:
+ skrytý text
Keď sa obe zátvorky končia číslicou 9:
+ skrytý text
Tak potom 2 na n-tú sa končí číslicou 8 a 3 na n-tú sa končí číslicou 7. Vieme, že (2 na n-tú)*(1,5 na n-tú)=(3 na n-tú). A vieme, že ak máme číslo, na ktorého konci je číslica 8 a chceme ho vynásobiť istým číslom A tak, aby výsledný súčin mal konci číslicu 7, tak potom A musí mať za desatinnou čiarkou číslo:......,1/(8/7). Pritom 1//(8/7) je číslo 0,875. A 1,5 na n-tú nikdy nie je číslo, ktoré sa takto končí. Aspoň si to myslím. Možno sa mýlim.
A ak sa prvá zátvorka končí číslicou 5 a druhá číslicou 1, tak 2 na n-tú sa končí číslicou 4 a 3 na n-tú číslicou 9. Teraz teda budeme násobiť číslo 2 na n-tú číslom takým číslom B, aby mal výsledný súčin na konci číslicu 9. To znamená, že číslo A má na konci hodnotu: 1/(4/9), čo je 2,25. Ale môže sa 1,5 na n-tú končiť hodnotou 2,25?
A ak sa prvá zátvorka končí číslicou 7 a druhá číslicou 3, tak 2 na n-tú sa končí číslicou 6 a 3 na n-tú číslicou 1. A opäť, ak chceme vynásobiť 2 na n-tú, tak aby vzniklo 3 na n-tú, musíme 2 na n-tú násobiť takým číslom C, aby C malo za desatinnou čiarkou hodnotu ...,1/(1/6). To znamená, že sa bude končiť takto: ....6,0. Ale 1,5 na n-tú sa nikdy takto nekončí.
A ak sa prvá zátvorka končí číslicou 5 a druhá číslicou 1, tak 2 na n-tú sa končí číslicou 4 a 3 na n-tú číslicou 9. Teraz teda budeme násobiť číslo 2 na n-tú číslom takým číslom B, aby mal výsledný súčin na konci číslicu 9. To znamená, že číslo A má na konci hodnotu: 1/(4/9), čo je 2,25. Ale môže sa 1,5 na n-tú končiť hodnotou 2,25?
A ak sa prvá zátvorka končí číslicou 7 a druhá číslicou 3, tak 2 na n-tú sa končí číslicou 6 a 3 na n-tú číslicou 1. A opäť, ak chceme vynásobiť 2 na n-tú, tak aby vzniklo 3 na n-tú, musíme 2 na n-tú násobiť takým číslom C, aby C malo za desatinnou čiarkou hodnotu ...,1/(1/6). To znamená, že sa bude končiť takto: ....6,0. Ale 1,5 na n-tú sa nikdy takto nekončí.
Miroslav Olšák | org | 10. 12. 2011 23:10:40
Cele jsem to necetl, (protoze to je desne dlouhe), ale obavam se, ze to nefunguje. Z posledni cifry se prece neda nic usuzovat (maximalne tak sudost a delitelnost peti). Ovsem uz vubec, jestli je cislo prvocislem nebo jestli jsou dve cisla nesoudelna. Taky z toho textu mam trochu pocit, ze aby cislo koncilo na jednicku, musi byt mocninou jedenactky.
Nebo jsem prehledl nejakou nosnou myslenku? Jak to vidi ostatni?
Nebo jsem prehledl nejakou nosnou myslenku? Jak to vidi ostatni?




