Miško | org | 7. 1. 2012 23:47:09
Štěpán:
+ skrytý text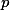 a
a 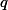 môžu mať na začiatku dokonca spoločné reálne korene ktoré nemôžeme úplne beztrestne pokrátiť, pretože úplne precízne napr.
môžu mať na začiatku dokonca spoločné reálne korene ktoré nemôžeme úplne beztrestne pokrátiť, pretože úplne precízne napr.  je iná funkcia ako
je iná funkcia ako 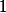 , pretože nie je definovaná v nule.
, pretože nie je definovaná v nule.
Ja som to tam nenapísal, ale bez ujmy na všeobecnosti môžeme predpokladať, že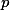 a
a 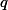 nemajú spoločné (komplexné) korene. Ak totiž majú, tak
nemajú spoločné (komplexné) korene. Ak totiž majú, tak

až na konečne veľa bodov, a to nám nevadí kvôli tomu, ako Kuba formuloval ten problém.
+ skrytý text
Ja som to tam nenapísal, ale bez ujmy na všeobecnosti môžeme predpokladať, že
až na konečne veľa bodov, a to nám nevadí kvôli tomu, ako Kuba formuloval ten problém.
Štěpán | 7. 1. 2012 16:50:28
Miško:
+ skrytý text
+ skrytý text
Myslím, že to co říkáš zcela neplatí. Protože podle mě mohou mít  a
a 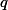 společné některé komplexní kořeny, ne? Ale nemělo by to snad moc změnit. Podle mě stačí udělat
společné některé komplexní kořeny, ne? Ale nemělo by to snad moc změnit. Podle mě stačí udělat  a
a  jako
jako  a
a  , kde
, kde  je polynom, který má komplexní kořeny společné v
je polynom, který má komplexní kořeny společné v  a
a 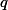 (budeme mít tedy polynomy nad komplexními čísly). Podobně vytvoříme
(budeme mít tedy polynomy nad komplexními čísly). Podobně vytvoříme  a
a  . Pak tvým postupem dokážeme
. Pak tvým postupem dokážeme  a
a  a tedy platí:
a tedy platí:
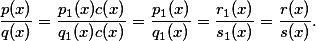
Miško | org | 6. 1. 2012 23:09:42
Ja si myslím, že to platí.
+ skrytý text
+ skrytý text
Nech pre nekonečne veľa  platí
platí

kde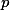 a
a 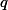 resp.
resp.  a
a  nemajú spoločný koreň. Potom
nemajú spoločný koreň. Potom  sa rovnajú v nekonečne veľa bodoch a sú to teda rovnaké polynómy.
sa rovnajú v nekonečne veľa bodoch a sú to teda rovnaké polynómy.
Tzn. tieto polynómy majú rovnaké korene. Ak je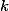 koreň polynómu
koreň polynómu  , tak potom to musí byť tiež koreň
, tak potom to musí byť tiež koreň  , pretože
, pretože 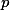 a
a 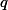 nemajú spoločný koreň. Podobne ak
nemajú spoločný koreň. Podobne ak  je koreň
je koreň  , potom musí byť aj koreňom
, potom musí byť aj koreňom  . Preto
. Preto  a
a  , hotovo.
, hotovo.
kde
Tzn. tieto polynómy majú rovnaké korene. Ak je
Kuba | 6. 1. 2012 22:06:13
Ten dotaz je asi dost hloupý a pravděpodobně bych na to byl schopen přijít po čase sám, ale teď trochu nestíhám a rada by se mi hodila. Je jasné (dokazovali jsme to i na tuším Pepově přednášce o polynomech), že když mají dva polynomy nad reálnými čísly nekonečně mnoho společných bodů, pak jsou totožné.
Dalo by se totéž tvrzení nějak (jakkoli) rozšířit na racionální funkce? (Nevyznám se přesně v termínech - myslím prostě podíl dvou polynomů.) Konkrétně bych rád věděl, jestli platí tvrzení: "Jestliže mají dvě lomené funkce nad reálnými čísly nekonečně mnoho společných bodů, pak mají společné všechny body až na konečně mnoho."
Těch "konečně mnoho" rozdílných bodů jsem tam dal kvůli nulovým bodům. Platí tohle tvrzení? Případně nějaké podobné? Díky
Dalo by se totéž tvrzení nějak (jakkoli) rozšířit na racionální funkce? (Nevyznám se přesně v termínech - myslím prostě podíl dvou polynomů.) Konkrétně bych rád věděl, jestli platí tvrzení: "Jestliže mají dvě lomené funkce nad reálnými čísly nekonečně mnoho společných bodů, pak mají společné všechny body až na konečně mnoho."
Těch "konečně mnoho" rozdílných bodů jsem tam dal kvůli nulovým bodům. Platí tohle tvrzení? Případně nějaké podobné? Díky
Vita | 3. 1. 2012 13:30:57
Zdravim z Indie! Po chvili cestovani jsem ted na konferenci, tak mam trochu casu na netu ;)
Ja si nemyslim, ze je ta teorie cisel tak tezka, jak tvrdite :) (Tohle je poprvy, co neco pisu v novym chatu, tak snad zvladnu to formatovani.)
+ skrytý text
Ja si nemyslim, ze je ta teorie cisel tak tezka, jak tvrdite :) (Tohle je poprvy, co neco pisu v novym chatu, tak snad zvladnu to formatovani.)
+ skrytý text
Jde o to najit n a p tak, aby  a
a  . A takovyhle ulohy se musi resit pouzitim primitivniho prvku! To je takovy cislo, ze jeho umocnovanim dostanu vsechny cisla modulo
. A takovyhle ulohy se musi resit pouzitim primitivniho prvku! To je takovy cislo, ze jeho umocnovanim dostanu vsechny cisla modulo  (az na nulu). A existuje dokonce modulo
(az na nulu). A existuje dokonce modulo  .
.
V tom, co napisu, bude spousta der, ale nejak tak to musi jit vyresit :)
Tak si zvolme tak, aby 3 bylo primitivni prvek. A at
tak, aby 3 bylo primitivni prvek. A at  , taky
, taky  . Pak muzu ty dve kongruence prepsat jako
. Pak muzu ty dve kongruence prepsat jako  a
a  (to presne plyne z definice primitivniho prvku). No a ted to jenom vyresit:
(to presne plyne z definice primitivniho prvku). No a ted to jenom vyresit:
Rychle spoctu, ze a odpovidajici
a odpovidajici  funguji.
funguji.
Takze jediny, co je potreba zjistit, je, jestli takovy existuje. Potrebujeme, aby 3 bylo primitivni prvek (to neni problem) a aby
existuje. Potrebujeme, aby 3 bylo primitivni prvek (to neni problem) a aby  . To rozhodne neni trivialni, ale na druhou stranu jsme taky to
. To rozhodne neni trivialni, ale na druhou stranu jsme taky to  mohli zvolit spoustou jinych zpusobu - a to by v tom byl cert, aby nejaky nefungoval! (Napr. ani neumime dokazat, ze je nekonecne mnoho prvocisel tvaru
mohli zvolit spoustou jinych zpusobu - a to by v tom byl cert, aby nejaky nefungoval! (Napr. ani neumime dokazat, ze je nekonecne mnoho prvocisel tvaru  - ale dost jiste jich nekonecne je.)
- ale dost jiste jich nekonecne je.)
Myslim, ze by takto mela jit vyresit kazda uloha podobnyho typu - budto v kongruencich mod p-1 bude videt, ze to nema reseni, nebo je casem najdu - to ale jenom pro konkretni situaci. Ze to fakt plati kdykoli, to asi bude beznadejne tezky otevreny problem.
V tom, co napisu, bude spousta der, ale nejak tak to musi jit vyresit :)
Tak si zvolme
Rychle spoctu, ze
Takze jediny, co je potreba zjistit, je, jestli takovy
Myslim, ze by takto mela jit vyresit kazda uloha podobnyho typu - budto v kongruencich mod p-1 bude videt, ze to nema reseni, nebo je casem najdu - to ale jenom pro konkretni situaci. Ze to fakt plati kdykoli, to asi bude beznadejne tezky otevreny problem.
miso z po | 28. 12. 2011 21:44:27
diki za text, vidi se mi viac popisany.
miso z PO | 28. 12. 2011 21:43:58
stacilo by resit toto, ja to fak neumim, jak to spravil?
http://forum.matweb.cz/viewtopic.php?id=38948
http://forum.matweb.cz/viewtopic.php?id=38948
Vejtek | 28. 12. 2011 19:16:45
Není tomu tak dlouho, co na MFF proběhla přednáška na téma funkcionální rovnice. Materiály k ní jsou ale stále k dispozici na adrese
http://www.karlin.mff.cuni.cz/olympiada/anota...
Úvod je však psaný poněkud stroze, takže je vhodnější spíše pro čerpání pokročilejších technik. Pokud si najdu více času, zkusím text trochu obohatit, ale kdo ví... třeba si to nechám na seriál [o:
http://www.karlin.mff.cuni.cz/olympiada/anota...
Úvod je však psaný poněkud stroze, takže je vhodnější spíše pro čerpání pokročilejších technik. Pokud si najdu více času, zkusím text trochu obohatit, ale kdo ví... třeba si to nechám na seriál [o:
Miso | 27. 12. 2011 10:15:19
Ano, ale sem se zastavil okolo ulohy 3, potom resim http://mks.mff.cuni.cz/common/show.php?title=...
a zastavil som sa pri cauchyho metode.
a zastavil som sa pri cauchyho metode.
Anonym | 26. 12. 2011 22:52:47
miso z presova: Jak tak koukám na tvé příspěvky na tom fóru, tak bych spíš doporučoval nejprve pochopit základní věci z matematiky. Zjistit si, co je to funkce, co je to univerzální kvantifikátor a podobně. Přečetl jsi si povídání ke čtvrté sérii? http://mks.mff.cuni.cz/common/show.php?title=...
miso z presova | 26. 12. 2011 22:17:56
kto by mi mohol pomôcť ? s tymy funkcionalnymi rovnicami? http://forum.matweb.cz/viewforum.php?id=26
Kenny | 23. 12. 2011 20:01:25
Mirek si po nocích dělí velká čísla :)
Miroslav Olšák | org | 23. 12. 2011 12:23:50
Jeste k Bakyxove teorii cisel: spolecny delitel vetsi nez 1 by musel byt vetsi nez 107839350007. A vzdavam to, treba to vazne plati.
Kenny | 18. 12. 2011 19:45:07
Pappova věta není moc známá a v olympiádách se běžně nepoužívá (sám jsem ji v úloze použil možná poprvé).
http://mathworld.wolfram.com/PappussHexagonTh...
Její důkaz pomocí elementárních metod dá docela zabrat, nicméně v tomhle případě, kdy jde o rovnoběžné přímky se zjednoduší na pár podobností.
http://mathworld.wolfram.com/PappussHexagonTh...
Její důkaz pomocí elementárních metod dá docela zabrat, nicméně v tomhle případě, kdy jde o rovnoběžné přímky se zjednoduší na pár podobností.
BakyX | 18. 12. 2011 17:28:16
Ďakujem za odpoveď. Nechápem, ako môže byť niekto taký good ako vy..Pripíšem na zoznam vecí čo nechápem.
K tým riešeniam. To Kennyho i) nechápem, nepoznám ani Pappovu vetu. Nechápem ani to Pepove cez harmóniu. Nevadí. Ďakujem
K tým riešeniam. To Kennyho i) nechápem, nepoznám ani Pappovu vetu. Nechápem ani to Pepove cez harmóniu. Nevadí. Ďakujem
Kenny | 18. 12. 2011 15:51:22
No jo no, řešil jsem to ve spěchu, tak jsem to stihl jen rozbít na "známá" tvrzení. Pochopí mé neelementární řešení i někdo jiný než Pepa? :)
Josef Tkadlec | 18. 12. 2011 12:36:34
Tak to Kennyho neelementární řešení je fakt pařba :D.
Podle mě úloha stojí na následujícím pozorování:
+ skrytý text
S tím už není problém úlohu spočítat (ala Kenny):
+ skrytý text
A nebo s trochou harmonického skillu dodělat synteticky:
+ skrytý text
Podle mě úloha stojí na následujícím pozorování:
+ skrytý text
BÚNO 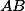 vodorovně. Pak body
vodorovně. Pak body  ,
, 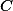 a
a  jsou všechny stejně vysoko.
jsou všechny stejně vysoko.
Tohle je lehké, když už člověk ví, že to chce dokázat. Důvod třeba:
+ skrytý text
Tohle je lehké, když už člověk ví, že to chce dokázat. Důvod třeba:
+ skrytý text
Stačí, že  . Jelikož
. Jelikož  je na
je na 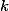 "vpravo", je ze stejnolehlosti
"vpravo", je ze stejnolehlosti 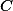 na
na  "vlevo".
"vlevo".
S tím už není problém úlohu spočítat (ala Kenny):
+ skrytý text
Umíme říct, jak moc je  od výšky "nalevo" a
od výšky "nalevo" a  napravo, takže umíme říct, jak "vysoko"
napravo, takže umíme říct, jak "vysoko"  tu výšku protne. Nemůže to nevyjít :).
tu výšku protne. Nemůže to nevyjít :).
Konkrétně: Z úseků k patám výšek a podobnosti máme a samozřejmě
a samozřejmě  . Poměr vychází
. Poměr vychází 
 symetricky, takže hotovo.
symetricky, takže hotovo.
Konkrétně: Z úseků k patám výšek a podobnosti máme
A nebo s trochou harmonického skillu dodělat synteticky:
+ skrytý text
Výška  protne kružnici
protne kružnici  "vpravo" (označme průsečík
"vpravo" (označme průsečík 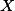 ). Harmonickou čtveřici
). Harmonickou čtveřici  promítneme z
promítneme z  na přímku
na přímku 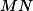 . Bod
. Bod  se zobrazí do průsečíku
se zobrazí do průsečíku 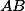 a
a 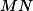 , takže
, takže  se zobrazí do průsečíku
se zobrazí do průsečíku 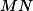 a výšky z
a výšky z 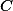 .
.
Kenny | 18. 12. 2011 11:36:16
Ahoj,
tak mám dvě řešení, ovšem ani jedno není zcela uspokojivé.
i) Syntetické ale neelementární:
+ skrytý text
ii) Počítací
+ skrytý text
Zvládne někdo rozluštit aspoň jedno moje řešení? Nebo najít lepší?
tak mám dvě řešení, ovšem ani jedno není zcela uspokojivé.
i) Syntetické ale neelementární:
+ skrytý text
Velmi hrubá kostra:
0) + skrytý text
1)+ skrytý text
2)+ skrytý text
3) + skrytý text
0) + skrytý text
Body 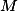 ,
, 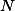 ,
, 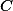 jsou body, v nichž se stran dotýká vepsaná kružnice
jsou body, v nichž se stran dotýká vepsaná kružnice  , kde
, kde  je střed
je střed 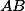
1)+ skrytý text
Pappova věta
2)+ skrytý text
Pokud paty dvou cevián leží stejně "vysoko", ty ceviány se protínají na těžnici.
3) + skrytý text
Známé tvrzení, že těžnice protíná spojnici bodů dotyku s vepsanou "nad" Ičkem
ii) Počítací
+ skrytý text
Ověřím Cevovu větu. Vše vyjádřím pomocí prvků trojúhelníka. V následujícím pořadí:
1) + skrytý text
2) + skrytý text
3) + skrytý text
4)+ skrytý text
1) + skrytý text
Úseky, na něž výšky dělí obvod trojúhelníka
2) + skrytý text
Z podobností vyjádřím poloměry obou kružnic. ( )
)
3) + skrytý text
Z dalších podobností vyjádřím, v jaké poměru jsem rozdělil strany 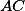 a
a 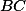 .
.
4)+ skrytý text
Dosadím, spočítám
Zvládne někdo rozluštit aspoň jedno moje řešení? Nebo najít lepší?
BakyX | 17. 12. 2011 22:03:34
Zdravím. Mohol by mi prosím niekto poradiť s touto pre mňa nezvládnuteľnou úlohou (vám odborníkom to zaberie tak 3 minúty). Ďakujem.
+ skrytý text
+ skrytý text
Je daný ostrouhlý trojuholník 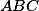 . Uvažujme kružnice
. Uvažujme kružnice 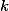 zostrojenú nad priemerom
zostrojenú nad priemerom 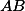 . Označme
. Označme  priesečníky
priesečníky 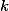 s úsečkami
s úsečkami  . Uvažujme kružnicu
. Uvažujme kružnicu 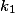 (respektíve
(respektíve 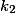 ), ktorá prechádza bodom
), ktorá prechádza bodom 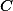 a dotýka sa kružnice
a dotýka sa kružnice 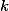 v bode
v bode 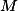 (respektíve
(respektíve 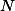 ). Stredy týchto kružníc označme
). Stredy týchto kružníc označme  . Označme
. Označme 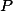 priesečník priamok
priesečník priamok  . Dokážte, že priamka
. Dokážte, že priamka  je výška trojuholníka
je výška trojuholníka 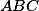 .
.
Josef Tkadlec | 17. 12. 2011 13:24:36
Na podnět Mirka: čtverce o úlohu zpátky se neměly překrývat, jinak je to z hlavy už trochu těžší (je tam nějaké počítání). Jelikož už máme další úlohu, doplním k tamté pro úplnost metodu, jak se dá na výsledek pohodlně přijít.
+ skrytý text
Olin: To jsi asi na minulém sousu nebyl na Martinině přednášce o rozkladech ;) (v knihovně na http://mks.mff.cuni.cz/library/library.php?ca...).
+ skrytý text
Úhlopříčky 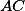 a
a  jsou rovnoběžné, takže obsah trojúhelníku
jsou rovnoběžné, takže obsah trojúhelníku  je stejný jako obsah trojúhelníku
je stejný jako obsah trojúhelníku  , což je půlka prvního čtverce. Velikost druhého čtverce nerozhoduje.
, což je půlka prvního čtverce. Velikost druhého čtverce nerozhoduje.
Olin: To jsi asi na minulém sousu nebyl na Martinině přednášce o rozkladech ;) (v knihovně na http://mks.mff.cuni.cz/library/library.php?ca...).





