Tonda | 23. 2. 2012 17:26:55
Čau,
potřebuju pomoc s jedním příkladem: Máme kružnici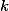 se středem
se středem 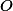 a postupně body
a postupně body  tak, aby
tak, aby  byl rovnostranný trojúhelník. Osy úseček
byl rovnostranný trojúhelník. Osy úseček  a
a  se protínají v
se protínají v  a protnou kružnici
a protnou kružnici 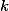 postupně v bodech
postupně v bodech  leží mezi
leží mezi  .
. 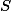 je průsečík přímek
je průsečík přímek  . Dokažte, že
. Dokažte, že  prochází středem trojúhelníka
prochází středem trojúhelníka  .
.
Předem děkuju za pomoc
potřebuju pomoc s jedním příkladem: Máme kružnici
Předem děkuju za pomoc
Mark Daniel | 22. 2. 2012 23:52:36
Informáciu som získal.
Mark Daniel | 21. 2. 2012 23:44:27
Dobrý deň,
Ako je možné vypočítať pod akým uhlom v konkrétnom bode smeruje krivka grafu vzhľadom na x-ovú os?
Ďakujem
Ako je možné vypočítať pod akým uhlom v konkrétnom bode smeruje krivka grafu vzhľadom na x-ovú os?
Ďakujem
Josef Tkadlec | 21. 2. 2012 23:39:10
Tonda: No už tomu chybí jenom krůček
Jinak tu letní školu můžu jen doporučit. Loni se konala v Německu a rozhodně stála za to.
Jinak tu letní školu můžu jen doporučit. Loni se konala v Německu a rozhodně stála za to.
Tonda | 21. 2. 2012 13:22:44
Cau,
k Solitairu
+ skrytý text
Dále se již odstartovalo přihlašování na letní matematickou školu ve Francii (termín 20 - 29 srpna), což je podle mě skvělá příležitost si procvičovat angličtinu a matematiku. Více na http://www.issmys.eu/
k Solitairu
+ skrytý text
Solitaire (neúplné řešení)
1) V každém tahu, kde pohybujeme tlustou figurkou, se jedna souřadnice tlusté figurky změní o dva, tzn. jeho parity souřadnic se nezmění. Dostaneme tak množinu 8 políček, kde může tlustá figurka být
2) Přiřadíme každému políčku po rovnoměrně po řádku a sloupci postupně hodnoty a,b,-a-b a snadno zjistíme, že po každém tahu se součet hodnot všech políček, na kterých jsou figurky změní o 2a, 2b nebo -2a, 2b. Tzn. zkoumáme-li součet všech políček s figurkami a podíváme-li se na koeficienty u a,b, snadno zjistíme, že parita těchto koeficientů se nezmění. Přiřadíme prvnímu políčku prvního řádku čísla a, pak hledaný součet je b. Na konci máme jen jedno políčko, a proto to políčko musí mít hodnotu b. Dostaneme tak množinu 11 políček.
Vezmeme-li průnik dvou zmíněných množin, zůstanou nám jen 4 hodnoty, které musíme ale ještě ověřit.
1) V každém tahu, kde pohybujeme tlustou figurkou, se jedna souřadnice tlusté figurky změní o dva, tzn. jeho parity souřadnic se nezmění. Dostaneme tak množinu 8 políček, kde může tlustá figurka být
2) Přiřadíme každému políčku po rovnoměrně po řádku a sloupci postupně hodnoty a,b,-a-b a snadno zjistíme, že po každém tahu se součet hodnot všech políček, na kterých jsou figurky změní o 2a, 2b nebo -2a, 2b. Tzn. zkoumáme-li součet všech políček s figurkami a podíváme-li se na koeficienty u a,b, snadno zjistíme, že parita těchto koeficientů se nezmění. Přiřadíme prvnímu políčku prvního řádku čísla a, pak hledaný součet je b. Na konci máme jen jedno políčko, a proto to políčko musí mít hodnotu b. Dostaneme tak množinu 11 políček.
Vezmeme-li průnik dvou zmíněných množin, zůstanou nám jen 4 hodnoty, které musíme ale ještě ověřit.
Dále se již odstartovalo přihlašování na letní matematickou školu ve Francii (termín 20 - 29 srpna), což je podle mě skvělá příležitost si procvičovat angličtinu a matematiku. Více na http://www.issmys.eu/
Josef Tkadlec | 20. 2. 2012 21:40:20
Znáte hru Solitaire? Ne tu karetní, ale tu, kde se na hracím plánu přeskakují a odebírají figurky. Úkolem bývá popřeskákat figurky tak, aby zbyla jediná(kdyžtak wiki: peg solitaire). Našel jsem jednu vtipnou variantu téhle hry.
Na začátku vypadá hrací deska jako na obrázku http://atrey.karlin.mff.cuni.cz/~pepat/PraSe/... (tj. obsahuje jediné prázdné políčko skoro vlevo nahoře a jednu tlustou figurku). Ví se, že se figurky dají přeskákat tak, aby zbyla jediná, a to ta tlustá. Otázka zní, na kterých všech políčkách může ta figurka zbýt.
Na začátku vypadá hrací deska jako na obrázku http://atrey.karlin.mff.cuni.cz/~pepat/PraSe/... (tj. obsahuje jediné prázdné políčko skoro vlevo nahoře a jednu tlustou figurku). Ví se, že se figurky dají přeskákat tak, aby zbyla jediná, a to ta tlustá. Otázka zní, na kterých všech políčkách může ta figurka zbýt.
BakyX | 3. 2. 2012 16:09:46
Pavel: Nabudúce zadanie príkladu nebudem skrývať.
Ďakujem za radu k príkladu. Na toto by som fakt neprišiel.
Ďakujem za radu k príkladu. Na toto by som fakt neprišiel.
Pavel Šalom | 1. 2. 2012 10:50:02
Cau,
na Talnetu se se zpozdenim objevil zaznam prednasky o Geometrickych zobrazenich, ktera slouzi jako doplneni serialu. Odkaz najdete na http://www.talnet.cz/cafe-talnet
na Talnetu se se zpozdenim objevil zaznam prednasky o Geometrickych zobrazenich, ktera slouzi jako doplneni serialu. Odkaz najdete na http://www.talnet.cz/cafe-talnet
Pavel Šalom | 29. 1. 2012 17:35:59
Jinak k te maximalizacni uloze:
hint:
+ skrytý text
Verim, ze pokud je hint pochopitelny, melo by byt reseni tak nejak videt. Nicmene navod jak to sepsat, by mohl byt napriklad:
+ skrytý text
hint:
+ skrytý text
Co mam udelat, aby me zvetseni souctu  o
o  vyslo "co nejlevneji"?
vyslo "co nejlevneji"?
Verim, ze pokud je hint pochopitelny, melo by byt reseni tak nejak videt. Nicmene navod jak to sepsat, by mohl byt napriklad:
+ skrytý text
Uvazme maximalni soucet  a necht v nem nejvetsi je
a necht v nem nejvetsi je  a nejmensi
a nejmensi  . Chceme ukazat, ze souctu
. Chceme ukazat, ze souctu  umime dosahnout a pritom splnit
umime dosahnout a pritom splnit  . Pokud by tomu tak nebylo, uvazime
. Pokud by tomu tak nebylo, uvazime  -tici, ve které zmenime pouze
-tici, ve které zmenime pouze  na
na  a
a  na
na  . Tim zmensime soucet tretich mocnin (rozmyslet) a nezmenime soucet
. Tim zmensime soucet tretich mocnin (rozmyslet) a nezmenime soucet  .
.
Pak staci rict neco takoveho, ze nemuzeme vzit same dvojky, to by byl soucet tretich mocnin , takze umime maximalni soucet vyrobit jen z jednicek a dvojek.
, takze umime maximalni soucet vyrobit jen z jednicek a dvojek.
Vysledek mi pak vysel:
+ skrytý text .
.
Pak staci rict neco takoveho, ze nemuzeme vzit same dvojky, to by byl soucet tretich mocnin
Vysledek mi pak vysel:
+ skrytý text
Pavel Šalom | 29. 1. 2012 16:46:12
Cau, chtel bych se primluvit za to, aby se zadani uloh neskryvalo. Prijde mi naprosto v poradku, aby v tomto chatu zadani videli vsichni.
BakyX | 29. 1. 2012 12:11:18
Vejtek, |: + skrytý text
Skúšal som to a myslel som si, že výsledok je rovný celej časti toho maxima, ale nie je.
Anonym | 29. 1. 2012 00:42:24
+ skrytý text
Proč tam tahat Höldera? Na to snad stačí normální nerovnost mezi aritmetickým a kubickým průměrem.
Vejtek | 28. 1. 2012 23:57:13
BakyX:+ skrytý text
Co zkusit Höldera pro (3,3/2)? Ten dá aspoň horní odhad..
BakyX | 28. 1. 2012 22:26:24
Rado: Ďakujem :)
Potreboval by som poradiť s ešte jednou úlohou. Ďakujem
+ skrytý text
Potreboval by som poradiť s ešte jednou úlohou. Ďakujem
+ skrytý text
Je dané prirodzené číslo  . Nech
. Nech  sú nezáporné celé čísla spĺňajúce
sú nezáporné celé čísla spĺňajúce

Nájdi maximálnu hodnotu súčtu
Nájdi maximálnu hodnotu súčtu
Rado | 28. 1. 2012 19:22:27
BakyX: asi mám elementárnější řešení :
+ skrytý text
Btw:email
+ skrytý text
Rozděl si všechny čísla do n množin podle modula n. Protože prvočísel je nekonečno, v alespoň v jedné množině je nekonečně prvočísel. Zbytek už zvládneš sám ;)
Btw:email
BakyX | 28. 1. 2012 17:25:08
Rado: To som si všimol, že je. Btw. Nedáš mi prosím kontakt na teba ?
Rado | 28. 1. 2012 16:22:02
BakyX: je to speciální případ + skrytý text
Dirichletova věta o prvočíslech (http://mathworld.wolfram.com/DirichletsTheore...
, ale to mi příjde jako trochu moc brutální kalibr. Klasickými středoškolskými metodami fakt netuším.BakyX | 28. 1. 2012 15:05:26
Dobrý deň. Poradíte mi prosím, ako vyriešiť tento príklad ? Ďakujem
+ skrytý text
+ skrytý text
Je dané prirodzené číslo  . Dokáž, že existuje prvočíslo
. Dokáž, že existuje prvočíslo  také, že existuje nekonečne veľa prvočísel v tvare
také, že existuje nekonečne veľa prvočísel v tvare 
Miroslav Olšák | org | 23. 1. 2012 22:26:07
Nabizim k pohrani geogebri soubory tykajici se serialu (tedy i nedavno probehle prednasky):
http://www.geogebratube.org/user/profile/id/1...
Zaznam te prednasky se snad casem objevi na
http://www.talnet.cz/cafe-talnet
http://www.geogebratube.org/user/profile/id/1...
Zaznam te prednasky se snad casem objevi na
http://www.talnet.cz/cafe-talnet
Vejtek | 19. 1. 2012 20:00:27
Naznačit může [o:
Problém byl v tom, že zadání nám nic neříká o případu , přestože
, přestože 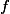 je v tomto bodě definována. Většina řešitelů si označila
je v tomto bodě definována. Většina řešitelů si označila  pro
pro  a pak tvrdila, že platí
a pak tvrdila, že platí  . Ale to nemusí vůbec platit! První rovnost je ještě vpořádku, platí pro
. Ale to nemusí vůbec platit! První rovnost je ještě vpořádku, platí pro  , ale o druhé rovnosti můžeme obecně těžko soudit, jelikož platí pouze pouze pro ta
, ale o druhé rovnosti můžeme obecně těžko soudit, jelikož platí pouze pouze pro ta  , kde
, kde  .
.
Správně se s tím popral jen Tonda, který definoval pro všechna
pro všechna  . Tento krok nám zaručí platnost výše popsané formule všude, neboť o
. Tento krok nám zaručí platnost výše popsané formule všude, neboť o 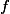 předpokládáme, že existuje. Chyby se však ani on nevyvaroval, neboť při určování pevných bodů zapomněl na hodnotu
předpokládáme, že existuje. Chyby se však ani on nevyvaroval, neboť při určování pevných bodů zapomněl na hodnotu  ,
,
o které víme pramálo. Schválně: Jak je to s fixpunkty funkce

v závislosti na ?
?
Problém byl v tom, že zadání nám nic neříká o případu
Správně se s tím popral jen Tonda, který definoval
o které víme pramálo. Schválně: Jak je to s fixpunkty funkce
v závislosti na




