Štěpán | 13. 3. 2012 21:12:16
Nechcete dát někdo hint k osmičce? Seděl jsem nad tou úlohou pekelně dlouho a nemohl jsem to rozlousknout :P
Tonda | 12. 3. 2012 18:07:08
Poprosím orgy o smazání tří mých nesmyslých dolních příspěvků.
Hint ke konstrukční úloze:
+ skrytý text
Hint ke konstrukční úloze:
+ skrytý text
Chceme nakreslit přímky, ale kružítko umí dělat jen kružnice. Jenže umíme hravě převést přímky na kružnice a naopak
Tonda | 7. 3. 2012 23:42:08
Ahoj,
mám jednu zajímavou konstrukční úlohu: máte-li 3 body v rovině, najděte pomocí kružítka střed kružnice opsané tří zadaných bodů.
Můžete pak zkusit i další level: jsou dány 4 body A,B,C,D rovině, najděte pomocí kružítka průsečík přímek AB a CD.
mám jednu zajímavou konstrukční úlohu: máte-li 3 body v rovině, najděte pomocí kružítka střed kružnice opsané tří zadaných bodů.
Můžete pak zkusit i další level: jsou dány 4 body A,B,C,D rovině, najděte pomocí kružítka průsečík přímek AB a CD.
Miroslav Olšák | org | 7. 3. 2012 20:11:36
Misto kruznice opsane  pouzij kruznici prochazejici
pouzij kruznici prochazejici 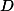 , ktera se dotyka primky
, ktera se dotyka primky 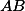 v
v 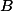 .
.
Rado | 7. 3. 2012 19:29:44
Ahoj. Dneska jsem si řešil jednu úlohu a napadlo mně: střed spirální podobnosti zobrazující 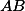 na
na 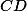 se zkonstruuje tak, že vezmeme průsečík
se zkonstruuje tak, že vezmeme průsečík 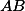 a
a 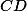 (třeba
(třeba 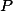 ) a je to druhý průsečík kružnic opsaných
) a je to druhý průsečík kružnic opsaných  a
a  , mám pravdu? Ale co když je oním průsečíkem
, mám pravdu? Ale co když je oním průsečíkem 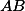 a
a 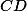 třeba
třeba 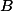 ? Zkoušel jsem to nějak vyřešit, ale protože geometrie mi totálně nejde, samozřejmě jsem na nic nepřišel ;)
? Zkoušel jsem to nějak vyřešit, ale protože geometrie mi totálně nejde, samozřejmě jsem na nic nepřišel ;)
Miroslav Olšák | org | 5. 3. 2012 00:21:40
Souhlasim, bylo ale treba si z toho, co tonda napsal, vyzobat to, co plati. Predevsim me matlo, ze by mel byt R druhym prusecikem kruznic.
BakyX | 4. 3. 2012 23:52:46
Mirek: Milé vyznanie od vás.
Ja som si to domyslel takto:
Rovnobežky sú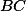 a
a 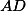 . V rovnoľahlosti, ktorá zobrazuje úsečku
. V rovnoľahlosti, ktorá zobrazuje úsečku 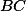 do úsečky
do úsečky  zobrazíme bod
zobrazíme bod 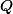 do bodu
do bodu  . Potom body
. Potom body  ležia na kružnici a ďalej je to zrejmé.
ležia na kružnici a ďalej je to zrejmé.
Ja som si to domyslel takto:
Rovnobežky sú
Miroslav Olšák | org | 4. 3. 2012 22:38:14
Dovolim si trochu poopravit Tondovo reseni. I s nim mi totiz chvili trvalo na to prijit.
+ skrytý text
Bylo to tak mysleno, ze?
Obdivuji Bakyxe, ze si precte, co Tonda napise, a rovnou v tom vidi spravne reseni. Musi to byt genius :)
+ skrytý text
ad 2) Zobrazime Q ...
ad 3) ... prusecik kruznice opsane BCQ s primkou QP
ad 3) ... prusecik kruznice opsane BCQ s primkou QP
Bylo to tak mysleno, ze?
Obdivuji Bakyxe, ze si precte, co Tonda napise, a rovnou v tom vidi spravne reseni. Musi to byt genius :)
Tonda Le | 4. 3. 2012 20:59:16
Asi tě musím zklamat, ale jsem na tohle nepřišel :D Jsem tuto úlohu jenom znal
Ale myslím si, že génius být nemusíš, protože ten krok není úplně nepřirozený. Máme-li lichoběžník a v něm už předem označený průsečík úhlopříček, tak stejnolehlost je jedna dobrá možnost, jak tyto informace použít.
Ale myslím si, že génius být nemusíš, protože ten krok není úplně nepřirozený. Máme-li lichoběžník a v něm už předem označený průsečík úhlopříček, tak stejnolehlost je jedna dobrá možnost, jak tyto informace použít.
BakyX | 4. 3. 2012 20:35:53
Ďakujem Tonda.
To je geniálna myšlienka. Ako sa na niečo takéto prísť ? Musím byť génius ako ty ?
To je geniálna myšlienka. Ako sa na niečo takéto prísť ? Musím byť génius ako ty ?
Tonda Le | 4. 3. 2012 18:06:47
Ahoj,
tato úloha je G3 z shortlistu 2007, což je poměrně těžká
1) Bod P je střed stejnolehlosti S zobrazující AB na CD
2) Zobrazíme bod P podle stejnolehlosti S na bod R
3) Bod R je druhý průsečík kružnic opsaných trojúhelníkům ADQ, BCQ a zbytek už je přímočarý
tato úloha je G3 z shortlistu 2007, což je poměrně těžká
1) Bod P je střed stejnolehlosti S zobrazující AB na CD
2) Zobrazíme bod P podle stejnolehlosti S na bod R
3) Bod R je druhý průsečík kružnic opsaných trojúhelníkům ADQ, BCQ a zbytek už je přímočarý
BakyX | 2. 3. 2012 21:51:37
Pepa T. Ďakujem. K návodu:
+ skrytý text
Nedal by mi niekto prosím hint k tejto úlohe ? Neviem sa vôbec pohnúť. Ďakujem.
Uhlopriečky lichobežníka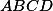 sa pretínajú v bode
sa pretínajú v bode 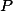 . Bod
. Bod 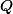 leží mezi rovnobežkami
leží mezi rovnobežkami 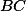 a
a 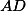 tak, že
tak, že  a priamka
a priamka 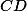 oddeľuje body
oddeľuje body 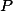 a
a 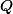 . Dokážte, že
. Dokážte, že  .
.
+ skrytý text
Mne v GeoGebre nevychádza, že vždy nastáva rovnosť.
Nedal by mi niekto prosím hint k tejto úlohe ? Neviem sa vôbec pohnúť. Ďakujem.
Uhlopriečky lichobežníka
Josef Tkadlec | 29. 2. 2012 22:04:40
Ahoj,
ano, dá. Hint: + skrytý text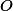 může být zcela libovolný bod v trojúhelníku.
může být zcela libovolný bod v trojúhelníku.
Návod:
+ skrytý text
ano, dá. Hint: + skrytý text
Návod:
+ skrytý text
Pro AGčko by stačilo, kdyby bylo

Ve skutečnosti nastává vždy rovnost (obsahy).
Ve skutečnosti nastává vždy rovnost (obsahy).
BakyX | 29. 2. 2012 18:38:24
Dobrý deň. Poradili by ste mi prosím, ako dokázať túto geometrickú nerovnosť ? Dá sa to bez goniometrie ? Ďakujem.
Označme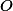 stred kružnice opísanej ostrouhlému trojuholníku
stred kružnice opísanej ostrouhlému trojuholníku 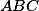 . Ďalej označme
. Ďalej označme  priesečníky priamok
priesečníky priamok  s úsečkami
s úsečkami  . Dokáž nerovnosť:
. Dokáž nerovnosť:

Označme
Kenny | 27. 2. 2012 14:26:06
Pěkně Mirku!
Takhle je to dobře jasný!
Takhle je to dobře jasný!
Miroslav Olšák | org | 27. 2. 2012 01:45:04
Kenny by úlohy jenom mlátil, mám lepší řešení.
+ skrytý text
+ skrytý text
Kenny | 26. 2. 2012 17:48:49
Úlohu lze docela jednoduše řešit ošklivě...
+ skrytý text
Pěkně to zatím neumím.
+ skrytý text
...výpočtem pomocí komplexních čísel.
Počátek dáme do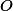 , kružnici jednotkovou a na ní tři rovnostranné trojúhelníky
, kružnici jednotkovou a na ní tři rovnostranné trojúhelníky  . Souřadnice středu trojúhelníka určíme snadno a zbývá nám tak dvakrát určit průsečík dvojice přímek a pak ověřit, že tři body leží v přímce.
. Souřadnice středu trojúhelníka určíme snadno a zbývá nám tak dvakrát určit průsečík dvojice přímek a pak ověřit, že tři body leží v přímce.
Výpočet na 10 minut...
Jelikož tipuju, že schopnost dopočítat se, na celostátku oddělí úspěšné od neúspěšných, vypisuji soutěž.
Kdo mi na mail pošle jako první (správný) výpočet, získává ode mne pivo (18+) nebo čokoládu (jinak).
Počátek dáme do
Výpočet na 10 minut...
Jelikož tipuju, že schopnost dopočítat se, na celostátku oddělí úspěšné od neúspěšných, vypisuji soutěž.
Kdo mi na mail pošle jako první (správný) výpočet, získává ode mne pivo (18+) nebo čokoládu (jinak).
Pěkně to zatím neumím.
Miroslav Olšák | org | 23. 2. 2012 20:58:04
Sice se mi to ted nechce resit (asi to bude fakt tezke, kdyz to nedal tonda), ale v geogebre mi to vyslo. A aby ostatni nemuseli lustit zadani:
http://www.geogebratube.org/material/show/id/...
http://www.geogebratube.org/material/show/id/...
Tonda | 23. 2. 2012 18:44:52
Kenny: Ahoj,
A,B,C,D leží v tomto pořadí. Pokud bereme A,D v horní polovině té kružice a B,C v té spodní polovině, pak U chceme, aby bylo nahoře a X,Y dole. Doufám, že to už je srozumitelnější. Přišel jsem na tenhle výsledek během řešení jedné úlohy z MOP 1996.
A,B,C,D leží v tomto pořadí. Pokud bereme A,D v horní polovině té kružice a B,C v té spodní polovině, pak U chceme, aby bylo nahoře a X,Y dole. Doufám, že to už je srozumitelnější. Přišel jsem na tenhle výsledek během řešení jedné úlohy z MOP 1996.
Kenny | 23. 2. 2012 18:31:53
Ahoj,
nerozumím úplně dobře zadání. Body leží na
leží na 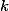 nebo úplně libovolně? Taky mi není jasné, které průsečíky os úseček
nebo úplně libovolně? Taky mi není jasné, které průsečíky os úseček  a
a  s
s 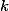 mám brát. Zkrátka neumím donutit geogebru, aby to v ní vyšlo :)
mám brát. Zkrátka neumím donutit geogebru, aby to v ní vyšlo :)
nerozumím úplně dobře zadání. Body





