πtr | org | 7. 4. 2012 16:18:39
Tondo: Termín je v utorok, pretože v pondelok je štátny sviatok - Velikonoce
Tonda | 7. 4. 2012 13:24:12
+ skrytý text
Pozn.: Proč termín na 3.sérii je v úterý?
BÚNO  a že obě jsou lichá prvočísla (to vyřešíme pak)
a že obě jsou lichá prvočísla (to vyřešíme pak)
Tvrzení (jednoduché): všechny prvočíselné dělitele čísla jsou buď 2 nebo prvočísla tvaru
jsou buď 2 nebo prvočísla tvaru  .
.
Nyní uvažujme lichá prvočísla , která dělí
, která dělí  a jsou menší než
a jsou menší než  . Taková prvočísla také dělí
. Taková prvočísla také dělí  a jsou menší než
a jsou menší než 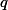 .
.



 má tvar
má tvar  , a proto
, a proto  může být jedině
může být jedině  , ale snadno zjistíme, že
, ale snadno zjistíme, že  nedělí
nedělí  , tzn. taková prvočísla
, tzn. taková prvočísla  neexistují, tzn.
neexistují, tzn.  je složené jen ze
je složené jen ze 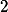 (jen jednou, rozmyslete si) a prvočísel větších než
(jen jednou, rozmyslete si) a prvočísel větších než  (také jen jednou, rozmyslete si).
(také jen jednou, rozmyslete si).
 má tedy tvar
má tedy tvar  , kde
, kde  je prvočíslo.
je prvočíslo.
 , a proto
, a proto  . Snadno vyloučíme hodnoty
. Snadno vyloučíme hodnoty  , tzn.
, tzn. 

 a
a  dává zbytek
dává zbytek 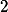 po dělení
po dělení 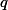 , a proto
, a proto  dává zbytek
dává zbytek  po dělení
po dělení 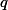 , a proto
, a proto  dává zbytek
dává zbytek  nebo
nebo  po dělení
po dělení 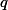 , nyní by to mělo být lehké.
, nyní by to mělo být lehké.
Případ když jedno prvočíslo je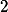 , pak jediné řešení bude
, pak jediné řešení bude 
Tvrzení (jednoduché): všechny prvočíselné dělitele čísla
Nyní uvažujme lichá prvočísla
Případ když jedno prvočíslo je
Pozn.: Proč termín na 3.sérii je v úterý?
BakyX | 6. 4. 2012 23:13:24
Dobrý deň. Mohol by mi prosím niekto poradiť, ako vyriešiť úlohu číslo 39 z http://mks.mff.cuni.cz/common/show.php?title=... ?
Nemám najmenšie tušenie, čo s tým. Neviem to vyriešiť ani pre .
.
Ďakujem.
Nemám najmenšie tušenie, čo s tým. Neviem to vyriešiť ani pre
Ďakujem.
BakyX | 5. 4. 2012 16:22:13
Ďakujem za super pomoc :)
+ skrytý text
+ skrytý text
Toto je dosť drsný trik. Snáď sa také raz naučím..
Josef Tkadlec | 5. 4. 2012 15:53:13
+ skrytý text
1) Stačí dokázat  .
.
2) Čáry ,
,  jsou isogonální v úhlu
jsou isogonální v úhlu  a podobně s
a podobně s 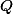 (viz druhý díl seriálu ;)).
(viz druhý díl seriálu ;)).
2) Čáry
BakyX | 5. 4. 2012 15:15:52
Dobrý deň. Mohol by mi niekto prosím poradiť, ako vyriešiť úlohu číslo 4 z http://skmo.sk/dokument.php?id=402 ? Stačí hint. Ďakujem.
BakyX | 31. 3. 2012 22:53:15
Ďakujem za pomoc.
+ skrytý text
+ skrytý text
Tie tvary: Číslo  má požadovanú vlasnosť práve vtedy, keď je
má požadovanú vlasnosť práve vtedy, keď je  štvorec, teda keď existuje také
štvorec, teda keď existuje také 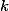 , že
, že  .
.
Takéto mechanické veci mi idú :) Keď treba použiť mozog, tak nastáva problém...
Takéto mechanické veci mi idú :) Keď treba použiť mozog, tak nastáva problém...
katka s | 31. 3. 2012 22:07:32
Fiha, ako si prisiel na tie vhodne tvary pre n? To by mi len tak nenapadlo.
Teraz nam staci toto:
+ skrytý text
Inak, tie cisla tvaru n^2+n su dvojnasobky tzv. trojuholnikovych cisel, a tie maju nejake pekne vlastnosti (staci si vygooglit triangular numbers). Ja viem, ze to az tak velmi nesuvisi s riesenim tejto ulohy, ale je to celkom zaujimave, a mozno sa to este zide pri rieseni nejakych prikladov.
Teraz nam staci toto:
+ skrytý text
Pre viac clenov si to vyrobime induktivne. Ak mame dva cleny postupnosti, ktorych sucet je tiez clen tej postupnosti, tak vieme najst vhodny clen postupnosti tak, ze ked ho pripocitame k tym dvom, tak znovu dostaneme clen tej postupnosti. Ked mame tri cleny, vieme najst nejaky stvrty, atd. Keby som napisala ako ho najst, tak to uz prezradim cele riesenie :).
Inak, tie cisla tvaru n^2+n su dvojnasobky tzv. trojuholnikovych cisel, a tie maju nejake pekne vlastnosti (staci si vygooglit triangular numbers). Ja viem, ze to az tak velmi nesuvisi s riesenim tejto ulohy, ale je to celkom zaujimave, a mozno sa to este zide pri rieseni nejakych prikladov.
BakyX | 30. 3. 2012 15:00:13
Ďakujem za hint.
+ skrytý text
+ skrytý text
V podstate keď je  v tvare
v tvare  alebo 2k^2+3k, tak aj
alebo 2k^2+3k, tak aj  je členom tejto postupnosti. To dáva odpoveď pre dve členy. Ako to dáva odpoveď pre viac členov ? Ďakujem.
je členom tejto postupnosti. To dáva odpoveď pre dve členy. Ako to dáva odpoveď pre viac členov ? Ďakujem.
katka s | 30. 3. 2012 10:20:46
Akosi som nezvladla spravne pouzit tex... Tak skusim este raz, radsej bez texu.
Hint: + skrytý text
Hint: + skrytý text
Mnozina M obsahuje vsetky cisla tvaru  \{x_n\}_{n=1}^\infty$? Moze to byt nejaky iny clen tej postupnosti?
\{x_n\}_{n=1}^\infty$? Moze to byt nejaky iny clen tej postupnosti?
katka s | 30. 3. 2012 10:18:42
Hint: + skrytý text
Mnozina M obsahuje vsetky cisla tvaru  x_n=n^2+n' border="0" src="https://prase.cz/chat/texmaker.php?tex=%24x_n%3Dn%5E2%2Bn&hash=ed6fbec7828bb73e7213" />. Aky je rozdiel dvoch po sebe iducich clenov postupnosti
x_n=n^2+n' border="0" src="https://prase.cz/chat/texmaker.php?tex=%24x_n%3Dn%5E2%2Bn&hash=ed6fbec7828bb73e7213" />. Aky je rozdiel dvoch po sebe iducich clenov postupnosti  ' alt='
' alt='  ' border="0" src="https://prase.cz/chat/texmaker.php?tex=+%24%5C%7Bx_n%5C%7D_%7Bn%3D1%7D%5E%5Cinfty%24&hash=a1fe0cdfbc82a33b55a8" />? Moze to byt nejaky iny clen tej postupnosti?
' border="0" src="https://prase.cz/chat/texmaker.php?tex=+%24%5C%7Bx_n%5C%7D_%7Bn%3D1%7D%5E%5Cinfty%24&hash=a1fe0cdfbc82a33b55a8" />? Moze to byt nejaky iny clen tej postupnosti?
BakyX | 30. 3. 2012 01:00:03
Dobrý deň. Mohol by mi prosím niekto poradiť, ako mám vyriešiť 1. úlohu odtiaľto ? http://skmo.sk/dokument.php?id=331
Tú úlohu vtedy vyriešil skoro každý, avšak ja som špeciálny prípad..Stačilo by mi povedať, odkiaľ je, ak ju niekto pozná.
Ďakujem.
Tú úlohu vtedy vyriešil skoro každý, avšak ja som špeciálny prípad..Stačilo by mi povedať, odkiaľ je, ak ju niekto pozná.
Ďakujem.
Majkl | org | 27. 3. 2012 00:12:56
Mělo by to být v pohodě sry za zdžení, Majkl
Mark | 24. 3. 2012 08:39:56
Ahoj orgové, v submitovátku mám, že jsem odevzdal úlohu č.7, ale ve výsledkovce ji mám odškrtlou, doopravili byste mi ji? Díky, M.
Štěpán | 15. 3. 2012 22:44:17
Dobrý :). A nezkusil byste to ještě někdo bez osmičky? Tedy vyřešit osmičku pomocí bodu X?
David | 15. 3. 2012 17:32:36
Štěpán: Tak už to mám.
+ skrytý text
+ skrytý text
Je to v podstatě stejný postup, jaký jsem použil na osmičku samotnou. Vezmu si tečnu z bodu X ke kružnici vepsané CED a její průsečík G s CD a "přehazováním" tečen dokážu, že NBCG je tečnový podle součtů protějších stran, přičemž použiju tvrzení osmičky.
Štěpán | 14. 3. 2012 23:03:05
Tak fajn, už jsem to pochopil. Já jsem se totiž zasekl při dokazování něčeho úplně jiného. Takže tady je něco pro Ty, kterým přijde osmička zajímavá:
Označme X průsečík AB a společné tečny kružnic vepsaných trojúhelníkům AED a BEC (tedy střed kladné stejnolehlosti, který na sebe ty dvě kružnice zobrazuje). Dokažte, že bodem X prochází i společná tečna kružnice vepsané trojúhelníku CED a čtyřúhelníku ABCD. Můžete zkusit využít řešení osmičky, respektive dokázat osmičku pomocí tohoto tvrzení (to mi přijde jako správná výzva). Mě se to dokázat nepovedlo, ale prý to platí (tvrdí geogebra). Tady je geogebří soubor: http://uloz.to/xuc3jp3/8-ggb
Označme X průsečík AB a společné tečny kružnic vepsaných trojúhelníkům AED a BEC (tedy střed kladné stejnolehlosti, který na sebe ty dvě kružnice zobrazuje). Dokažte, že bodem X prochází i společná tečna kružnice vepsané trojúhelníku CED a čtyřúhelníku ABCD. Můžete zkusit využít řešení osmičky, respektive dokázat osmičku pomocí tohoto tvrzení (to mi přijde jako správná výzva). Mě se to dokázat nepovedlo, ale prý to platí (tvrdí geogebra). Tady je geogebří soubor: http://uloz.to/xuc3jp3/8-ggb
Miroslav Olšák | org | 14. 3. 2012 21:20:31
Tam uz neni moc dalsich myslenek, to proste vyjde. Napada me leda, pamatoval jsi na toto?
+ skrytý text
+ skrytý text
Spolecne vnejsi tecny dvou kruznic jsou stejne dlouhe.
Štěpán | 14. 3. 2012 21:10:24
No fakt dobrý. To jsem přesně věděl, jenže se mi to nepovedlo dokázat. Pak už bych měl vyhráno... Mě by spíš zajímalo, jak právě to, co říkáš, dokázat.
Josef Tkadlec | 14. 3. 2012 10:13:31
Slabý hint:
+ skrytý text
Silný hint:
+ skrytý text
+ skrytý text
Equal Tangents (=tečny ke kružnici vedené z jednoho bodu se jí dotýkají stejně daleko od onoho bodu)
Silný hint:
+ skrytý text
Nakresli společnou tečnu vhodných dvou kružnic a ukaž, že nějaký čtyřúhelník je tečnový.





