Chat Prasátek

Matematická sekce

Miroslav Olšák | org | 20. 4. 2012 16:12:26

Ahoj, tu úlohu opravuji já. Zatím jsem úlohy nečetl pořádně, takže je možné, že jsem někomu body sebral neprávem (až se na úlohy pořádně podívám, tak to samozřejmě napravím).

Základní problém téhle úlohy byl, že řešitelé si zobrazili obrázek kolineací a mlčky předpokládali, že stále vypadá "tak jako před tím". Ovšem, že průsečíky se zachovají, ale vůbec už nemusí platit, že osový obraz bodu podle AB jím stále zůstane. Mám pocit, že i ty něco takového předpokládáš, když píšeš a=|BL'|=|BL|.

Rado | 19. 4. 2012 16:37:35

Podle výsledovky má ze sedmé úlohy seriálu 8 lidí jeden bod a 7 lidí 5 bodů. Můžu se zeptat, odkud pramení tak brutální úmrtnost? (Ptám se samozřejmě proto, že jsem pohořel taky a neumím si najít chybu (-: )

Olin | org | 12. 4. 2012 11:40:10

Kuba: Možná hledáš
http://people.math.sfu.ca/~cbm/aands/page_881...
(vlevo dole a pokračující vpravo nahoře)

Miško | org | 12. 4. 2012 11:10:16

Kuba: Neviem uplne presne ako to funguje, ale http://en.wikipedia.org/wiki/Discrete_Fourier... vyzera ako dobry vychodzi bod.

Miško | org | 12. 4. 2012 11:06:35

Rado: Povodne ta uloha bola navrhovana ako 4, ale po tom, co ju polovica orgov nevedela vyriesit, sme ju zadali ako 7 :)

Rado | 11. 4. 2012 17:29:09

Pítr: no, moje myšlenky se ubíraly (mimo jiné) hlavně zhruba tímto směrem, ale zkusím to udělat přesně tak, jak to píšeš ty, a když vím že to jde tak třeba na něco přijdu... Díky :)

πtr | org | 11. 4. 2012 01:09:59

Rado: Samotný trik ti ešte neprezradím, o ňom sa prípadne môžeme pobaviť aj na souse (alebo ho dám aj sem, ak bude záujem), predbežne ale aspoň hint :)

+ skrytý text

Pre sudé $n$ je riešenie pomerne jednoduché, na to si možno prišiel aj sám. A ak nie, určite ho ľahko vymyslíš ;)

Pre liché $n$ je potrebné sa pozrieť, ktoré prvočísla sa už v rozklade $n$ nachádzajú, na základe toho zvoliť vhodné prvočíslo $p$ a vytvoriť čísla $p \cdot n$ a $(p+1) \cdot n$

Rado | 11. 4. 2012 00:00:54

Tak jo, jak se sakra dělá ta pitomá (hodně umírněné slovo) sedmička???

Kuba | 10. 4. 2012 22:29:32

Pomóc! Potřeboval bych poradit s jedním problémem, a to poměrně rychle.

Mám tabulku několika funkčních hodnot, které by měly představovat určitou periodickou funkci. A já bych potřeboval tu funkcí získat rozepsanou pomocí Fourierových řad...

Téměř jistě jsem schopen si sehnat přístup k Maplu a Mathematice. Po jiném softwaru bych se musel případně poohlédnout...

Abych vás povzbudil, vyhlašuji to jako soutěž. Kdo mi jako první dokáže dát nějaký tip, který povede k vyřešení problému, ten u mě má na sousu čokoládu. (Pokud půjde o osobu, která na sous nejezdí, může si ji u mě buď převzít osobně v Jihlavě, nebo ji pošlu poštou - klidně i doporučeně.)

Pavel Šalom | 10. 4. 2012 11:27:08

Cau,
text o nerovnostech je na http://atrey.karlin.mff.cuni.cz/~paves/serial... Je to pripraveno pro knizni vydani, takze tam jsou na zacatku loga a podobne.

Kenny | 9. 4. 2012 23:44:48

Ahoj,

má první a funkční myšlenka je tato:
+ skrytý text

Menelaova věta pro $\triangle PQH$ . Rovnost poměrů lze z pravoúhlých trojúhelníků převést jen na úhly. Hodí se, že $PQDH$ je tětivový.

Ale třeba se zase najde nějaký Mirek, který bude mít chuť si s tím trochu déle hrát a nějak to "roztočí" :). Je to na známých bodech, takže to nejspíš bude i nějak vidět...

BakyX | 9. 4. 2012 18:19:37

Ešte by som sa chcel spýtať. Niekto tu niekedy dával na stiahnutie text k seriálu nerovnosti doplnený a seriálove úlohy a ich riešenia. Ja ho v PC akosi nemôžem už nájsť. Nemohli by ste to prosím hodiť sem znova ? Ďakujem.

BakyX | 9. 4. 2012 17:00:21

Dobrý deň. Mohol by mi prosím niekto poradiť s ďalším príkladom (dúfam, že nevadí, že sa toľko pýtam...)

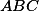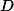Nech $\textstyle ABC$ je ostrouhlý trojuholník. Označme $\textstyle A$ päty výšok z vrcholov $\textstyle A,B$ . Nech $\textstyle D$ je ľubovoľný bod na kratšom oblúku 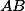$\textstyle AB$ kružnice opísanej trojuholníku 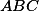$\textstyle ABC$ . Nech $\textstyle Q = BB$ a $\textstyle P = AA$ . Dokážte, že stred úsečky $\textstyle PQ$ leží na primke $\textstyle A$ .

Postačí hint. Ďakujem.

Tonda: Ďakujem za super riešenie. Je poučné.

πtr | org | 7. 4. 2012 16:18:39

Tondo: Termín je v utorok, pretože v pondelok je štátny sviatok - Velikonoce

Tonda | 7. 4. 2012 13:24:12

+ skrytý text

BÚNO $p\leq q$ a že obě jsou lichá prvočísla (to vyřešíme pak)
Tvrzení (jednoduché): všechny prvočíselné dělitele čísla $p^2+1$ jsou buď 2 nebo prvočísla tvaru $4k+1$ .
Nyní uvažujme lichá prvočísla $r$ , která dělí $p^2+1$ a jsou menší než $p$ . Taková prvočísla také dělí $2003^q+1$ a jsou menší než $q$ .
$r|2003^q+1 \Rightarrow r|2003^{2q}-1$
$r|2003^{r-1}-1$
$\Rightarrow r|2003^{NSD(r-1;2q)}-1 \Rightarrow r|2003^2-1$
$r$ má tvar $4k+1$ , a proto $r$ může být jedině $101$ , ale snadno zjistíme, že $101$ nedělí $2003^q+1$ , tzn. taková prvočísla $r$ neexistují, tzn. $p^2+1$ je složené jen ze $2$ (jen jednou, rozmyslete si) a prvočísel větších než $p$ (také jen jednou, rozmyslete si).
$p^2+1$ má tedy tvar $2t$ , kde $t$ je prvočíslo.
$2t|2003^q+1 \Rightarrow 2t|2003^{2q}-1$ , a proto $ord_{2t}(2003)|2q$ . Snadno vyloučíme hodnoty $1,2,q$ , tzn. $ord_{2t}(2003)=2q$
$2t|2003^{t-1}-1 \Rightarrow ord_{2t}(2003)|t-1 \Rightarrow 2q|t-1$
$p^2+1=2t$ a $2t$ dává zbytek $2$ po dělení $q$ , a proto $p^2$ dává zbytek $1$ po dělení $q$ , a proto $p$ dává zbytek $1$ nebo $-1$ po dělení $q$ , nyní by to mělo být lehké.
Případ když jedno prvočíslo je $2$ , pak jediné řešení bude $(2,2)$

Pozn.: Proč termín na 3.sérii je v úterý?

BakyX | 6. 4. 2012 23:13:24

Dobrý deň. Mohol by mi prosím niekto poradiť, ako vyriešiť úlohu číslo 39 z http://mks.mff.cuni.cz/common/show.php?title=... ?

Nemám najmenšie tušenie, čo s tým. Neviem to vyriešiť ani pre $\textstyle p=q$ .

Ďakujem.

BakyX | 5. 4. 2012 16:22:13

Ďakujem za super pomoc :)

+ skrytý text

Toto je dosť drsný trik. Snáď sa také raz naučím..

Josef Tkadlec | 5. 4. 2012 15:53:13

+ skrytý text

1) Stačí dokázat $\textstyle \angle PMQ+\angle PLQ=180^\circ$ .
2) Čáry $\textstyle PM$ , $\textstyle PL$ jsou isogonální v úhlu $\textstyle APB$ a podobně s $\textstyle Q$ (viz druhý díl seriálu ;)).

BakyX | 5. 4. 2012 15:15:52

Dobrý deň. Mohol by mi niekto prosím poradiť, ako vyriešiť úlohu číslo 4 z http://skmo.sk/dokument.php?id=402 ? Stačí hint. Ďakujem.

BakyX | 31. 3. 2012 22:53:15

Ďakujem za pomoc.

+ skrytý text

Tie tvary: Číslo $\textstyle n$ má požadovanú vlasnosť práve vtedy, keď je $\textstyle 8n+1$ štvorec, teda keď existuje také $\textstyle k$ , že $\textstyle 8n+1=(4k \pm 1)^2$ .

Takéto mechanické veci mi idú :) Keď treba použiť mozog, tak nastáva problém...

<< < 1 2 ... 19 20 21 ... 36 37 > >>

Kontakt

email	info (zavináč) prase.cz
pošta	Matematický korespondenční seminář KAM MFF UK Malostranské náměstí 25 118 00 Praha 1

Organizátoři

Matematický korespondenční seminář je organizovaný studenty Matematicko-fyzikální fakulty UK pod záštitou Informatického ústavu UK a Oddělení propagace a mediální komunikace MFF UK.

Partneři

Realizace projektu byla podpořena Ministerstvem školství, mládeže a tělovýchovy

Matematický korespondenční seminář

Kalendář

Z naší fotogalerie

Kontakt

Organizátoři

Partneři