Miroslav Olšák | org | 23. 10. 2012 00:20:09
Jestli resitel, ktery vyhral lonskou podzimni cast, nechape vzorak, tak asi neco delame spatne. Podporujeme dotazy. Kdyz neco neni jasne vam, je velmi pravdepodobne, ze to nebude jasne dalsim.
Treti odstavec jen upresnuje, jak provest to, co chceme v druhem odstavci, takze ho muzes preskocit (jestli chapes druhy).
Pokracovani je o tom, ze pak Pepa nezna spoustu vztahu mezi sousednimi cisly. Pritom, pokud mu na konci bude chybet byt jediny tento vztah, nebude znat presne poradi. Tato skutecnost ho donuti mit velmi specifickou strategii v nasledujicich dvou tazich. A tu mu nakonec taky vyvratime.
Treti odstavec jen upresnuje, jak provest to, co chceme v druhem odstavci, takze ho muzes preskocit (jestli chapes druhy).
Pokracovani je o tom, ze pak Pepa nezna spoustu vztahu mezi sousednimi cisly. Pritom, pokud mu na konci bude chybet byt jediny tento vztah, nebude znat presne poradi. Tato skutecnost ho donuti mit velmi specifickou strategii v nasledujicich dvou tazich. A tu mu nakonec taky vyvratime.
Rado | 22. 10. 2012 23:42:07
OK, jsem v matematickém chatu a pokračuji v "rozboru" osmičky. Abych to shrnul, v tom důkazu minimality jsem ještě tak nějak chápal druhý odstavec a mám něco jako tušení o čem je odstavec třetí a dál jsem úplně mimo. Ale už se mi nechce myslet a vůbec - je to kombinatorika, takže když mi to někdo vysvětlí, mám daleko větší šanci to pochopit ;)
Miroslav Olšák | org | 10. 10. 2012 15:57:48
Proč bylo tak těžké v osmé úloze dokázat, že menší počet pokusů nestačí? Zkuste si například rozmyslet následující (lehčí) pokračování:
Pepa sice úspěšně zjistil přesné pořadí všech 500 čísel v mém sešitě. Jenže já jsem si mezi ně někam připsal dalších 50 čísel, tedy čísla 501 až 550. Pepovy otázky jsou stále na 250 čísel. Kolik dalších otázek potřebuje Pepa k tomu, aby opět znal kompletní pořadí v mém sešitě? Stačí dvě nebo jsou potřeba tři?
Odpověď:
+ skrytý text
Pepa sice úspěšně zjistil přesné pořadí všech 500 čísel v mém sešitě. Jenže já jsem si mezi ně někam připsal dalších 50 čísel, tedy čísla 501 až 550. Pepovy otázky jsou stále na 250 čísel. Kolik dalších otázek potřebuje Pepa k tomu, aby opět znal kompletní pořadí v mém sešitě? Stačí dvě nebo jsou potřeba tři?
Odpověď:
+ skrytý text
Stačí dvě.
Rado | 9. 10. 2012 19:14:49
myslím, že existuje jednoduší : + skrytý text
Dokaž, že  (to je myslím lehké, třeba + skrytý text
(to je myslím lehké, třeba + skrytý text
to vem modulo  a ono to vyjde ;)
a ono to vyjde ;)
) a pak už stačí jen ověřit pár případůPepa S. | 9. 10. 2012 17:15:33
Ahoj, myslím, že tohle je možné řešení:+ skrytý text
Plyne to z Carmichaelovy věty (asi zbytečně silné, ale na žádné normální řešení jsem nepřišel).
http://en.wikipedia.org/wiki/Carmichael%27s_t...
http://en.wikipedia.org/wiki/Carmichael%27s_t...
Mark Daniel | 9. 10. 2012 11:31:24
Dobrý deň, je pravda, že vo Fibonacciho postupnosti sú jediné mocniny čísla 2 čísla 1,2 a 8? A ak áno, ako by sa to dalo dokázať?
Ďakujem
Ďakujem
Zbyněk | 19. 9. 2012 21:47:56
Ty tři Eulerovky se protnou v bodě + skrytý text
X(125) trojúhelníka ABC.
http://faculty.evansville.edu/ck6/encyclopedi...
http://faculty.evansville.edu/ck6/encyclopedi...
Kenny | 5. 9. 2012 19:07:18
Ahoj,
je to docela lehký
+ skrytý text a
a 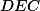 jsou podobné. Jejich Eulerovy přímky svírají úhel podobnosti. A ten ukazuje, že jejich průsečík leží na kružnici devíti bodů. Detaily si jistě domyslíte :)
jsou podobné. Jejich Eulerovy přímky svírají úhel podobnosti. A ten ukazuje, že jejich průsečík leží na kružnici devíti bodů. Detaily si jistě domyslíte :)
je to docela lehký
+ skrytý text
Dominik Teiml | 1. 9. 2012 11:57:56
Ahoj, nevím si rady s jednou úlohou, snad mi tady někdo pomůže. Označíme si paty výšek D,E,F. Je nutno dokázat, že Eulerovky trojúhelníků AFE, FBD a DEC se protínají v jednom bodě na Fuerbachovce. (Úloha pochází z College Geometry, str. 120.) Tady je můj náčrtek https://dl.dropbox.com/u/79183060/exercise73s... Chceme, aby X leželo na Fuerbachovce, symetrií potom odvodíme požadované tvrzení.
Zjistil jsem třeba, že stačí znát úhel mezi Eulerovkou a stranou. Ekvivalentně, mezi dvěma z množiny {ortocentrum, střed Fuerbachovky, těžiště, circumcenter} a nějakým vrcholem/ bodem. To proto, že pak budeme znát a
a  (protože
(protože  ), takže i
), takže i  . Takže pokud někdo jeden z těchto úhlů zná, pls dejte vědět.
. Takže pokud někdo jeden z těchto úhlů zná, pls dejte vědět.
Zjistil jsem třeba, že stačí znát úhel mezi Eulerovkou a stranou. Ekvivalentně, mezi dvěma z množiny {ortocentrum, střed Fuerbachovky, těžiště, circumcenter} a nějakým vrcholem/ bodem. To proto, že pak budeme znát
Miroslav Olšák | org | 17. 8. 2012 00:11:35
Díky, já už si říkal, že se tu budu muset pochválit sám :) Holt IMC nemá tu prestiž. A informatiky by mohlo zaujmout, kolik bodů soutěžící z MatFyzu získali, tolik mocnin dvojky se jen tak nevidí :)
Miško | org | 16. 8. 2012 23:24:40
Velke gratulacie Mirkovi, ktory skoncil 11. na IMC, co je nieco ako vysokoskolske IMO! :)
http://www.imc-math.org.uk/imc2012/IMC2012Fin...
http://www.imc-math.org.uk/imc2012/IMC2012Fin...
anonym | 27. 7. 2012 11:13:08
ahoj nahodou sem se dostal na http://atrey.karlin.mff.cuni.cz/~papa/2012/rs... zkousel sem resit ulohu 4 z 7.brezna 2012 a napadlo me jestli by ta nerovnost nemohla bejt silnejsi a sice S(p)<P^(br(P)-1)+1 nebo mohli byste mi dat protipriklad???
Alena Skálová | 24. 7. 2012 00:51:51
Sinovka je také pěkná. (-:
Miroslav Olšák | org | 23. 7. 2012 14:49:05
Ahoj, včera jsem se vrátil z PraSečí akce, kde se mimo jiné řešilo IMO (první den). Štěpán s Alčou vyřešili (na 7 bodů) jedničku (Alča sinovkou, Štěpán pěkně).
Teda mohlo to být celkově lepší a motivovanější, ale aspoň já jsem řešil dny oba:
První den:
Chci použít klasickou taktiku, řešit dvojku a jedničku si nechávat jako úlohu proti trudomyslnosti. Při pohledu na dvojku jsem se však zhrozil: Nerovnost! To nemám šanci dát, když je to dvojka a já nerovnosti prostě neumím. Naštěstí trojka byla kombinatorika, tak jsem se vrhnul na tu. Po asi dvou hodinách řešení jsem sice stále postupoval kupředu, ale stále jsem neměl ani tu část jedna.
Tak jsem šel na první úlohu. Jenže ouha, tohle vůbec není úloha proti trudomyslnosti. Tváří se to poněkud upočitatelně, ale fakt nevím, co s tím.
Vracím se k trojce. Po nějaké době vyřeším část 1, tak jdu na část 2. K mému překvapení část 2 příliš nevzdoruje, sice nestíhám ji promyslet do všech detailů, ale kostru důkazu mám myslím správnou.
Úloha 3.1:
+ skrytý text
Úloha 3.2 nikdo mi nevěří, že mi to funguje, (tak si to ani nechtěli poslechnout):
+ skrytý text
Den 2:
Opakuji taktiku. Už jsem slyšel, že pětka je Pepova (Tkadlecova) geometrie (některým spoilerům se člověk neubrání). Velmi rád bych to vyřešil, ať to můžu Pepovi pochválit, ale nevím nevím. Dosud jsem na IMO žádnou geometrii nevyřešil: dvojku na svém IMO, čtyřku na svém IMO, jedničku na tomto IMO. Ale co, tak jednou to snad dám, ne?
Zadání vypadá překvapivě jednoduše. Všechny body dávají smysl, nemám tendenci se žádných bodů zbavovat, jenže, co dál? Právě touhle jednoduchostí mě úloha dostává, co s tím?
Poznatky: + skrytý text
Opět jdu na úlohu proti trudomyslnosti. Tentokrát proti trudomyslnosti dost zabírá.
+ skrytý text
Po "vyřešení" se vracím k pětce. Jelikož už fakt netuším, zkusím zoufale rozvinout svou odvážnou hypotézu.
+ skrytý text
No vida, sice mi ještě zbývá 90 minut a šestka, ale tak nějak nevěřím, že bych to mohl vyřešit. Když to ani není kombinatorika... Radši se podívám vedle na šarády.
O čtyřce jsem se později od Pepy S. dozvěděl, že jsem ji měl špatně. Ale u trojky a pětky ještě pořád věřím, že mi to funguje, leda byste mi to vyvrátili vy...
Teda mohlo to být celkově lepší a motivovanější, ale aspoň já jsem řešil dny oba:
První den:
Chci použít klasickou taktiku, řešit dvojku a jedničku si nechávat jako úlohu proti trudomyslnosti. Při pohledu na dvojku jsem se však zhrozil: Nerovnost! To nemám šanci dát, když je to dvojka a já nerovnosti prostě neumím. Naštěstí trojka byla kombinatorika, tak jsem se vrhnul na tu. Po asi dvou hodinách řešení jsem sice stále postupoval kupředu, ale stále jsem neměl ani tu část jedna.
Tak jsem šel na první úlohu. Jenže ouha, tohle vůbec není úloha proti trudomyslnosti. Tváří se to poněkud upočitatelně, ale fakt nevím, co s tím.
Vracím se k trojce. Po nějaké době vyřeším část 1, tak jdu na část 2. K mému překvapení část 2 příliš nevzdoruje, sice nestíhám ji promyslet do všech detailů, ale kostru důkazu mám myslím správnou.
Úloha 3.1:
+ skrytý text
Myšlenka 1: stačí vyřešit úlohu pro  . Tím vlastně budu umět přinutit hráče A, aby pro danou
. Tím vlastně budu umět přinutit hráče A, aby pro danou  -prvkovou množinu přiznal jeden prvek, který není
-prvkovou množinu přiznal jeden prvek, který není  -em.
-em.
Myšlenka 2: Chci (jakožto hráč B) přinutit hráče A, aby zalhal a já si tím mohl být téměř jistý. To udělám tak, že se budu stále dokola ptát na jednoprvkovou množinu . Hráč A mi nebude chtít přiznat, že
. Hráč A mi nebude chtít přiznat, že  a proto jednou odpoví ANO.
a proto jednou odpoví ANO.
Po té už stačí (co mám jednu lež) položit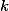 otázek na zbývající (různé od
otázek na zbývající (různé od 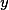 ) prvky tak, aby každá posloupnost ANO NE vedla k právě jednomu prvku. Prvek, ke kterému vede posloupnost inverzní k té, kterou podal hráč A zaručeně nemůže být roven
) prvky tak, aby každá posloupnost ANO NE vedla k právě jednomu prvku. Prvek, ke kterému vede posloupnost inverzní k té, kterou podal hráč A zaručeně nemůže být roven  .
.
Myšlenka 2: Chci (jakožto hráč B) přinutit hráče A, aby zalhal a já si tím mohl být téměř jistý. To udělám tak, že se budu stále dokola ptát na jednoprvkovou množinu
Po té už stačí (co mám jednu lež) položit
Úloha 3.2 nikdo mi nevěří, že mi to funguje, (tak si to ani nechtěli poslechnout):
+ skrytý text
Hrajme opět za situace  . Hráč A tedy nesmí dopustit, aby se B o nějakém prvku dozvěděl, že
. Hráč A tedy nesmí dopustit, aby se B o nějakém prvku dozvěděl, že  -em není. Bude si tedy u každého prvku
-em není. Bude si tedy u každého prvku  měřit hodnotu
měřit hodnotu  : kolik tahů už o něm tvrdil, že není
: kolik tahů už o něm tvrdil, že není  -em. Hráč B vždycky nabídne hráči A množinu a hráč a bude moci vynulovat
-em. Hráč B vždycky nabídne hráči A množinu a hráč a bude moci vynulovat  buď na této množině nebo na jejím doplňku. Na zbytku se
buď na této množině nebo na jejím doplňku. Na zbytku se  zvýší o jedna.
zvýší o jedna.
Chtělo by to popsat strategii, kterou množinu si hráč A bude vybírat. Ideální bude, když bude jakési jedno číslo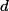 (vypočtené z hodnot
(vypočtené z hodnot  ), které bude charakterizovat "jak blbě na tom hráč A je", toto číslo se bude snažit hráč A minimalizovat.
), které bude charakterizovat "jak blbě na tom hráč A je", toto číslo se bude snažit hráč A minimalizovat.
Vysoké hodnoty dělají mnohem větší problém než nízké, ačkoli těch nízkých může být spousta (třeba
dělají mnohem větší problém než nízké, ačkoli těch nízkých může být spousta (třeba  ). Proto první pokus spočívá v:
). Proto první pokus spočívá v:

Dokáže hráč A tento součet snadno ubránit před nějakou mezí? Hráč A si samozřejmě vybere množinu s menším součtem . Tento součet je nejvýš polovina
. Tento součet je nejvýš polovina 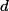 , ovšem zdvojnásobí se. Zbylá
, ovšem zdvojnásobí se. Zbylá  se sice vynulují, ale tím u nich bude
se sice vynulují, ale tím u nich bude  , tedy
, tedy 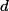 vsroste nejvýš o N. Označíme-li nové
vsroste nejvýš o N. Označíme-li nové 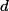 jako
jako  , máme odhad:
, máme odhad:

To ještě není žádná výhra, ovšem co takhle si zvolit mocněnec malinko menší? Tedy druhý (lepší) pokus:

Pak

S tímto umí A udržet:

Pro nějaké nezávislé na ostatních proměnných (dalo by se dopočíst jako 400, ale to jsem nestíhal).
nezávislé na ostatních proměnných (dalo by se dopočíst jako 400, ale to jsem nestíhal).
Nyní si už jen rozmyslím, zda z této meze plyne pro každé
pro každé  . Pokud by
. Pokud by  , tak by
, tak by  . Ovšem pro dostatečně velké
. Ovšem pro dostatečně velké 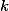 již
již

takže taková situace nemůže nastat.
Chtělo by to popsat strategii, kterou množinu si hráč A bude vybírat. Ideální bude, když bude jakési jedno číslo
Vysoké hodnoty
Dokáže hráč A tento součet snadno ubránit před nějakou mezí? Hráč A si samozřejmě vybere množinu s menším součtem
To ještě není žádná výhra, ovšem co takhle si zvolit mocněnec malinko menší? Tedy druhý (lepší) pokus:
Pak
S tímto umí A udržet:
Pro nějaké
Nyní si už jen rozmyslím, zda z této meze plyne
takže taková situace nemůže nastat.
Den 2:
Opakuji taktiku. Už jsem slyšel, že pětka je Pepova (Tkadlecova) geometrie (některým spoilerům se člověk neubrání). Velmi rád bych to vyřešil, ať to můžu Pepovi pochválit, ale nevím nevím. Dosud jsem na IMO žádnou geometrii nevyřešil: dvojku na svém IMO, čtyřku na svém IMO, jedničku na tomto IMO. Ale co, tak jednou to snad dám, ne?
Zadání vypadá překvapivě jednoduše. Všechny body dávají smysl, nemám tendenci se žádných bodů zbavovat, jenže, co dál? Právě touhle jednoduchostí mě úloha dostává, co s tím?
Poznatky: + skrytý text
Stejně dlouhé délky se dají použít k mocnosti bodu ke kružnici (tento poznatek mám již ze svého IMO). To mi dá nějaké informace o úhlech, ale zdaleka ne dostatek. Mohl by být v úloze nějaký tětivový čtyřúhelník? Nejnadějněji vypadá KMLC, ale to nefunguje. Už proto, že když je X hodně nízko, tak je úhel KML hodně placatý. Leda bych vzal nějaký bod za C-čkem, třeba kolmiště AXB. Ale to mi zní jako hodně odvážná hypotéza, s geogebrou bych to hned vyvrátil (nebo ověřil). Ale co tady, když jsem si ani nevzal rýsovací pomůcky? (stejně je moc neumím používat)
Opět jdu na úlohu proti trudomyslnosti. Tentokrát proti trudomyslnosti dost zabírá.
+ skrytý text
Jak říkává Kenny, to prostě není úloha :) Prostým dosazením (0, 0, 0) mám hodnotu v nule, dále (a, -a, 0) dává sudost funkce a následuje už jen dosazování konstant jako (1, 1, 2), (1, 2, 3), ... Sice jsem se později dozvěděl, že jsem v tom měl numerickou chybu, takže řešení bylo nakonec dvakrát delší než jsem si myslel, ale přesto v něm žádná myšlenka není. Prostě prosté dosazování konstant.
Po "vyřešení" se vracím k pětce. Jelikož už fakt netuším, zkusím zoufale rozvinout svou odvážnou hypotézu.
+ skrytý text
Ona ta úsečka KL je tak nějak nakloněná k onomu kolmišti H, takže by mohlo dokonce platit HK=HL. Tím (aby platilo, co se má dokázat) by trojúhelníky HLM, HKM měly být shodné. To by z tětivovostí HKML znamenalo, že HKM=HLM=90...
Óhóó. Do teď jsem těm úvahám dost nevěřil, ale začínají vypadat slibně. Obrázek je totiž vlastně trojúhelník AHB, kolmiště X a pak tři body C, K, L jakožto vždy průsečík výšky a Thaletovky nad stranou. Začíná to být pěkně symetrické :) Takže si předefinuji body K, L jako ty body na výškách, kde jsou pravé úhly HKB, HLA. Jestli nyní dokážu HK=HL, vyhrál jsem. Budu totiž moci zpětně ospravedlnit tuto definici bodů K, L (pootočením tvrzení k bodům A, B) a budu tak mít dost informací na to, že trojúhelníky HLM, HKM jsou vážně shodné. Na druhou stranu, když se ukáže, že to neplatí, nemám zase vůbec nic :/ Tak jdu na to ( ,
,  jsou paty příslušných výšek trojúhelníku ABH):
jsou paty příslušných výšek trojúhelníku ABH):

Vyšlo to jupííííí :)
Óhóó. Do teď jsem těm úvahám dost nevěřil, ale začínají vypadat slibně. Obrázek je totiž vlastně trojúhelník AHB, kolmiště X a pak tři body C, K, L jakožto vždy průsečík výšky a Thaletovky nad stranou. Začíná to být pěkně symetrické :) Takže si předefinuji body K, L jako ty body na výškách, kde jsou pravé úhly HKB, HLA. Jestli nyní dokážu HK=HL, vyhrál jsem. Budu totiž moci zpětně ospravedlnit tuto definici bodů K, L (pootočením tvrzení k bodům A, B) a budu tak mít dost informací na to, že trojúhelníky HLM, HKM jsou vážně shodné. Na druhou stranu, když se ukáže, že to neplatí, nemám zase vůbec nic :/ Tak jdu na to (
Vyšlo to jupííííí :)
No vida, sice mi ještě zbývá 90 minut a šestka, ale tak nějak nevěřím, že bych to mohl vyřešit. Když to ani není kombinatorika... Radši se podívám vedle na šarády.
O čtyřce jsem se později od Pepy S. dozvěděl, že jsem ji měl špatně. Ale u trojky a pětky ještě pořád věřím, že mi to funguje, leda byste mi to vyvrátili vy...
Robert | 13. 7. 2012 20:50:13
Ahoj,
Tak jsem také začal řešit úlohy z (zatím) prvního dne. Dvojka má řešení opravdu krátké (mně osobně přišla lehká), jednička mi trvala dýl, ale upižlal jsem jí.
Trojka mi přijde fakt brutální...
Zítra se pokusím vyřešit úlohy z druhého dne..
BTW- Gratuluji Pepovi, že se jeho úloha dostala na IMO! :-)
Tak jsem také začal řešit úlohy z (zatím) prvního dne. Dvojka má řešení opravdu krátké (mně osobně přišla lehká), jednička mi trvala dýl, ale upižlal jsem jí.
Trojka mi přijde fakt brutální...
Zítra se pokusím vyřešit úlohy z druhého dne..
BTW- Gratuluji Pepovi, že se jeho úloha dostala na IMO! :-)
Josef Tkadlec | 12. 7. 2012 06:00:24
Zadání už jsou i na skmo.sk.
A jinak naši: chlubte se, co jste vyřešili! Mirek to tu nečte, tak to možná ani nemusíte schovávat :).
A jinak naši: chlubte se, co jste vyřešili! Mirek to tu nečte, tak to možná ani nemusíte schovávat :).
katka | 11. 7. 2012 13:47:58
na mathlinks su:
http://www.artofproblemsolving.com/Forum/reso...
http://www.artofproblemsolving.com/Forum/reso...
? | 11. 7. 2012 11:50:11
Odkud máte úlohy? Nejsou ani na math muni, ani skmo, ani imo-official...
Sem-Nikdo | 11. 7. 2012 03:39:46
Co říkáte na úlohy z prvního dne? Mně osobně jednotka přišla velmi lehká, spísatelná na polovinu A4. Dvojka mě překvapila tím, že mám k ní řešení na pár řádků ... A trojka je napohled špatná, tu raději nezkouším. Škoda, že jsem se na to IMO nedostal.
Pavel Šalom | 12. 6. 2012 04:59:02
Cau,
nekdo se mi ozval, ze by ho zajimalo reseni te funkcionalky, tak posilam:
+ skrytý text
nekdo se mi ozval, ze by ho zajimalo reseni te funkcionalky, tak posilam:
+ skrytý text
Pro spor existuji  takova, ze
takova, ze  . Potom
. Potom
 ,
,
 ,
,
coz ale neni mozne, protoze zaroven je prvni radek vetsi nez druhy.
coz ale neni mozne, protoze zaroven je prvni radek vetsi nez druhy.





