Xellos | 9. 2. 2013 19:20:25
Co tak fyzikalne riesenie "tipnem si ze to bude mocninova funkcia a dosadenim zistim koeficienty"? :D
Mirek Hanzelka | 9. 2. 2013 16:19:52
Hezký trik s tím snížením řádu pomocí převedení na soustavu rovnic, to si musím zapamatovat :)
Vychází to úplně stejně jako předtím, ale k rovnici

se dojde mnohem rychleji. Obor hodnot je pořád omezený na záporná čísla, nemusím už ale zavádět podmínku

Nicméně, když už jsem ji zmínil, nešlo by pro nějaké rozumné funkce ukázat, že

Vychází to úplně stejně jako předtím, ale k rovnici
se dojde mnohem rychleji. Obor hodnot je pořád omezený na záporná čísla, nemusím už ale zavádět podmínku
Nicméně, když už jsem ji zmínil, nešlo by pro nějaké rozumné funkce ukázat, že
Vejtek | 9. 2. 2013 14:09:31
Ad Mirek H. a Jirka G.: Zkuste převést rovnici na soustavu dvou rovnic (tím snížíme řád).
+ skrytý text

V dalším kroku vyřešíme závislost y na x, tj. najdeme y(x).
+ skrytý text a vyřešíme separováním proměnných.
a vyřešíme separováním proměnných.
Dosadíme zpátky do druhé rovnice a tu už snad dopočítáme.
(Přiznávám, že jsem si to nezkoušel, kdyžtak napište, co vyšlo [o:)
+ skrytý text
V dalším kroku vyřešíme závislost y na x, tj. najdeme y(x).
+ skrytý text
Dosadíme zpátky do druhé rovnice a tu už snad dopočítáme.
(Přiznávám, že jsem si to nezkoušel, kdyžtak napište, co vyšlo [o:)
Mirek Hanzelka | 9. 2. 2013 11:25:38
Řešením by mohlo být například ![y(x) = -\sqrt[3]{\dfrac{9}{2}x^2} y(x) = -\sqrt[3]{\dfrac{9}{2}x^2}](https://prase.cz/chat/texmaker.php?tex=y%28x%29+%3D+-%5Csqrt%5B3%5D%7B%5Cdfrac%7B9%7D%7B2%7Dx%5E2%7D&hash=4ddb3da6defffc46c7a5) , ale záleží to na počátečních podmínkách, které jsi neudal.
, ale záleží to na počátečních podmínkách, které jsi neudal.
K tomu řešení jsem dospěl následujícím způsobem:
+ skrytý text
kde , a tedy ani žádné vyšší derivace. Zjevně platí
, a tedy ani žádné vyšší derivace. Zjevně platí

po dosazení do zadání

Pokud bychom chtěli tuto rovnici řešit integrací od a do x, tedy

dostaneme po vyřešení integrálu

rovnici

Kdyby existovala podmínka ve tvaru

např. , vyjde nám diferenciální rovnice
, vyjde nám diferenciální rovnice

kterou už vyřešíme separací proměnných. Pouze si všimneme, že pravá strana vyžaduje , pokud nehledáme v oboru komplexních čísel. Řešíme rovnici:
, pokud nehledáme v oboru komplexních čísel. Řešíme rovnici:


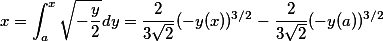
![y(x) = - \sqrt[3]{\dfrac{9}{2}\left(x + \frac{2}{3\sqrt{2}}(-y(a))^{3/2}\right)^2}. y(x) = - \sqrt[3]{\dfrac{9}{2}\left(x + \frac{2}{3\sqrt{2}}(-y(a))^{3/2}\right)^2}.](https://prase.cz/chat/texmaker.php?tex=y%28x%29+%3D+-+%5Csqrt%5B3%5D%7B%5Cdfrac%7B9%7D%7B2%7D%5Cleft%28x+%2B+%5Cfrac%7B2%7D%7B3%5Csqrt%7B2%7D%7D%28-y%28a%29%29%5E%7B3%2F2%7D%5Cright%29%5E2%7D.&hash=0593008251a239aaa7f6)
Zkouška, pro zjednodušení píšeme :
:
![y^2 = \sqrt[3]{\left(\frac{9}{2}\right)^2}(x + c)^{4/3} y^2 = \sqrt[3]{\left(\frac{9}{2}\right)^2}(x + c)^{4/3}](https://prase.cz/chat/texmaker.php?tex=y%5E2+%3D+%5Csqrt%5B3%5D%7B%5Cleft%28%5Cfrac%7B9%7D%7B2%7D%5Cright%29%5E2%7D%28x+%2B+c%29%5E%7B4%2F3%7D&hash=6216ac1693b6640f9566)
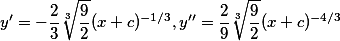

Není to asi úplně korektní postup, obzvlášť ta část s omezením oboru hodnot se mi moc nelíbí, ale nic lepšího mě nenapadá. Snad ti časem odpoví někdo povolanější.
K tomu řešení jsem dospěl následujícím způsobem:
+ skrytý text
kde
po dosazení do zadání
Pokud bychom chtěli tuto rovnici řešit integrací od a do x, tedy
dostaneme po vyřešení integrálu
rovnici
Kdyby existovala podmínka ve tvaru
např.
kterou už vyřešíme separací proměnných. Pouze si všimneme, že pravá strana vyžaduje
Zkouška, pro zjednodušení píšeme
Není to asi úplně korektní postup, obzvlášť ta část s omezením oboru hodnot se mi moc nelíbí, ale nic lepšího mě nenapadá. Snad ti časem odpoví někdo povolanější.
Jirka Guth | 8. 2. 2013 22:51:45
Ahoj, prosím vás, mám jednoduchý dotaz: Má diferenciální rovnice y^2 = 1/(y'') řešení? Děkuji.
Miroslav Olšák | org | 29. 1. 2013 01:06:19
Už máme vzoráky páté série iKSka. Vážně byly N5 a C5 tak těžké?
http://www.kms.sk/iks/files/vzorak05.pdf
http://www.kms.sk/iks/files/vzorak05.pdf
Miško | org | 17. 1. 2013 15:25:17
Caute, nahodou som narazil na tento link s nie az tak znamymi lahko formulovatelnymi otvorenymi problemami: http://mathoverflow.net/questions/100265/not-...
Štěpán | 8. 1. 2013 07:08:37
K pětce: A věděli jste, že podmínka, že K,L,M jsou středy stran je také zbytečně silná? (stačí podmínka, že K,L,M, leží na BC,CA,AB a KL||BA,KM||CA). Rozmyslete si ;-) (věřím že spoustu z vás řeší úlohu bez využití této silné podmínky)
Miroslav Olšák | org | 8. 1. 2013 00:27:22
K pětce: Víte, že podmínka tečny k opsané kružnici je zbytečná?
+ skrytý text
K sedmičce: Věru snadné, že?
+ skrytý text
+ skrytý text
Je to jediný neafinní pojem v úloze. Čili pokud obrázek zkosíme či roztáhneme, vše ostatní bude stále platit, jen ta tečna už nebude tečnou.
K sedmičce: Věru snadné, že?
+ skrytý text
Miroslav Olšák | org | 17. 12. 2012 20:25:51
Takové ordinály... Že bych napsal seriál na TeMno? :-)
Narozdíl od Vejtka budu shovívavější ke zvídavému řešiteli: Vskutku už není. Pokud uvážíme tabulku, která má ještě jeden další řádek na pozici (pozice "nekonečno"), tak obarvení ze vzoráku fungovat nebude. Tím ale nechci říct, že by vzorové řešení bylo špatně (viz Vejtkova odpověď).
(pozice "nekonečno"), tak obarvení ze vzoráku fungovat nebude. Tím ale nechci říct, že by vzorové řešení bylo špatně (viz Vejtkova odpověď).
Jinak, má ta úloha částečně nekonstruktivní řešení, které má tu výhodu, že funguje i na všelijaké obměny:
+ skrytý text
Narozdíl od Vejtka budu shovívavější ke zvídavému řešiteli: Vskutku už není. Pokud uvážíme tabulku, která má ještě jeden další řádek na pozici
Jinak, má ta úloha částečně nekonstruktivní řešení, které má tu výhodu, že funguje i na všelijaké obměny:
+ skrytý text
Všech řádků a sloupců je dohromady spočetně (viz http://cs.wikipedia.org/wiki/Spo%C4%8Detn%C3%... ) To znamená, že si je můžeme uspořádat do posloupnosti. Začneme s neobarvenou tabulkou a v každém kroku se podíváme na jeden řádek nebo sloupec naší posloupnosti. Je-li to řádek, obarvíme všechna dosud neobarvená políčka na modro, je-li to sloupec, na žluto. V každém kroku zajistíme pro příslušný řádek/sloupec, že pro něj bude splněna podmínka. Protože do té doby uběhlo pouze konečně kroků, je pouze konečně políček v daném řádku/sloupci obarvených špatně. Na "konci" (pozici  ;-) ) tohoto procesu budou všechna políčka obarvena a všechny řádky a sloupce splňovat zadání.
;-) ) tohoto procesu budou všechna políčka obarvena a všechny řádky a sloupce splňovat zadání.
Vejtek | 17. 12. 2012 18:18:39
Obávám se, že v kontextu úlohy není tato otázka relevantní, neboť cílem je obarvovat čtverečky (nebo body) sítě  (neboli
(neboli  ), kde se takový řádek nevyskytuje (jelikož
), kde se takový řádek nevyskytuje (jelikož  ). Je možné si však tuto otázku položit pro síť, kde
). Je možné si však tuto otázku položit pro síť, kde  nahradíme
nahradíme  . Není však těžké si rozmyslet, že místo
. Není však těžké si rozmyslet, že místo  lze vzít libovolný spočetný ordinál a úloha dopadne stejně, neboť na typu uspořádání nesejde.
lze vzít libovolný spočetný ordinál a úloha dopadne stejně, neboť na typu uspořádání nesejde.
Matěj Konečný | 17. 12. 2012 16:25:09
Dotaz ke čtyřce: Je v řádku č.  při řešení podle vzoráku pořád konečně mnoho žlutých čtverečků? (Úlohu jsem vyřešil, kardinálům nerozumím - do mě)
při řešení podle vzoráku pořád konečně mnoho žlutých čtverečků? (Úlohu jsem vyřešil, kardinálům nerozumím - do mě)
Miroslav Olšák | org | 16. 12. 2012 12:35:53
Kdo osmičku pochopí dřív než Rado, má u mne plus. Dá se to do deseti minut ;-)
Rado | 16. 12. 2012 11:59:07
Jaj, tím se budu prokousávat do vánoc... :)
Miroslav Olšák | org | 16. 12. 2012 01:03:45
Nejistota ohledně čtvrté úlohy je ta tam.
Vzoráky jsou tady!
(Nekonečno) http://mks.mff.cuni.cz/common/show.php?title=...
(Teorie her) http://mks.mff.cuni.cz/common/show.php?title=...
Gratuluji pravdě, která v anketě přeci jen zvítězila, ač to bylo věru těsné.
Nicméně vzoráky nejsou jen o čtyřce. Tak například vzorák osmičky doporučují čtyři ze čtyř dotázaných čtenářů. Tak co, pochopíte to taky?
Třeba Rado? :)
Na nejasnosti se ptejte, a když se vám naše vzoráky budou líbit, nezapomeňte se k tomu přiznat. Potěší nás to :-)
Vzoráky jsou tady!
(Nekonečno) http://mks.mff.cuni.cz/common/show.php?title=...
(Teorie her) http://mks.mff.cuni.cz/common/show.php?title=...
Gratuluji pravdě, která v anketě přeci jen zvítězila, ač to bylo věru těsné.
Nicméně vzoráky nejsou jen o čtyřce. Tak například vzorák osmičky doporučují čtyři ze čtyř dotázaných čtenářů. Tak co, pochopíte to taky?
Třeba Rado? :)
Na nejasnosti se ptejte, a když se vám naše vzoráky budou líbit, nezapomeňte se k tomu přiznat. Potěší nás to :-)
Štěpán | 7. 11. 2012 14:32:06
To by mě taky zajímalo
Mark Daniel | 6. 11. 2012 16:23:50
Aké bolo stručné riešenie Úlohy 5.?
Xellos | 28. 10. 2012 18:22:39
No tak pre mna je "standardne" riesenie geometrie analyika :lulzobito
Miroslav Olšák | org | 26. 10. 2012 11:50:24
Samozřejmě bych netvrdil, že jsou příklady 2. série iKS super, kdyby
neměly i skvělá řešení. K těm zajímavějším (GCA) si můžete přečíst
nápovědy.
Geometrie:
Dala se řešit standardně
+ skrytý text
+ skrytý text
Kombinatorika:
+ skrytý text
Algebra:
Zde bych podotknul, že většina snah řešitelů použít vysokoškolské
postupy selhala. Úloha je ale řešitelná vcelku elementárně.
+ skrytý text musí být sudá nebo lichá funkce.
musí být sudá nebo lichá funkce.
Je-li lichá,
+ skrytý text
+ skrytý text
neměly i skvělá řešení. K těm zajímavějším (GCA) si můžete přečíst
nápovědy.
Geometrie:
Dala se řešit standardně
+ skrytý text
Dokažte dvojrozměrnou verzi a dvakrát ji použijte.
nebo trikem+ skrytý text
Jak vypadá kulová inverze, která zobrazuje sféru opsanou  na rovinu
na rovinu  ?
?
Kombinatorika:
+ skrytý text
Ač je to zcela obecný graf, je možné popsat Mirkovu
strategii. Rozmyslete si, za jakých okolností vyhrává Pepa (na suděm počtu políček),
Mirkova strategie bude podobná.
větší nápověda:
+ skrytý text
strategii. Rozmyslete si, za jakých okolností vyhrává Pepa (na suděm počtu políček),
Mirkova strategie bude podobná.
větší nápověda:
+ skrytý text
Maximální párování
ještě větší nápověda:+ skrytý textAlgebra:
Zde bych podotknul, že většina snah řešitelů použít vysokoškolské
postupy selhala. Úloha je ale řešitelná vcelku elementárně.
+ skrytý text
Je-li lichá,
+ skrytý text
najdete nekonečně mnoho nulových hodnot
Je-li sudá,+ skrytý text
zredukujete polynom substitucí  na tutéž úlohu s menším polynomem (po několika úpravách)
na tutéž úlohu s menším polynomem (po několika úpravách)
Rado | 24. 10. 2012 20:25:58
M : Vzhledem k tomu, že nikdo jiný na to nijak nereagoval, tipuji, že problém není ve vzoráku, ale v mé (ne)funkční gramotnosti :)
A : OK, beru tě za slovo :)
A : OK, beru tě za slovo :)




