David Hruška | org | 17. 9. 2013 00:24:49
Ahoj,
Řešení problému 2 (stručné):
+ skrytý text
Problém 3:
Pro nějaká nenulová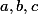 platí
platí  . Dokažte, že
. Dokažte, že  .
.
Řešení problému 2 (stručné):
+ skrytý text
Podle jedné ze základních vlastností bodu S (v českých zemích známějšího jako "Š" :-) je čtyřúhelník  , kde
, kde 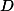 je průsečík
je průsečík 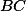 s
s  , tětivový (dá se vyúhlit). Proto
, tětivový (dá se vyúhlit). Proto  . Z mocnosti bodu
. Z mocnosti bodu 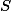 k
k  a zmíněné vlastnosti plyne
a zmíněné vlastnosti plyne  . Podle další základní vlastnosti bodu
. Podle další základní vlastnosti bodu 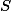 platí
platí  , tedy i
, tedy i  . Proto je
. Proto je  tečna k
tečna k  a
a  (úsekový úhel). Čili
(úsekový úhel). Čili  , což jsme měli dokázat.
, což jsme měli dokázat.
Problém 3:
Pro nějaká nenulová
BakyX | 15. 9. 2013 19:23:44
Skvelá myšlienka.
Riešenie problému 1:
+ skrytý text
Problém 2: (známa a pekná lemma)
V trojuholníku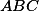 označme
označme 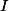 stred kružnice vpísanej,
stred kružnice vpísanej,  pätu kolmice z
pätu kolmice z 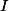 na
na 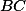 a
a 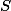 stred oblúka
stred oblúka 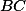 kružnice
kružnice 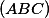 neobsahujúceho
neobsahujúceho  .
.  pretína
pretína 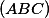 znova v
znova v 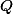 . Dokáž
. Dokáž 
Riešenie problému 1:
+ skrytý text
Pre  dostávame odhad
dostávame odhad  . Dokážeme, že všetky také
. Dokážeme, že všetky také 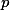 vyhovujú.
vyhovujú.
 ,
,
nakoľko .
.
nakoľko
Problém 2: (známa a pekná lemma)
V trojuholníku
Rado | 15. 9. 2013 09:39:15
Všimli jste si, jak je matematická sekce chatu neskutečně zamrzlá? Bezmála pět měsíců se tu neobjevil ani jeden příspěvek! A přestože za skoro dva a půl roku běhu nasčítala 22 stran, poslední rok zabírá jen o trošku více, než dvě strany!
Cítím se plný akce a tak to tu chci zase trošku rozproudit. Co byste říkali na maramaton (matematický maraton)? Systém je jednoduchý - vyřeším příklad a napíšu zadání nového, případně napíšu "Neznám nic neprofláklého, někdo napište zadání za mne!" (asi netřeba připomínat, ať nepíšete jako příklady zadání aktuálních soutěží) Tak schválně, jestli se toho někdo chytne :)
Příklad 1 (lehký, rozjezdový):
Najděte všechna reálná taková, že
taková, že  pro všechna kladná
pro všechna kladná 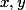
(P.S.: schovávejte řešení)
Cítím se plný akce a tak to tu chci zase trošku rozproudit. Co byste říkali na maramaton (matematický maraton)? Systém je jednoduchý - vyřeším příklad a napíšu zadání nového, případně napíšu "Neznám nic neprofláklého, někdo napište zadání za mne!" (asi netřeba připomínat, ať nepíšete jako příklady zadání aktuálních soutěží) Tak schválně, jestli se toho někdo chytne :)
Příklad 1 (lehký, rozjezdový):
Najděte všechna reálná
(P.S.: schovávejte řešení)
Martina Vaváčková | org | 17. 4. 2013 19:18:14
@Nicholas: Promiň, to je moje chyba, Tvou úlohu jsem přehlédla. Už je to ve výsledkovce opraveno.
Miroslav Olšák | org | 16. 4. 2013 22:08:22
Je to tak, reseni Kristyny Ilievove jsem opravoval dodatecne (ja jsem ten, kdo ji dal tu nulu).
Jakub Krásenský | org | 16. 4. 2013 21:56:26
Ahoj,
příslušní opravovatelé mě doplní, jestli jde opravdu o tvůj připad, Kristýnko, ale některá poštou posílaná řešení nám přišla dost pozdě. Takže rychlejší z opravovatelů si mohli myslet, že už mají všechno hotovo...
Nicholasi, tvoji úlohu taky máme a podíváme se na ni.
Zdravím.
příslušní opravovatelé mě doplní, jestli jde opravdu o tvůj připad, Kristýnko, ale některá poštou posílaná řešení nám přišla dost pozdě. Takže rychlejší z opravovatelů si mohli myslet, že už mají všechno hotovo...
Nicholasi, tvoji úlohu taky máme a podíváme se na ni.
Zdravím.
Nicholas | 16. 4. 2013 19:38:07
Mám totéž s úlohou číslo 7 (zasláno elektronicky), mám to pouze proškrtnuté. Nicméně, nijak mi to nevadí, překvapil by mě i jediný získaný bod.
Kristy | 16. 4. 2013 15:54:18
Teď koukám, že jsem to napsala pomalu jako anomym, protože jsem se nepodepsala celý jménem, tak tady je: Kristýna Ilievová
Kristý | 16. 4. 2013 14:53:35
Ahoj,
trošku mě udivuje, že jsem vám z třetí jarní série posílala příklady 1,2,4,6 a bodové hodnocení mám pouze u šestky, ačkoliv příklady 1 a 4 jsou podle proškrtnutí už uzavřené a přitom na podacím lístku mám vytištěnou váhu, která odpovídá tomu, že v obálce byli 4 listy A4, tudíž se nemohlo stát, že bych je zapoměla vložit do obálky. Prosím o vysvětlení. Děkuju
trošku mě udivuje, že jsem vám z třetí jarní série posílala příklady 1,2,4,6 a bodové hodnocení mám pouze u šestky, ačkoliv příklady 1 a 4 jsou podle proškrtnutí už uzavřené a přitom na podacím lístku mám vytištěnou váhu, která odpovídá tomu, že v obálce byli 4 listy A4, tudíž se nemohlo stát, že bych je zapoměla vložit do obálky. Prosím o vysvětlení. Děkuju
Alena Skálová | 14. 4. 2013 18:28:32
Ahoj,
já čerpám většinu svých znalostí o kuželosečkách ze skript Pavla Pecha (https://www.pf.jcu.cz/stru/katedry/m/knihy/Ku...). Prolíná se v nich analytický a syntetický přístup, analytiky je mnohem víc, ale něco k syntetice tam také najdeš (hlavně v prvních čtyřech kapitolách). Jsou to sice vysokoškolská skripta, ale právě ty syntetické části jsou myslím pochopitelné i "středoškolsky".
já čerpám většinu svých znalostí o kuželosečkách ze skript Pavla Pecha (https://www.pf.jcu.cz/stru/katedry/m/knihy/Ku...). Prolíná se v nich analytický a syntetický přístup, analytiky je mnohem víc, ale něco k syntetice tam také najdeš (hlavně v prvních čtyřech kapitolách). Jsou to sice vysokoškolská skripta, ale právě ty syntetické části jsou myslím pochopitelné i "středoškolsky".
byk7 | 13. 4. 2013 17:13:30
Zdravím,
nevíte/nemáte materiály o syntetickém zkoumání a vlastnostech kuželoseček? Tím mám na mysli hlavně paraboly, hyperboly a elipsy.
Budu rád za každý materiál.
díky.
nevíte/nemáte materiály o syntetickém zkoumání a vlastnostech kuželoseček? Tím mám na mysli hlavně paraboly, hyperboly a elipsy.
Budu rád za každý materiál.
díky.
Martin Töpfer | org | 29. 3. 2013 12:12:26
Pozor! Oprava zadání!
V zadání sedmé úlohy Myšmaše má být suma od 1 do n.
http://mks.mff.cuni.cz/common/show.php?title=...
V zadání sedmé úlohy Myšmaše má být suma od 1 do n.
http://mks.mff.cuni.cz/common/show.php?title=...
Jakub Krásenský | org | 24. 3. 2013 14:20:49
Pozor! Oprava zadání!
Změnilo se zadání šesté úlohy Myšmaše. Deltoid musí být konvexní čtyřúhelník. Tak si stáhněte aktuální zadání a ukažte čtyřúhelníkům, zač je toho loket! http://mks.mff.cuni.cz/common/show.php?title=...
Změnilo se zadání šesté úlohy Myšmaše. Deltoid musí být konvexní čtyřúhelník. Tak si stáhněte aktuální zadání a ukažte čtyřúhelníkům, zač je toho loket! http://mks.mff.cuni.cz/common/show.php?title=...
Filip Hlásek | org | 17. 2. 2013 00:18:42
Jak se výtah pohyboval v sedmé úloze nedávno odeslané série si můžete vyzkoušet zde:
https://mks.mff.cuni.cz/hlavni_strana/vytah.swf
Této vychytávce dalo vzniknout mnoho PraSečích orgů...
Míša úlohu navrhla,
Martina klikátko nakódila,
Šavlík poradil,
Mirek to potom hodil na web,
Pepa mě přemluvil,
abych sem o tom nakonec napsal...
Jak se vám to líbí?
+ skrytý text
https://mks.mff.cuni.cz/hlavni_strana/vytah.swf
Této vychytávce dalo vzniknout mnoho PraSečích orgů...
Míša úlohu navrhla,
Martina klikátko nakódila,
Šavlík poradil,
Mirek to potom hodil na web,
Pepa mě přemluvil,
abych sem o tom nakonec napsal...
Jak se vám to líbí?
+ skrytý text
Tak vidíte jak to v PraSeti funguje:
nejstarší už jenom radí,
trochu méně staří přemlouvají ostatní,
ti nejproduktivnější makají,
a zelenáči tvoří...
nejstarší už jenom radí,
trochu méně staří přemlouvají ostatní,
ti nejproduktivnější makají,
a zelenáči tvoří...
Matěj Konečný | 13. 2. 2013 14:06:15
Děkuju moc :). Je to zajímavý řešení, ale nikdy bych na to nepřišel.
Kenny | 13. 2. 2013 13:46:22
Zdravím,
je to vcelku známý výsledek už z dob Leonharda Eulera.
Více tu.
+ skrytý text
je to vcelku známý výsledek už z dob Leonharda Eulera.
Více tu.
+ skrytý text
Matěj Konečný | 12. 2. 2013 23:09:41
Narazil jsem na zajímavou úlohu:
Známe poloměry opsané i vepsané kružnice obecného trojúhelníku. Jaká je vzdálenost jejich středů?
Vůbec jsem s ní nehnul, pomůže mi někdo tady? :)
Pozn: Vůbec nevím, jestli je tímto ta vzdálenost jednoznačně definována. Pokud ne, pomohla by třeba informace, že je trojúhelník pravoúhlý? Rovnoramenný?
Známe poloměry opsané i vepsané kružnice obecného trojúhelníku. Jaká je vzdálenost jejich středů?
Vůbec jsem s ní nehnul, pomůže mi někdo tady? :)
Pozn: Vůbec nevím, jestli je tímto ta vzdálenost jednoznačně definována. Pokud ne, pomohla by třeba informace, že je trojúhelník pravoúhlý? Rovnoramenný?
Kristýna | 11. 2. 2013 18:30:44
Řešení normálně posílám poštou a teď jsem zjistila, že mi k úloze 4 zůstal na stole obrázek, který je u mého k řešení nutný. Pošta zavřela... :( Chtěla bych to tedy ještě dnes ten dodatek poslat elektronicky, bylo by možné, aby mi někdo z orgů ještě dnes umožnil elektronické odesílání, anebo můžu to někomu z orgů poslat přes e-mail?
Jirka Guth | 9. 2. 2013 20:33:03
Hezky, díky Mirku, že sis dal takovou práci.
Co se týče počátečních podmínek, tak je y = konst. a y' = konst.
Nechci moc prozrazovat, protože jsem to plánoval jako součást řešení jednoho příkladu ve Fykosu a nechci si připadat tak, jako že na Makosí chat chodím pro řešení Fykosu, ale jak tak na to koukám, asi to vymyslím jinak.
Co se týče počátečních podmínek, tak je y = konst. a y' = konst.
Nechci moc prozrazovat, protože jsem to plánoval jako součást řešení jednoho příkladu ve Fykosu a nechci si připadat tak, jako že na Makosí chat chodím pro řešení Fykosu, ale jak tak na to koukám, asi to vymyslím jinak.
Xellos | 9. 2. 2013 19:20:25
Co tak fyzikalne riesenie "tipnem si ze to bude mocninova funkcia a dosadenim zistim koeficienty"? :D





