Miško | org | 18. 10. 2013 14:02:45
byk7: Ja si myslim, ze je to vec definicie, prave preto sa pytam. Mozno lepsia otazka by bola: "Co sa povazuje za 5-uholnik v matematickej olympiade?"
byk7 | 14. 10. 2013 21:19:51
@Misko: Takove OT, ale mam za to, ze  -uhelnik, ma
-uhelnik, ma  vnitrnich uhlu. Peticipa hvezda jich ma ale 10. Nebo se pletu?
vnitrnich uhlu. Peticipa hvezda jich ma ale 10. Nebo se pletu?
Rado | 10. 10. 2013 14:56:28
Hinty jsou cool, ale (jestli je plánujete, jak jsem pochopil, zveřejňovat pravidelně) možná by nebylo od věci je nestrkat sem a místo toho pro ně vymyslet nějaké spešl místo :)
Není to úplně moje starost, ale rád bych všem připomněl, že je v běhu první série TRiKS, že na ní zbývají už jen čtyři dny a (protože já už ji mám za sebou) potvrdit, že je fakt cool :) (a taky, že je i pro orgy).
A co se týče maramatonu, jsem rád že se to takhle rozběhlo a tudíž bych rád taktéž přispěl svou troškou, takže: Problém 12:
+ skrytý text
Problém 13: Každé celé číslo obarvíme červenou nebo modrou barvičkou. Víme, že v libovolné množině za sebou jdoucích čísel je absolutní hodnota rozdílu počtu červených a modrých čísel maximálně 1000. Ukažte, že existuje 2000 za sebou jdoucích čísel, mezi kterými je právě 1000 modrých (a právě 1000 červených).
Není to úplně moje starost, ale rád bych všem připomněl, že je v běhu první série TRiKS, že na ní zbývají už jen čtyři dny a (protože já už ji mám za sebou) potvrdit, že je fakt cool :) (a taky, že je i pro orgy).
A co se týče maramatonu, jsem rád že se to takhle rozběhlo a tudíž bych rád taktéž přispěl svou troškou, takže: Problém 12:
+ skrytý text
Nechť průsečík  a
a 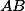 s
s  jsou body
jsou body 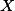 a
a 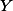 . Protože úhly
. Protože úhly  a
a  jsou shodné, jsou shodné i
jsou shodné, jsou shodné i  a
a  , takže
, takže  je rovnoramenný trojúhelník, takže osa úsečky
je rovnoramenný trojúhelník, takže osa úsečky 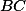 splývá s osou úhlu
splývá s osou úhlu  , neboli s osou úhlu
, neboli s osou úhlu  . Analogicky osa
. Analogicky osa  splývá s osou
splývá s osou  , takže tyto osy se protínají ve vepsišti
, takže tyto osy se protínají ve vepsišti  , tudíž tímto bodem prochází i osa
, tudíž tímto bodem prochází i osa  , neboli osa
, neboli osa  , což jsme chtěli dokázat.
, což jsme chtěli dokázat.
Q.E.D.
Q.E.D.
Problém 13: Každé celé číslo obarvíme červenou nebo modrou barvičkou. Víme, že v libovolné množině za sebou jdoucích čísel je absolutní hodnota rozdílu počtu červených a modrých čísel maximálně 1000. Ukažte, že existuje 2000 za sebou jdoucích čísel, mezi kterými je právě 1000 modrých (a právě 1000 červených).
Miško | org | 10. 10. 2013 13:58:11
@Pepa T.: Co je to patuholnik? Je to aj pravidelna 5-cipa hviezda?
E.T. | org | 7. 10. 2013 23:34:34
Milí Přátelé!
Nevyřešili jste všechny úlohy první podzimní série? Nezoufejte! Přicházíme totiž s novinkou -- uveřejňováním hintů, se kterými máte jedinečnou možnost vyřešit i ty nejtěžší úlohy z každé série, i když si na ně normálně netroufnete. Zkuste si to, třeba zjistíte, že sedmičky a osmičky nejsou tak nezvladatelné, jak se zdají, a příště je možná zvládnete i bez rad.
úloha 1:
(i)+ skrytý text
(ii)+ skrytý text
úloha 2:
+ skrytý text
úloha 3:
+ skrytý text
úloha 4:
(i) + skrytý text
(ii) + skrytý text
úloha 5:
+ skrytý text
úloha 6:
+ skrytý text
úloha 7:
+ skrytý text
úloha 8:
+ skrytý text
Za všechny organizátory vám přeji spoustu vyřešených úloh,
E.T.
pozn.: Pokud ani s hinty nezvládnete úlohu dořešit, rozhodně se nestyďte ozvat se a požádat o další rady, od toho tu jsme. Nikdy se ale nebavte o úlohách dříve než 24 hodin po termínu odeslání dané série.
Nevyřešili jste všechny úlohy první podzimní série? Nezoufejte! Přicházíme totiž s novinkou -- uveřejňováním hintů, se kterými máte jedinečnou možnost vyřešit i ty nejtěžší úlohy z každé série, i když si na ně normálně netroufnete. Zkuste si to, třeba zjistíte, že sedmičky a osmičky nejsou tak nezvladatelné, jak se zdají, a příště je možná zvládnete i bez rad.
úloha 1:
(i)+ skrytý text
Jde to.
(ii)+ skrytý text
Použijte čtverce 5*5 1-krát, 4*4 2-krát, 3*3 1-krát, 2*2 3-krát, 1*1 3-krát.
úloha 2:
+ skrytý text
Každý střih protne každou z 2*(n-1) "vnitřních" čar tabulky nejvýše jednou.
úloha 3:
+ skrytý text
Dokažte, že když jsou v některém řádku těsně vedle sebe barvy A, B a C, pak se ve sloupci s barvou B musí střídat barvy B a D.
úloha 4:
(i) + skrytý text
Zkuste si nejdříve zjistit, kolika způsoby lze vybarvit volné políčko, políčko, barvu jehož jedné strany už známe, a políčko, barvu jehož 2 stran už známe.
(ii) + skrytý text
Vybarvujte papír postupně po čtverečcích.
úloha 5:
+ skrytý text
Začněte s pravoúhlým trojúhelníkem s celočíselnými délkami stran a vhodně ho "nafoukněte".
úloha 6:
+ skrytý text
Jde to.
úloha 7:
+ skrytý text
Zkuste obarvit nějaká políčka černě tak, aby spojnice horní a dolní strany nutně šla přes nějaké z černých polí a zamyslete se, jestli umí Martina zařídit, aby všechna maxima byla mimo tato černá pole.
úloha 8:
+ skrytý text
Postupujte sporem a dokazujte postupně ukažte, že platí tyto poznatky:
(i) + skrytý text
(ii) + skrytý text
(iii) + skrytý text
(iv) + skrytý text
(i) + skrytý text
Některý řádek je celý jednobarevný.
(ii) + skrytý text
BÚNO jsou první řádek a první sloupec celé černé.
(iii) + skrytý text
Úhlopříčky zbylého čtverce jsou celé bílé.
(iv) + skrytý text
Spor s nutností skoro-bílých a současně skoro-černých řádků/sloupců.
Za všechny organizátory vám přeji spoustu vyřešených úloh,
E.T.
pozn.: Pokud ani s hinty nezvládnete úlohu dořešit, rozhodně se nestyďte ozvat se a požádat o další rady, od toho tu jsme. Nikdy se ale nebavte o úlohách dříve než 24 hodin po termínu odeslání dané série.
Josef Tkadlec | 6. 10. 2013 23:47:06
Myslím, že týden je moc, tak píšu řešení. Neumím ho úplně motivovat, ale snad funguje:
Řešení Problému 11:
+ skrytý text
Problém 12: V pětiúhelníku mají všechny vnitřní úhly stejnou velikost. Dokažte, že osa úhlu
mají všechny vnitřní úhly stejnou velikost. Dokažte, že osa úhlu  a osy úseček
a osy úseček 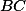 a
a  procházejí jedním bodem.
procházejí jedním bodem.
Řešení Problému 11:
+ skrytý text
Označme kořeny  . Z vietových vztahů přeformulujeme podmínku na
. Z vietových vztahů přeformulujeme podmínku na  a chceme dokázat, že
a chceme dokázat, že  .
.
Z Cauchy-Schwarze a s využitím podmínky máme
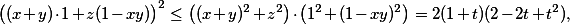
kde . Po roznásobení vyjde, že chceme
. Po roznásobení vyjde, že chceme  , tedy
, tedy  . Takovou dvojici
. Takovou dvojici 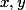 ale určitě najdeme, protože jinak by bylo
ale určitě najdeme, protože jinak by bylo  , spor.
, spor.
Z Cauchy-Schwarze a s využitím podmínky máme
kde
Problém 12: V pětiúhelníku
BakyX | 29. 9. 2013 23:46:00
Riešenie problému 10:
+ skrytý text
Problém 11: Predpokladajme, že všetky korene rovnice sú reálne čísla a navyše platí
sú reálne čísla a navyše platí  . Dokážte
. Dokážte  .
.
+ skrytý text
Označme  ostatné dotykové body na
ostatné dotykové body na  . Z rovnosti dotyčníc platia vzťahy
. Z rovnosti dotyčníc platia vzťahy  ,
,  ,
,  . Potom platia vzťahy:
. Potom platia vzťahy:



Odtiaľ ,
,  . Preto:
. Preto:
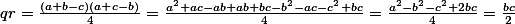
Čo je presne obsah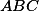 .
.
Odtiaľ
Čo je presne obsah
Problém 11: Predpokladajme, že všetky korene rovnice
Kuba | 29. 9. 2013 20:01:38
Omlouvám se, to, z čeho vznikl podivný znak "²" v řešení 9 znamená "na druhou" :)
Kuba | 29. 9. 2013 19:57:32
Řešení problému 9 + skrytý text
Problém 10: Něco trošku lehčího a užitečného: V trojúhelníku ABC s pravým úhlem u vrcholu A označme dotek kružnice vepsané se stranou BC jako X. Dokažte, že Obsah ABC = BX*CX
Očíslujme matematiky postupně 1 až n a označme P(k) počet přátel matematika s číslem k. Stačí dokázat, že průměrný počet přátelství jednoho člověka je menší rovno průměrnému množství přátelů přátel jednoho člověka. Pro zjištění množství přátelů přátel člověka jistě vezmeme přátele každého člověka právě tolikrát, kolik má přátel. Tedy dokazujeme, že:
(p(1)² +...+ P(n)²)/(P(1)+...+P(n)) >=(P(1)+...+P(n))/n
Což ekvivalentně upravíme na n*(p(1)² +...+ P(n)²) >=(P(1)+...+P(n))²
Což je přesně Cauchy-Schwarzova nerovnost, tudíž tvrzení ze zadání je pravda.
(p(1)² +...+ P(n)²)/(P(1)+...+P(n)) >=(P(1)+...+P(n))/n
Což ekvivalentně upravíme na n*(p(1)² +...+ P(n)²) >=(P(1)+...+P(n))²
Což je přesně Cauchy-Schwarzova nerovnost, tudíž tvrzení ze zadání je pravda.
Problém 10: Něco trošku lehčího a užitečného: V trojúhelníku ABC s pravým úhlem u vrcholu A označme dotek kružnice vepsané se stranou BC jako X. Dokažte, že Obsah ABC = BX*CX
BakyX | 26. 9. 2013 23:01:41
Riešenie problému 8:
+ skrytý text . Stačí ukázať deliteľnosť toho výrazu číslami
. Stačí ukázať deliteľnosť toho výrazu číslami  .
.
Zrejme a
a  , takže po umocnení každej z týchto kongruencií na
, takže po umocnení každej z týchto kongruencií na  a sčítaní máme
a sčítaní máme  .
.
Zrejme a
a  , takže podobne máme
, takže podobne máme  .
.
Problem 9:
Ak v skupine matematikov je každý s niekým spriatelený (priateľstvo je symetrické), tak medzi nimi existuje matematik taký, že priemerný počet priateľov všetkých jeho priateľov nie je menší než priemerný počet priateľov všetkých členov uvedenej skupiny. Dokážte.
+ skrytý text
Zrejme
Zrejme
Problem 9:
Ak v skupine matematikov je každý s niekým spriatelený (priateľstvo je symetrické), tak medzi nimi existuje matematik taký, že priemerný počet priateľov všetkých jeho priateľov nie je menší než priemerný počet priateľov všetkých členov uvedenej skupiny. Dokážte.
abstract nonsense | 26. 9. 2013 22:16:11
Reseni problemu 7:
+ skrytý text
Problem 8: Ukažte, že dělí
dělí  pro všechna přirozená
pro všechna přirozená  .
.
+ skrytý text
Klasicky roznasobme a pak vhodne rozlozme na soucin.




Vsimneme si, ze je prvociselny rozklad, tedy
je prvociselny rozklad, tedy  Avsak
Avsak  , tedy jedine
, tedy jedine  prichazi v uvahu, z toho dostaneme dve reseni
prichazi v uvahu, z toho dostaneme dve reseni  a to
a to  .
.
Vsimneme si, ze
Problem 8: Ukažte, že
Josef Tkadlec | 26. 9. 2013 18:32:05
Stručné řešení Problému 6:
+ skrytý text
Zdálo se mi to spíš těžké, tak pro změnu něco lehčího:
Problém 7: Vyřešte v přirozených číslech rovnici
+ skrytý text
Jakožto druhé průsečíky příslušných kružnic jsou body 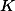 ,
, 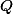 středy spirálních podobností zobrazujících
středy spirálních podobností zobrazujících 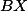 na
na  , respektive
, respektive 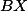 na
na  (orientovaně). Chceme body
(orientovaně). Chceme body 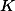 a
a 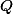 nějak spojit, tak (trik!) dokreslíme středy
nějak spojit, tak (trik!) dokreslíme středy 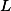 ,
, 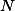 úseček
úseček 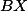 ,
,  , protože ty na sebe přejdou v obou spirálkách. Navíc už v obrázku de facto máme střed
, protože ty na sebe přejdou v obou spirálkách. Navíc už v obrázku de facto máme střed 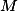 úsečky
úsečky 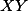 , protože chordála
, protože chordála  půlí společnou tečnu
půlí společnou tečnu 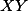 .
.
Zbývá si vyúhlit pár drobností (třeba to, že trojúhelník je podobný oběma
je podobný oběma  a
a  ), použít ostatní kružnice skrz středy spirálek (např.
), použít ostatní kružnice skrz středy spirálek (např.  skrz
skrz 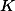 ) a pak už to jen poslepovat.
) a pak už to jen poslepovat.
Z

plyne, že body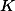 ,
, 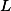 ,
,  ,
, 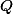 ,
, 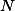 leží na jedné kružnici a z toho už dostaneme i
leží na jedné kružnici a z toho už dostaneme i

Zbývá si vyúhlit pár drobností (třeba to, že trojúhelník
Z
plyne, že body
Zdálo se mi to spíš těžké, tak pro změnu něco lehčího:
Problém 7: Vyřešte v přirozených číslech rovnici
Josef Tkadlec | 21. 9. 2013 22:00:59
Ad Problém 5:
+ skrytý text
+ skrytý text
Ve druhé možnosti má být  , takže součet vyjde
, takže součet vyjde  .
.
Když to vyjde takhle, tak to musí jít nahlédnout :).
Když to vyjde takhle, tak to musí jít nahlédnout :).
BakyX | 19. 9. 2013 21:09:12
Tonda, zadania nemusíš skrývať :) Rešpekt za tú brutálnu rovnicu.
Riešenie problému 5:
+ skrytý text
Problem 6: Kružnice sa pretínajú v
sa pretínajú v  .
. 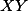 je spoločné dotyčnica týchto kružníc, ktorá je bližšie k
je spoločné dotyčnica týchto kružníc, ktorá je bližšie k  a
a 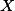 je na
je na  a
a 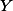 na
na  .
.  pretína
pretína  druhý-krát v
druhý-krát v 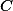 a
a  pretína
pretína  v
v  . Nech
. Nech  je prienik
je prienik 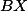 a
a  . Dokáž, že ak
. Dokáž, že ak 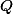 je druhý priesečník kružníc
je druhý priesečník kružníc 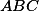 a
a  , tak
, tak  .
.
Riešenie problému 5:
+ skrytý text
Nech 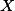 je nejaký konkrétny bod.
je nejaký konkrétny bod.
Ak je medzi vybranými, tak jeho susedné body nemôžeme vybrať. Ostáva nám vybrať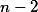 bodov z
bodov z  tak, aby sme nevybrali susedné, pričom teraz môžeme vybrať oba krajné naraz.
tak, aby sme nevybrali susedné, pričom teraz môžeme vybrať oba krajné naraz.
Tento problém je ekvivalentný určeniu počtu poradí čísel v ktorých je
v ktorých je 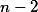 jednotiek a zvyšok sú nuly, aby dve
jednotiek a zvyšok sú nuly, aby dve 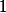 nestáli vedľa seba. To spravíme takto: Rozmiestnime nuly. Jednotky môžu stať len medzi nulami alebo na konci alebo na začiatku. Počet výberov miest pre ne je
nestáli vedľa seba. To spravíme takto: Rozmiestnime nuly. Jednotky môžu stať len medzi nulami alebo na konci alebo na začiatku. Počet výberov miest pre ne je  .
.
Analogicky keď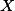 nie je medzi vybranými, tak je počet jednotiek
nie je medzi vybranými, tak je počet jednotiek  a počet núl
a počet núl 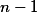 , takže
, takže  možností.
možností.
Dokopy máme možností.
možností.
Ak je medzi vybranými, tak jeho susedné body nemôžeme vybrať. Ostáva nám vybrať
Tento problém je ekvivalentný určeniu počtu poradí čísel
Analogicky keď
Dokopy máme
Problem 6: Kružnice
Tonda | 19. 9. 2013 19:37:12
Ahoj,
Problém 4
+ skrytý text
Problém 5
+ skrytý text
Problém 4
+ skrytý text
Substituce  .
.
Po úpravě dostaneme:
Pokud , pak pomocí AG
, pak pomocí AG  , což nám nedá žádné řešení, protože
, což nám nedá žádné řešení, protože  by bylo větší než
by bylo větší než  . Tímto argumentem můžeme také vyloučit případ, že
. Tímto argumentem můžeme také vyloučit případ, že  .
.
Nyní víme, že obě čísla a
a  jsou větší než
jsou větší než 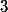 , a proto
, a proto  .
.
Substituce . Platí
. Platí



Druhá derivace nemá žádný kořen, a proto první derivace může mít maximálně jeden kořen, který je . Můžeme také ověřit že
. Můžeme také ověřit že  je lokální minimum funkce
je lokální minimum funkce  s hodnotou
s hodnotou  .
.
Řešení původní rovnice jsou tedy případy rovnosti, které se můžou nastat pouze za podmínky , z čehož plyne
, z čehož plyne  neboli
neboli  . Zkouškou snadno zjistíme, že nalezené řešení skutečně vyhovuje.
. Zkouškou snadno zjistíme, že nalezené řešení skutečně vyhovuje.
Po úpravě dostaneme:
Pokud
Nyní víme, že obě čísla
Substituce
Druhá derivace nemá žádný kořen, a proto první derivace může mít maximálně jeden kořen, který je
Řešení původní rovnice jsou tedy případy rovnosti, které se můžou nastat pouze za podmínky
Problém 5
+ skrytý text
Kolika způsoby můžeme vybrat  bodů navzájem nesousedících z 2n bodů na kružnici?
bodů navzájem nesousedících z 2n bodů na kružnici?
David Hruška | org | 18. 9. 2013 15:40:49
Xellos: Díky za doplnění, opravdu má být v Problému 3  , nějak jsem to opomněl. A jinak pěkné řešení!
, nějak jsem to opomněl. A jinak pěkné řešení!
πtr | org | 18. 9. 2013 03:43:04
Xellos: díky za upozornenie, teraz by snáď spoiler tag mal fungovať správne
Xellos | 17. 9. 2013 17:58:46
To nevadi ze na uvodnej stranke (aspon mne: Chrome, Win7) nefunguje spoiler tag?
Xellos | 17. 9. 2013 17:56:33
Enjoy the spoiler...
+ skrytý text
+ skrytý text
abstract nonsense, z tej druhej rovnosti fakt nevidim ako si dostal  ... surove roznasobenie a mlaticka alebo je tam nejaky pekny medzikrok?
... surove roznasobenie a mlaticka alebo je tam nejaky pekny medzikrok?
Kazdopadne, ponukam Problem 3.1 (working title: Ihla v kope sena). Ciel: v zadani nieco chyba; najdite co. A este bonus: Z toho vyplyva ze abstractove riesenie je neuplne; najdite v ktor(om|ych) krok(u|och) je diera.
Riesenie problemu 3.1:
+ skrytý text
Ine riesenie problemu 3 (spoiler alert: v podstate obsahuje predosly spoiler):
+ skrytý text
Kazdopadne, ponukam Problem 3.1 (working title: Ihla v kope sena). Ciel: v zadani nieco chyba; najdite co. A este bonus: Z toho vyplyva ze abstractove riesenie je neuplne; najdite v ktor(om|ych) krok(u|och) je diera.
Riesenie problemu 3.1:
+ skrytý text
Vazba plati trivialne pre  . Ak teda napr. polozime vsetky 3 cisla rovne 2, tak mame platnu vazbu a
. Ak teda napr. polozime vsetky 3 cisla rovne 2, tak mame platnu vazbu a  . V zadani teda chyba spomenut ze
. V zadani teda chyba spomenut ze  .
.
Bonus: tipujem ze v rieseni 2. rovnosti (ta este plati), asi tam je niekde delenie .
.
Bonus: tipujem ze v rieseni 2. rovnosti (ta este plati), asi tam je niekde delenie
Ine riesenie problemu 3 (spoiler alert: v podstate obsahuje predosly spoiler):
+ skrytý text
Ak su nejake 2 cisla rovnake, BUNV  , z vazby hned vidime ze vsetky 3 su rovnake. Predpokladajme teda dalej ze su vsetky 3 rozne.
, z vazby hned vidime ze vsetky 3 su rovnake. Predpokladajme teda dalej ze su vsetky 3 rozne.
Kazdu rovnost z vazby si prepiseme do tvaru (dalsie 2 mame cyklickou zamenou). Ich vynasobenie da
(dalsie 2 mame cyklickou zamenou). Ich vynasobenie da  , z coho uz vidno ze
, z coho uz vidno ze  .
.
A vidime ze ak , tak by sme delili nulou.
, tak by sme delili nulou.
Kazdu rovnost z vazby si prepiseme do tvaru
A vidime ze ak
abstract nonsense | 17. 9. 2013 16:39:19
Reseni Problemu 3:
+ skrytý text
Problem 4:
Naleznete vsechna splnujici
splnujici

+ skrytý text
Zrejme z prvni rovnosti plati

Potom v druhe rovnosti

Neboli pro
pro  . Dosazenim tohohle do prvni rovnosti dostaneme
. Dosazenim tohohle do prvni rovnosti dostaneme

Neboli , potom
, potom

Pokud , pak z prvni rovnosti
, pak z prvni rovnosti  a opet
a opet  .
.
Potom v druhe rovnosti
Neboli
Neboli
Pokud
Problem 4:
Naleznete vsechna





