Josef Svoboda | 24. 11. 2013 17:20:08
Ahoj OD.
Toto pojmenování je pro mě také trochu záhadou. Nicméně v matematice platí, že každý si může pojmenovat cokoliv jak se mu zlíbí. Pokud ovšem napíše, o co vlastně jde.
Mrkvovo-salámové lemma + skrytý text
Bismarckovo lemma + skrytý text
Toto pojmenování je pro mě také trochu záhadou. Nicméně v matematice platí, že každý si může pojmenovat cokoliv jak se mu zlíbí. Pokud ovšem napíše, o co vlastně jde.
Mrkvovo-salámové lemma + skrytý text
říká, že v trojúhelníku ABC dělí osa úhlu BAC stranu BC v poměru b:c. Někdy se mu také říká věta o ose úhlu: http://en.wikipedia.org/wiki/Angle_bisector_t...
Bismarckovo lemma + skrytý text
říká, že pokud D je průsečík osy úhlu BAC a kružnice opsané trojúhelníku ABC, pak 1) D je střed oblouku BC, na kterém neleží bod A, 2) pokud E (resp. F) je průsečík strany AB (resp. AC) a osy úhlu ADB (resp. ADC), pak je přímka EF rovnoběžná se stranou BC.
OD | 23. 11. 2013 21:43:31
Zdravím,
chtěl bych se zeptat, co se myslí mrkvo-salámovým a Bismarckovým lemmatem ze závěru vzoráku 2. série?
chtěl bych se zeptat, co se myslí mrkvo-salámovým a Bismarckovým lemmatem ze závěru vzoráku 2. série?
Miško | org | 17. 11. 2013 10:28:19
Nj, mala tam byt dokazatelnost a nie platnost...
Miroslav Olšák | org | 16. 11. 2013 11:42:19
No, trochu podvadis
+ skrytý text
+ skrytý text
Ze se veta neda dokazat, nezarucuje, ze "neplati" -- jsou tvrzeni, ktera se nedaji vyvratit ani dokazat. To souvisi s Godelovou vetou o neuplnosti a halting problemem. (ale nechce se mi to tu vysvetlovat, nikdo by to nepochopil)
Ba co hur, ze se veta da dokazat uplne nezarucuje, ze "plati". Logika je holt nejnelogictejsi oblast matematiky ;-)
Ba co hur, ze se veta da dokazat uplne nezarucuje, ze "plati". Logika je holt nejnelogictejsi oblast matematiky ;-)
Miško | org | 16. 11. 2013 00:05:51
Ja mám niečo trochu menej stredoškolské a trochu viac informatické. Jedná sa o Halting problem.
Slávna veta z teoretickej informatiky hovorí, že neexistuje program, ktorý rozhodne, či daný program na danom vstupe skončí. (Čiže vstup tohoto programu je: nejaký program , a vstup
, a vstup  pre tento program). Učene hovoríme, že neexistuje algoritmus riešiaci Halting problem.
pre tento program). Učene hovoríme, že neexistuje algoritmus riešiaci Halting problem.
Relatívne jednoduchý dôsledok tej to vety je, že neexistuje program ktorý rozhodne, či daný program skončí pre každý vstup. (Tentokrát je teda vstup iba program ).
).
A teraz príde to zaujímavé. Predstavme si na chvíľu, že by taký program existoval, nazvime ho Mlynček. Potom by sme vedeli algoritmicky rozhodnúť, či platí hypotéza prvočíselných dvojčiat! Ako? Vytvorme program ktorý na vstupe dostane číslo
ktorý na vstupe dostane číslo  , a postupne bude overovať, či čísla
, a postupne bude overovať, či čísla  sú obe prvočísla pre
sú obe prvočísla pre  . Ak by sme vedeli, že skončí pre každé
. Ak by sme vedeli, že skončí pre každé  , tak je hypotéza pravdivá, ináč neplatí.
, tak je hypotéza pravdivá, ináč neplatí.
Nie je ťažké si rozmyslieť, že podobným trikom by sme vedeli rozhodnúť o platnosti Veľkej Fermatovej vety alebo Collatzovho problému. Môžeme však úvahu posunúť o rád ďalej: ak by Mlynček existoval, vedeli by sme algoritmicky overiť platnosť každej matematickej vety!
+ skrytý text
Záver? Možno teoretická informatika má viac spoločného so základmi matematiky, než si myslíme. Možno dôkazy a algoritmy sú v skutočnosti veľmi príbuzné. Možno som len okľukou dokázal, že Mlynček nemôže existovať, pretože matematické vety nejde rozhodovať algoritmicky. A možno iba celý čas zavádzam. Či nie?
Slávna veta z teoretickej informatiky hovorí, že neexistuje program, ktorý rozhodne, či daný program na danom vstupe skončí. (Čiže vstup tohoto programu je: nejaký program
Relatívne jednoduchý dôsledok tej to vety je, že neexistuje program ktorý rozhodne, či daný program skončí pre každý vstup. (Tentokrát je teda vstup iba program
A teraz príde to zaujímavé. Predstavme si na chvíľu, že by taký program existoval, nazvime ho Mlynček. Potom by sme vedeli algoritmicky rozhodnúť, či platí hypotéza prvočíselných dvojčiat! Ako? Vytvorme program
Nie je ťažké si rozmyslieť, že podobným trikom by sme vedeli rozhodnúť o platnosti Veľkej Fermatovej vety alebo Collatzovho problému. Môžeme však úvahu posunúť o rád ďalej: ak by Mlynček existoval, vedeli by sme algoritmicky overiť platnosť každej matematickej vety!
+ skrytý text
Majme matematickú vetu  . Zostrojme program
. Zostrojme program  , na jeho vstupe nebude záležať.
, na jeho vstupe nebude záležať.  bude postupne prechádzať všetky možné dokazy -- to ide, pretože dôkaz je len konečná postupnosť písmen -- a pre každý overí, či je to dôkaz pre
bude postupne prechádzať všetky možné dokazy -- to ide, pretože dôkaz je len konečná postupnosť písmen -- a pre každý overí, či je to dôkaz pre  . Ak Mlynček povie, že
. Ak Mlynček povie, že  skončí, tak vieme, že veta platí. (Aby to celé fungovalo, musíme nejak rozumne vedieť povedať, čo je to veta, čo je to dôkaz, a musíme vedieť algoritmicky overiť správnosť dôkazu. To sa dá.)
skončí, tak vieme, že veta platí. (Aby to celé fungovalo, musíme nejak rozumne vedieť povedať, čo je to veta, čo je to dôkaz, a musíme vedieť algoritmicky overiť správnosť dôkazu. To sa dá.)
Záver? Možno teoretická informatika má viac spoločného so základmi matematiky, než si myslíme. Možno dôkazy a algoritmy sú v skutočnosti veľmi príbuzné. Možno som len okľukou dokázal, že Mlynček nemôže existovať, pretože matematické vety nejde rozhodovať algoritmicky. A možno iba celý čas zavádzam. Či nie?
E.T. | org | 9. 11. 2013 20:10:18
Ahoj,
je tu další várka hintů. (Pro všechny, kteří v anketě zvolili poslední možnost jen opakuji, že po termínu odeslání každé série se na našich stránkách objeví hinty ke všem úlohám dané série, abyste si mohli dořešit ty úlohy, které jste sami nerozlouskli. Víc toho najdete zde na matematickém chatu v příspěvku s prvními hinty.) Nyní k samotným radám:
obecná:
+ skrytý text
úloha 1:
+ skrytý text
úloha 2:
+ skrytý text
úloha 3:
+ skrytý text
úloha 4:
+ skrytý text
úloha 5:
(i)+ skrytý text
(ii)+ skrytý text
úloha 6:
(i)+ skrytý text
(ii)+ skrytý text
úloha 7:
(i)+ skrytý text
(ii)+ skrytý text
úloha 8:
(i)+ skrytý text
(ii)+ skrytý text
Přeji příjemné řešení.
pozn.: Jen připomínám, že se nás můžete zeptat na jakékoliv další hinty a my vám je rádi dáme. Můžete si radit i navzájem či zde prezentovat svá řešení, ale prosíme vás, abyste tak činili minimálně den po termínu odeslání úloh příslušné série.
@Rado (návrh na přesun hintů jinam): Možná u příštích sérií. Uvidíme. ;-)
je tu další várka hintů. (Pro všechny, kteří v anketě zvolili poslední možnost jen opakuji, že po termínu odeslání každé série se na našich stránkách objeví hinty ke všem úlohám dané série, abyste si mohli dořešit ty úlohy, které jste sami nerozlouskli. Víc toho najdete zde na matematickém chatu v příspěvku s prvními hinty.) Nyní k samotným radám:
obecná:
+ skrytý text
Přečtěte si název série a zkuste jej nějak využít při řešení. Hledejte tedy nějaké podobné trojúhelníky nebo nějaké jiné útvary.
úloha 1:
+ skrytý text
Najděte 4 čísla  taková, že
taková, že  a že trojice
a že trojice  a
a  splňují trojúhelníkovou nerovnost.
splňují trojúhelníkovou nerovnost.
úloha 2:
+ skrytý text
Ukažte že  a
a  jsou rovnoramenné a navzájem podobné. (
jsou rovnoramenné a navzájem podobné. ( je průsečík
je průsečík 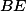 a
a  .)
.)
úloha 3:
+ skrytý text
Ukažte, že  a
a  jsou podobné. Stejně tak jsou podobné
jsou podobné. Stejně tak jsou podobné  a
a  . Navíc je koeficient podobnosti stejný.
. Navíc je koeficient podobnosti stejný.
úloha 4:
+ skrytý text
Středy úseček  po řadě označme
po řadě označme  . Ukažte, že pak čtyřúhelník
. Ukažte, že pak čtyřúhelník  je kosočtverec. Tedy, že má všechny strany stejně dlouhé a dvojice protějších stran rovnoběžné.
je kosočtverec. Tedy, že má všechny strany stejně dlouhé a dvojice protějších stran rovnoběžné.
úloha 5:
(i)+ skrytý text
Pomocí zadaných rovností úhlů najděte dvě vhodné dvojice podobných trojúhelníků.
(ii)+ skrytý text
Podobnosti zapište jako rovnosti poměrů délek stran. Tyto rovnosti vhodně upravte a sečtěte.
úloha 6:
(i)+ skrytý text
Dokažte podobnost  .
.
(ii)+ skrytý text
Dokažte podobnost  .
.
úloha 7:
(i)+ skrytý text
Zobrazte bod 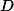 ve stejnolehlosti, která zobrazuje
ve stejnolehlosti, která zobrazuje 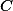 na
na  a
a  na
na 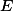 . Jeho obraz si označme
. Jeho obraz si označme  .
.
(ii)+ skrytý text
Ukažte, že čtyřúhelník  je tětivový.
je tětivový.
úloha 8:
(i)+ skrytý text
Označme středy  postupně
postupně  ,
,  . Ukažte, že
. Ukažte, že  a
a  jsou navzájem podobné.
jsou navzájem podobné.
(ii)+ skrytý text
Ukažte, že "směr" přímky  je přesně "mezi směry" přímek
je přesně "mezi směry" přímek  .
.
Přeji příjemné řešení.
pozn.: Jen připomínám, že se nás můžete zeptat na jakékoliv další hinty a my vám je rádi dáme. Můžete si radit i navzájem či zde prezentovat svá řešení, ale prosíme vás, abyste tak činili minimálně den po termínu odeslání úloh příslušné série.
@Rado (návrh na přesun hintů jinam): Možná u příštích sérií. Uvidíme. ;-)
Miroslav Olšák | org | 7. 11. 2013 02:03:45
To se vám to řeší, když umíte (narozdíl ode mně) řešit Apollionovy úlohy.
To prohazování (Problém 17) je nějak jasné :-)
+ skrytý text
Problém 18: V rovině je dáno několik bodů, každému je přiřazeno nezáporné reálné číslo nepřevyšující 1006 a navíc vzdálenost žádných dvou bodů nepřevyšuje rozdíl jejich hodnot. Ukažte, že je možné tyto body ohraničit uzavřenou křivkou délky menší než 2013.
To prohazování (Problém 17) je nějak jasné :-)
+ skrytý text
Je to n-1 prohození.
To stačí:+ skrytý text
To stačí:+ skrytý text
Prohazuji postupně sousední dvojičky zprava doleva.
a je potřeba:+ skrytý textV každém kroku posunu doprava jenom jedno číslo.
Problém 18: V rovině je dáno několik bodů, každému je přiřazeno nezáporné reálné číslo nepřevyšující 1006 a navíc vzdálenost žádných dvou bodů nepřevyšuje rozdíl jejich hodnot. Ukažte, že je možné tyto body ohraničit uzavřenou křivkou délky menší než 2013.
Josef Tkadlec | 7. 11. 2013 00:32:54
petr: Na druhý pokus jsem nápovědu pochopil. Hodně, hodně dobré :).
Tak teď co s tím BakyXovým přehazováním dvojic?
Tak teď co s tím BakyXovým přehazováním dvojic?
petr | 29. 10. 2013 19:59:08
To katka - k elipse - nápověda jak dál
+ skrytý text
+ skrytý text
Představte si kružnici se středem v tom zadaném bodě elipsy, procházející zadaným ohniskem, přidejte ty dva body, které již máte (zrcadlové obrazy ohniska podle tečen) a řeště standardní apolloniovu úlohu kružnice-bod-bod. Pochopitelně potřebujeme vnitřní dotyk.
katka | 28. 10. 2013 02:38:41
Aby sa na to celkom nezabudlo, napisem nieco k tej elipse.
Zial, zatial sa mi s tym problemom podarilo pohnut len trochu. Konkretne, prisla som na toto:
+ skrytý text
A z toho je zrejme, ze treba uz "len"
+ skrytý text
Lenze ja zatial neviem ako. Mozno to bude vediet niekto dokoncit, a mozno ma presvedcite, ze tadialto cesta nevedie :)
Zial, zatial sa mi s tym problemom podarilo pohnut len trochu. Konkretne, prisla som na toto:
+ skrytý text
Viem zostrojit priamku, na ktorej lezi druhe ohnisko (vyuzivam pri tom len tie 2 dotycnice a ohnisko, ten bod elipsy nie).
Ako na to? Dam len drobnu, trochu mysticku napovedu :)
+ skrytý text
Ako na to? Dam len drobnu, trochu mysticku napovedu :)
+ skrytý text
uhol odrazu sa rovna uhlu dopadu...
A z toho je zrejme, ze treba uz "len"
+ skrytý text
najst to druhe ohnisko pomocou toho jedneho zadaneho bodu elipsy.
Lenze ja zatial neviem ako. Mozno to bude vediet niekto dokoncit, a mozno ma presvedcite, ze tadialto cesta nevedie :)
BakyX | 27. 10. 2013 01:02:33
Super, takže:
Riešenie problému 16:
+ skrytý text
Problém 17:
Máme danú usporiadanú -ticu
-ticu  . V jednom kroku môžeme urobiť vzájomnú výmenu dvoch čísel v tejto
. V jednom kroku môžeme urobiť vzájomnú výmenu dvoch čísel v tejto  -tici. Najmenej koľko krokov potrebujeme, aby sme dosiahli
-tici. Najmenej koľko krokov potrebujeme, aby sme dosiahli  -ticu
-ticu  ?
?
Riešenie problému 16:
+ skrytý text
Pomocný odhad:
 , pretože
, pretože  .
.
Ak tak odhadneme každý člen ľavej strany a navyše použijeme , čo plynie z
, čo plynie z  , tak dostávame presne to, čo chceme.
, tak dostávame presne to, čo chceme.
Ak tak odhadneme každý člen ľavej strany a navyše použijeme
Problém 17:
Máme danú usporiadanú
Rado | 27. 10. 2013 00:22:10
Jajks. Samozřejmě jsem strašně hloupý a zapomněl jsem dopsat podmínku:  . Teď už by to snad mělo fungovat :)
. Teď už by to snad mělo fungovat :)
Xellos | 27. 10. 2013 00:06:14
Fakt. Dokonca ked a,b,c idu do nuly, tak L strana ide do nekonecna a prava do 6. Nechce to vazbu nahodou?
BakyX | 26. 10. 2013 23:33:09
Tá nerovnosť je akosi divná, napr. neplatí pre  .
.
Rado | 26. 10. 2013 16:40:27
No, elipsu neumim, ale zato umim vyřešit problém 15 (který byl nesprávně nazván jako problém 14).
Řešení problému 15: + skrytý text
Otázka k této úloze:+ skrytý text
Bonusová úloha pro zájemce na podobný princip: (její řešení sem nepište) + skrytý text
A nakonec problém 16: Pro kladná čísla ukažte nerovnost
ukažte nerovnost 
Řešení problému 15: + skrytý text
Nechť  je obraz bodu
je obraz bodu 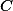 podle
podle 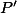 . Potom protože
. Potom protože 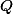 je obraz
je obraz 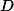 v tomto zobrazení)
v tomto zobrazení)  , takže
, takže  ,
, 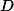 a
a  leží na přímce. Analogicky pokud definujeme
leží na přímce. Analogicky pokud definujeme  jako obraz
jako obraz  podle
podle 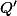 a
a 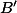 jako obraz
jako obraz  podle
podle 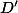 , dostaneme, že
, dostaneme, že  leží na
leží na  a
a 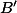 je průsečík
je průsečík  a
a  . K tomu
. K tomu  a
a  . Chceme dokázat, že
. Chceme dokázat, že  ,
,  a
a  procházejí jedním bodem.
procházejí jedním bodem.
Nyní z vlastností rovnoběžníků a sinovky: . Proto z analogických rovností dostaneme
. Proto z analogických rovností dostaneme  , čímž jsme z goniometrické Cevovky hotovi.
, čímž jsme z goniometrické Cevovky hotovi.
Q.E.D.
Nyní z vlastností rovnoběžníků a sinovky:
Q.E.D.
Otázka k této úloze:+ skrytý text
Existuje jednoduší/hezčí způsob, jak dokázat, že  ,
,  a
a  se protínají v jednom bodě? Ještě to umím analyticky po tom, co se "velký rovnoběžník" afinně narovná na obdélník, ale to je celkem hnus...
se protínají v jednom bodě? Ještě to umím analyticky po tom, co se "velký rovnoběžník" afinně narovná na obdélník, ale to je celkem hnus...
Bonusová úloha pro zájemce na podobný princip: (její řešení sem nepište) + skrytý text
Máte daný trojúhelník  a dvě přímky
a dvě přímky 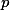 a
a 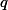 , které nejsou rovnoběžné a žádná z nich není kolmá k žádné ze stran trojúhelníka. Kolmice k
, které nejsou rovnoběžné a žádná z nich není kolmá k žádné ze stran trojúhelníka. Kolmice k 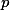 resp.
resp. 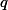 skrze
skrze  , resp.
, resp.  , resp.
, resp. 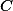 označíme postupně
označíme postupně  ,
,  ,
,  ,
,  ,
,  ,
,  . Průniky
. Průniky  ,
,  ,
,  ,
,  ,
,  ,
,  postupně s
postupně s  ,
,  ,
,  ,
,  ,
,  ,
,  označíme postupně
označíme postupně  . Dokažte, že
. Dokažte, že 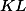 ,
, 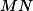 a
a  se protínají v jednom bodě.
se protínají v jednom bodě.
A nakonec problém 16: Pro kladná čísla
Alena Skálová | 21. 10. 2013 21:31:52
Není, ale to není podstatné.
Důležité je, jak se řeší elipsa. (-:
Důležité je, jak se řeší elipsa. (-:
OD | 21. 10. 2013 14:31:31
Zdravim,
je ta nejmenovana stredni skola z Brna? :-)
je ta nejmenovana stredni skola z Brna? :-)
Alena Skálová | 20. 10. 2013 23:16:07
Ahoj,
mám úlohu, kterou neumím vyřešit ani já, ani žádný matikář z nejmenované střední školy (tam jsem se o ní dozvěděla). Je ze sbírky, takže řešitelná by snad být měla... no, posuďte sami. (-:
Je dáno jedno ohnisko elipsy, její dvě tečny a jeden bod elipsy. Nalezněte druhé ohnisko (samosebou rozumí se, že synteticky).
Pokud vyřešíte, dejte řešení prosím do spoileru, ať mohou zkoušet i ostatní. A budete-li umět dobře hintit, vítám... třeba to vyřeším aspoň s nápovědou. (-:
mám úlohu, kterou neumím vyřešit ani já, ani žádný matikář z nejmenované střední školy (tam jsem se o ní dozvěděla). Je ze sbírky, takže řešitelná by snad být měla... no, posuďte sami. (-:
Je dáno jedno ohnisko elipsy, její dvě tečny a jeden bod elipsy. Nalezněte druhé ohnisko (samosebou rozumí se, že synteticky).
Pokud vyřešíte, dejte řešení prosím do spoileru, ať mohou zkoušet i ostatní. A budete-li umět dobře hintit, vítám... třeba to vyřeším aspoň s nápovědou. (-:
abstract nonsense | 19. 10. 2013 20:58:37
Reseni 14 + skrytý text
Problem 14
Nechť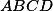 je rovnoběžník, bod
je rovnoběžník, bod  , resp.
, resp. 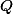 leží na přímce
leží na přímce 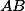 , resp.
, resp. 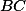 . Body
. Body 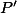 ,
, 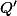 ,
, 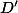 jsou po řadě středy úseček
jsou po řadě středy úseček  ,
,  ,
,  . Dokažte, že přímky
. Dokažte, že přímky  ,
,  ,
,  se protínají právě v jednom bodě.
se protínají právě v jednom bodě.
Postupujme sporem, predpokladejme



Sectenim dostaneme , z trojuhelnikove nerovnosti dostaneme
, z trojuhelnikove nerovnosti dostaneme  , tedy z tranzitivity plyne
, tedy z tranzitivity plyne

Pro je podminka ekvivalentni s
je podminka ekvivalentni s  , dosazenim dostaneme
, dosazenim dostaneme

Pro dukaz ulohy nam tedy staci dokazat

Zrejme
1) Pokud , pak zrejme plati
, pak zrejme plati  ale tahle nerovnost je ekvivalentni s kyzenou
ale tahle nerovnost je ekvivalentni s kyzenou 
2) Pokud , pak
, pak  ale to je ekvivalentni s pozadovanou nerovnosti
ale to je ekvivalentni s pozadovanou nerovnosti 
3) Pokud , pak
, pak  a to je spor.
a to je spor.
Sectenim dostaneme
Pro
Pro dukaz ulohy nam tedy staci dokazat
Zrejme
1) Pokud
2) Pokud
3) Pokud
Problem 14
Nechť
Kenny | 19. 10. 2013 13:43:07
Oprava:
Ukažte, že nějaká dvě mají absolutní hodnotu součtu větší než jedna.
Ukažte, že nějaká dvě mají absolutní hodnotu součtu větší než jedna.




