E.T. | org | 13. 2. 2014 21:19:57
Ahoj,
přichází další várka nápověd:
úloha 1:
+ skrytý text
úloha 2:
+ skrytý text
úloha 3:
+ skrytý text
úloha 4:
+ skrytý text
úloha 5:
+ skrytý text
úloha 6:
+ skrytý text
úloha 7:
+ skrytý text
úloha 8:
+ skrytý text
přichází další várka nápověd:
úloha 1:
+ skrytý text
Jaký by musel být součet oněch čísel?
úloha 2:
+ skrytý text
Každý kluk má o jednu spolužačku více než jakékoliv děvče.
úloha 3:
+ skrytý text
Následují první dva kroky správného postupu párování (to neznamená, že jiné postupy nejsou):
i)+ skrytý text
i)+ skrytý text
i)+ skrytý text
Zprůměrujme čísla 1 a 3.
i)+ skrytý text
Zprůměrujme čísla 2 a 2.
úloha 4:
+ skrytý text
Co se stane s rozdílem oněch čísel po tom, co Alča provede danou operaci?
úloha 5:
+ skrytý text
Stačí ukázat, že vždy umíme nalézt 2k dílků vedle sebe, mezi kterými je k těch větších.
+ skrytý text
+ skrytý text
Vyberme tedy nějakých 2k dílků vedle sebe. Zkusme jeden krajní dílek odebrat a jeden (na druhé straně) přidat. Jak se tím změní počet vybraných větších dílků?
úloha 6:
+ skrytý text
Nalezněte párování všech průměrných podmnožin, které mají více než jeden prvek.
+ skrytý text
+ skrytý text
Popárujte ty podmnožiny, které obsahují průměr svých členů s těmi, které ho neobsahují (ale jinak jsou stejné).
úloha 7:
+ skrytý text
Ukažte, že po každém "zpoloměrování" dvou čísel se součet převrácených hodnot všech čísel zmenší.
úloha 8:
+ skrytý text
Použijte kruhovou inverzi. (http://mks.mff.cuni.cz/library/KruhovaInverze...)
Jan Jurka | 16. 1. 2014 15:00:31
Reseni 19
+ skrytý text
Problem 20:
+ skrytý text
+ skrytý text
Sumy na obou stranach secteme a dostaneme rovnici  neboli
neboli  , tohle je hyperbola, tedy pujde zredukovat na Pellovu rovnici a opravdu muzeme psat
, tohle je hyperbola, tedy pujde zredukovat na Pellovu rovnici a opravdu muzeme psat  Tohle je Pellova rovnice se zakladnim resenim
Tohle je Pellova rovnice se zakladnim resenim  , tedy pro vsechna reseni teto rovnice plati
, tedy pro vsechna reseni teto rovnice plati


pro
Souctem techto rovnic dostaneme
 Dosazovanim za
Dosazovanim za 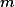 postupne dostavame posloupnost reseni
postupne dostavame posloupnost reseni  . Tedy hledane
. Tedy hledane  je
je  . A opravdu lze overit, ze
. A opravdu lze overit, ze

pro
Souctem techto rovnic dostaneme
Problem 20:
+ skrytý text
Číslo  lze zapsat jako součet dvou po sobě jdoucích čtverců a jako součet tří po sobě jdoucích čtverců
lze zapsat jako součet dvou po sobě jdoucích čtverců a jako součet tří po sobě jdoucích čtverců

Najděte nejmenší přirozené číslo větší než , které lze také zapsat jako součet dvou po sobě jdoucích čtverců a jako součet tří po sobě jdoucích čtverců. (Čtvercem rozumíme druhou mocninu přirozeného čísla.)
, které lze také zapsat jako součet dvou po sobě jdoucích čtverců a jako součet tří po sobě jdoucích čtverců. (Čtvercem rozumíme druhou mocninu přirozeného čísla.)
Najděte nejmenší přirozené číslo větší než
Josef Tkadlec | 16. 1. 2014 00:22:02
Problém 18:
+ skrytý text
Problém 19: Řekneme, že přirozené číslo je superhrubé, ak existuje
je superhrubé, ak existuje  takové, že
takové, že  Najděte nejmenší superhrubé číslo větší než 250.
Najděte nejmenší superhrubé číslo větší než 250.
+ skrytý text
Stránka Minulé ročníky v sekci Matematika skrývá mnohá tajemství: http://mks.mff.cuni.cz/archive/26/1.pdf.
Problém 19: Řekneme, že přirozené číslo
E.T. | org | 15. 1. 2014 03:33:18
Sice pozdě, ale přece...
přichází další várka nápověd! Tentokrát ke 4. podzimní sérii.
úloha 1:
+ skrytý text
úloha 2:
(i)
+ skrytý text
(ii)
+ skrytý text
úloha 3:
+ skrytý text
úloha 4:
(i)
+ skrytý text
(ii)
+ skrytý text
úloha 5:
+ skrytý text
úloha 6:
+ skrytý text
úloha 7:
+ skrytý text
úloha 8:
(i)
+ skrytý text
(ii)
+ skrytý text
Přeji příjemné řešení,
E.T.
přichází další várka nápověd! Tentokrát ke 4. podzimní sérii.
úloha 1:
+ skrytý text
Je to 13. (Nezapomeňte na ověření, že víc to být nemůže i že 13 vyhovuje.)
úloha 2:
(i)
+ skrytý text
Rozdělte kružnici na dva oblouky jejichž hranicemi jsou čísla 1 a 2014.
(ii)
+ skrytý text
Může se stát, že daný součet na jednom oblouku bude menší než 2013?
úloha 3:
+ skrytý text
Označme hledané číslo m. Pak m+1 a m+10 jsou druhé mocniny nějakých přirozených čísel (neboli čtverce). Jaký je největší čtverec takový, že po přičtení devítky opět vznikne čtverec?
úloha 4:
(i)
+ skrytý text
Ukažte, že se můžeme omezit jen na podmnožiny o maximálně třech prvcích. (viz bod (ii)) A maxima tak nabydeme, pokud vybereme všechny. (To, že tento výběr vyhovuje podmínkám zadání se ověří snadno.)
(ii)
+ skrytý text
Ukažte, že pokud by nějaká z podmnožin (pojmenujme ji A) měla více než tři prvky, pak byste ji mohli nahradit její tříprvkovou podmnožinou (tu nazvěme B). Musí totiž platit:
+ skrytý text
+ skrytý text
+ skrytý text
Množina B není v původním výběru.
+ skrytý text
Nahrazením množiny A množinou B nepokazíme ani jednu z podmínek v zadání.
úloha 5:
+ skrytý text
Označme koncové body daného oblouku X a Y. Pak ukažte, že pokud X a Y náleží různým stranám trojúhelníka ABC, je velikost úhlu XSY (a proto i daného oblouku) vždy stejná. Pokud by X, Y ležely na stejném rameni, bude dálka oblouku vždy menší... Pro jaké polohy S nastává jaký případ?
úloha 6:
+ skrytý text
Každá věž je buď "neohrožována", a pak ve stejném sloupci a řádku už žádná jiná věž není (tedy každá taková věž obsadí dvě řady), nebo se ohrožuje s jednou navzájem (pak tyto dvě věže obsazují tři řady). (Řadou rozumíme buď řádek, nebo sloupec.)
úloha 7:
+ skrytý text
Je to 7. Musíte ukázat 2 věci -- že na 7 vhodné rozmístění černých polí existuje a že na 6 (nebo méně) ne.
+ skrytý text
+ skrytý text
První část nechme k ověření vaší kreativní mysli. Druhou můžeme ukázat sporem aplikací podobných myšlenek, jako jsou tyto:
- Předpokládejme, že máme vhodné začernění 6 polí.
+ skrytý text
+ skrytý text
Podobnými úvahami po chvíli dojdete ke sporu.
- Předpokládejme, že máme vhodné začernění 6 polí.
+ skrytý text
Na šachovnici se vejde 6 křížů bez překrývání (ověřte si). Proto v každém kříži musí být 1 černé pole. V rozích šachovnice tedy nemohou být černá pole, protože neleží v žádném kříži.
+ skrytý text
Toto navíc musí platit pro všechna možná vložení šesti křížů do šachovnice a černá pole mohou být jen ta, která leží při každém vložení v nějakém kříži. (Tedy třeba celý okraj šachovnice nesmí být začerněný.)
Podobnými úvahami po chvíli dojdete ke sporu.
úloha 8:
(i)
+ skrytý text
Nejprve si formulujme pomocné lemma.
Lemma: Mějme 2k párů čísel ( ). Ty můžeme rozdělit na 2 skupiny po k dvojicích, tak, že platí:
). Ty můžeme rozdělit na 2 skupiny po k dvojicích, tak, že platí:
- Označíme-li součet všech áček v první skupině x, a ve druhé skupině y, pak absolutní hodnota rozdílu x-y je neostře menší než maximum ze všech áček.
- Označíme-li součet všech béček v první skupině m, a ve druhé skupině n, pak absolutní hodnota rozdílu m-n je neostře menší než maximum ze všech béček.
(Platí obě vlastnosti zároveň.)
Důkaz:+ skrytý text
Lemma: Mějme 2k párů čísel (
- Označíme-li součet všech áček v první skupině x, a ve druhé skupině y, pak absolutní hodnota rozdílu x-y je neostře menší než maximum ze všech áček.
- Označíme-li součet všech béček v první skupině m, a ve druhé skupině n, pak absolutní hodnota rozdílu m-n je neostře menší než maximum ze všech béček.
(Platí obě vlastnosti zároveň.)
Důkaz:+ skrytý text
Provedeme indukcí podle k. + skrytý text
Nejobtížnější je indukční krok -- indukční předpoklad použijte na 2k párů s minimálními áčky. + skrytý text
Pak první nerovnost platí, ať přidáme nové dva páry jakkoliv. Stačí vydiskutovat všechny možné případy a ukázat, že platí i druhá nerovnost.
(ii)
+ skrytý text
Vhodně použijte lemma:+ skrytý text
Odeberme dvě bedny s maximálním počtem ananasů a jablek. Pak na zbylé bedny použijte lemma, kde každá bedna je pár, a je počet jejích ananasů a b jablek.
Přeji příjemné řešení,
E.T.
Baklazan | 5. 1. 2014 13:51:16
Diki.
Miroslav Olšák | org | 5. 1. 2014 10:45:39
Ne, pouze +
Baklazan | 5. 1. 2014 00:39:17
V ulohe 7 (aktualna seria): Povazuje sa aj kriz v tvare X za Grecky?
katka | 18. 12. 2013 10:08:15
aha, uz totam vidim, vcera vecer to tam tusim este nebolo :)
katka | 18. 12. 2013 10:06:30
Ten dejepisny seminar sa mi paci, zo skoly si dejepis pamatam len ako predmet, na ktory sa stacilo namemorovat nejake fakty.
Jedna informacia mi vsak na stranke chyba, alebo som ju prehliadla: pre koho je seminar urceny? Mozu ho riesit len stredoskolaci, resp. mladsi ziaci, alebo uplne hocikto?
Jedna informacia mi vsak na stranke chyba, alebo som ju prehliadla: pre koho je seminar urceny? Mozu ho riesit len stredoskolaci, resp. mladsi ziaci, alebo uplne hocikto?
Josef Svoboda | 17. 12. 2013 22:28:07
Ahoj!
Miluješ matematiku a řešíš PraSe, a přesto máš pocit, že Ti ke spokojenému životu ještě něco chybí?
Pak je tu pro Tebe DěS!!!
Ano, je to tak! Legendární dějepisný korespondenční seminář se právě rozjíždí první sérií! Termín odeslání je již 20. ledna. Neváhej tedy a nauč se přes Vánoce něco z historie!
Vše potřebné najdeš na našich stránkách http://des.thilisar.cz
Za orgy DěSu,
Pepa S., Štěpán, Martin Č., Barča K. a další...
Miluješ matematiku a řešíš PraSe, a přesto máš pocit, že Ti ke spokojenému životu ještě něco chybí?
Pak je tu pro Tebe DěS!!!
Ano, je to tak! Legendární dějepisný korespondenční seminář se právě rozjíždí první sérií! Termín odeslání je již 20. ledna. Neváhej tedy a nauč se přes Vánoce něco z historie!
Vše potřebné najdeš na našich stránkách http://des.thilisar.cz
Za orgy DěSu,
Pepa S., Štěpán, Martin Č., Barča K. a další...
Josef Tkadlec | 13. 12. 2013 14:49:49
M: Označil bych si délku a šířku toho obdélníka (třeba 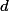 a
a  ) a z každé z prvních dvou vět bych sestavil jednu rovnici. Pak bych z jedné rovnice dosadil za jednu neznámou do té druhé a dopočítal.
) a z každé z prvních dvou vět bych sestavil jednu rovnici. Pak bych z jedné rovnice dosadil za jednu neznámou do té druhé a dopočítal.
všichni: Řešte TR KSko :) (http://iksko.org/triks/current.php). Troufnu si naznačit, že máte slušnou šanci na vítězství -- favoriti tohle kolo pokazili ;).
KSko :) (http://iksko.org/triks/current.php). Troufnu si naznačit, že máte slušnou šanci na vítězství -- favoriti tohle kolo pokazili ;).
Od 7. 11. už uplynulo docela dost času... To je vážně ten Mirkův Problém 18 tak těžký?
všichni: Řešte TR
Od 7. 11. už uplynulo docela dost času... To je vážně ten Mirkův Problém 18 tak těžký?
M | 12. 12. 2013 15:52:56
Obdelník má délku o 20 cm větší než šířku. Zmenší-li se délka o 5cm a zvětší se šířka o 10cm, zvětší se obsah obdelníku o 200cm2. Jaké jsou rozměry obdelníku??
E.T. | org | 7. 12. 2013 00:45:49
Oprava hintů ke 3. podzimní sérii:
+ skrytý text
+ skrytý text
V úloze 2 nemá být  , ale
, ale  .
.
E.T. | org | 7. 12. 2013 00:42:17
A přichází slibované hinty k 1. seriálové sérii:
1. úloha:
Postupně dokažte, že platí
(i)
+ skrytý text
(ii)
+ skrytý text pro nějaké c
pro nějaké c
(iii)
+ skrytý text
(iv)
+ skrytý text
2. úloha:
+ skrytý text
3. úloha:
+ skrytý text
1. úloha:
Postupně dokažte, že platí
(i)
+ skrytý text
(ii)
+ skrytý text
(iii)
+ skrytý text
(iv)
+ skrytý text
2. úloha:
+ skrytý text
Označme p největšího prvočíselného dělitele čísla n!+k, 1<k<=n. Pak musí nastat jeden z případů:
(i)+ skrytý text
(ii)+ skrytý text
(i)+ skrytý text
p>n a snadno ukážeme, že platí, co platit má
(ii)+ skrytý text
p<=n a pak k=n a proto platí
+ skrytý text , kde a je nějaké přirozené číslo větší než 1.
, kde a je nějaké přirozené číslo větší než 1.
+ skrytý text
+ skrytý text
+ skrytý text
Kdyby p dělilo nějaké z čísel 1,2,...,n různé od p, nemohlo by p^2 dělit n!+p.
3. úloha:
+ skrytý text
Upravte do tvaru 
 a využijte tvrzení ze seriálu.
a využijte tvrzení ze seriálu.
E.T. | org | 5. 12. 2013 01:51:08
Hola hej!
Zdravíme všechna pilná Prasátka a uveřejňujeme rady k úlohám třetí série:
úloha 1:
+ skrytý text
úloha 2:
+ skrytý text
úloha 3:
+ skrytý text
úoha 4:
+ skrytý text
úloha 5:
+ skrytý text
úloha 6:
(i):
+ skrytý text
(ii):
+ skrytý text
úloha 7:
(i):
+ skrytý text
(ii):
+ skrytý text
(iii):
+ skrytý text
úloha 8:
(i):
+ skrytý text
(ii):
+ skrytý text
(iii):
+ skrytý text
Hinty k 1. seriálové sérii se zde objeví již brzy.
Zdravíme všechna pilná Prasátka a uveřejňujeme rady k úlohám třetí série:
úloha 1:
+ skrytý text
"Vnořte absolutní hodnoty do sebe."
úloha 2:
+ skrytý text
Funkce f musí být periodická. f(2x) má periodu dvakrát kratší než f(x). Rozmyslete si, že funkce f(x^2) bude mít jinou periodu než f, jen pokud f vhodně střídá znaménko.
úloha 3:
+ skrytý text
Ukažte, že, aby bylo vyhověno zadání, musí nastat jeden z těchto dvou případů. Funkce f,g jsou obě rostoucí nebo obě klesající.
úoha 4:
+ skrytý text
Vhodným dosazováním zjistěte f(1) a f(2). Pomocí těchto hodnot a f(3) dvěma způsoby vyjádřete f(12).
úloha 5:
+ skrytý text
Označme levou stranu rovnosti v zadání L(x). Vyšetřete monotónnost funkce L (pozor, L není všude monotónní "stejně"). Pomocí toho ukažte, že rovnice může mít nejvýše jedno kladné a jedno záporné řešení.
úloha 6:
(i):
+ skrytý text
Grafem libovolné kvadratické funkce (na reálných číslech) je parabola.
(ii):
+ skrytý text
Ta je osově souměrná podle kolmice na x-ovou souřadnou osu procházející vrcholem paraboly. Tím pádem nabývá daná funkce stejných hodnot na obou ramenech.
úloha 7:
(i):
+ skrytý text
Postupujte sporem. Označme si dané funkce g,h. Pak musí platit g(x)+h(x)=f(x)=x^2. Navíc existují (z periodičnosti g,h) nenulová čísla k,c taková, že g(x+c)=g(x) a h(x+k)=h(k).
(ii):
+ skrytý text
Dosaďte do rovnosti z (i) postupně (c+k), c, k, 0.
(iii):
+ skrytý text
Pak vzniklé rovnosti vhodně sečtěte.
úloha 8:
(i):
+ skrytý text
Zaměřte se na čtveřice, v nichž v=0 a u=x+y.
(ii):
+ skrytý text
Za [x,y] dosaďte postupně [t+1,t-1], [t-1,-t], [-t,t+1]
(iii):
+ skrytý text
Výsledné rovnice sečtěte.
Hinty k 1. seriálové sérii se zde objeví již brzy.
Rozkošný a důvtipný okoun | 26. 11. 2013 22:30:12
Druhá věta o pizze je super :)
A co takhle udělat orgům to opravování trochu veselejší a příští sérii jim poslat s co nejzajímavěji nazvanými lemmátky? (Každý si určitě ve svých řešeních najde něco, co se dá nazvat pomocným tvrzením.)
Lemma lama:
Pokud někdo odešle třetí sérii bez jakéhokoliv coolově nazvaného lemma, je lama!
A slováci - Myjava není originální!
A co takhle udělat orgům to opravování trochu veselejší a příští sérii jim poslat s co nejzajímavěji nazvanými lemmátky? (Každý si určitě ve svých řešeních najde něco, co se dá nazvat pomocným tvrzením.)
Lemma lama:
Pokud někdo odešle třetí sérii bez jakéhokoliv coolově nazvaného lemma, je lama!
A slováci - Myjava není originální!
Miroslav Olšák | org | 26. 11. 2013 21:55:18
Taky pravda. Naprosto nechápu, proč pojmenovávat věty po matematicích, vždyť to nikomu nic neřekne. Navíc se typicky po matematikovi pojmenuje více vět, přičemž ani jednu z nich neobjevil :-)
Ale jsou i výjimky, když už jsme u toho jídla, máme větu o sendiči
http://en.wikipedia.org/wiki/Ham_sandwich_the...
dodatek k této větě je, že platí i když si šunku zapomenete v ledničce ;-)
Jiná věta o sendviči je dokonce z matematické analýzy, Kubo, ale ta zdaleka nemá tak fajn pohádku.
Případně máme dvě věty o pizze (především ta druhá stojí za přečtení ;-) )
http://www.wolframalpha.com/input/?i=pizza+th...
A ještě mají na wiki prima obrázek k motýlímu lemmatu z algebry
http://en.wikipedia.org/wiki/File:Butterfly_l...
Ale jsou i výjimky, když už jsme u toho jídla, máme větu o sendiči
http://en.wikipedia.org/wiki/Ham_sandwich_the...
dodatek k této větě je, že platí i když si šunku zapomenete v ledničce ;-)
Jiná věta o sendviči je dokonce z matematické analýzy, Kubo, ale ta zdaleka nemá tak fajn pohádku.
Případně máme dvě věty o pizze (především ta druhá stojí za přečtení ;-) )
http://www.wolframalpha.com/input/?i=pizza+th...
A ještě mají na wiki prima obrázek k motýlímu lemmatu z algebry
http://en.wikipedia.org/wiki/File:Butterfly_l...
Jakub Krásenský | org | 26. 11. 2013 21:30:15
Pěkné... Myslím, že kdyby se věty v matematické analýze jmenovaly takhle, učily by se mnohem lépe.
Proč Bismarckova busta? Celkově jsem nepotkal moc lidí, kteří by na stole měli bustu, ale když už, nečekal bych německého státníka. To mi přijde zajímavé.
Proč Bismarckova busta? Celkově jsem nepotkal moc lidí, kteří by na stole měli bustu, ale když už, nečekal bych německého státníka. To mi přijde zajímavé.
Kuba Svoboda | 26. 11. 2013 12:54:56
Při vymýšlení názvu mrkvovo-salámové lemma jsem měl hlad a nechtěl jsem jíst nezdravě (proto salám a mrkev) a na stole mi stojí Bismarcova busta, tedy pojmenování druhého je zřejmé.
Josef Svoboda | 24. 11. 2013 17:20:08
Ahoj OD.
Toto pojmenování je pro mě také trochu záhadou. Nicméně v matematice platí, že každý si může pojmenovat cokoliv jak se mu zlíbí. Pokud ovšem napíše, o co vlastně jde.
Mrkvovo-salámové lemma + skrytý text
Bismarckovo lemma + skrytý text
Toto pojmenování je pro mě také trochu záhadou. Nicméně v matematice platí, že každý si může pojmenovat cokoliv jak se mu zlíbí. Pokud ovšem napíše, o co vlastně jde.
Mrkvovo-salámové lemma + skrytý text
říká, že v trojúhelníku ABC dělí osa úhlu BAC stranu BC v poměru b:c. Někdy se mu také říká věta o ose úhlu: http://en.wikipedia.org/wiki/Angle_bisector_t...
Bismarckovo lemma + skrytý text
říká, že pokud D je průsečík osy úhlu BAC a kružnice opsané trojúhelníku ABC, pak 1) D je střed oblouku BC, na kterém neleží bod A, 2) pokud E (resp. F) je průsečík strany AB (resp. AC) a osy úhlu ADB (resp. ADC), pak je přímka EF rovnoběžná se stranou BC.





