Martin Hora | org | 14. 11. 2014 19:57:21
Ahoj,
druhá várka nápověd je tady.
úloha 1+ skrytý text
úloha 2+ skrytý text
úloha 3+ skrytý text
úloha 4+ skrytý text
úloha 5+ skrytý text
úloha 6+ skrytý text
úloha 7+ skrytý text
úloha 8+ skrytý text
druhá várka nápověd je tady.
úloha 1+ skrytý text
Zkuste nakreslit 6 kružnic tak, aby se každá dotýkala právě 5 dalších.
úloha 2+ skrytý text
Nemají náhodou trojúhelníky BAK a CAL nějakou pěknou vlastnost?+ skrytý text
Tu vlastnost, že splývá osa jednoho vnitřního úhlu s osou jedné strany?
úloha 3+ skrytý text
Body D´E´F´ jsou na kružnici opsané trojúhelníku DEF. Pak už jen stačí si dostatečně dlouho hrát s 6 body na kružnici, dokud nevypočítáme hledané úhly.
úloha 4+ skrytý text
Bod X musí být střed kružnice vepsané trojúhelníku BCY. Na trojúhelníku BCY si označme body dotyku s jemu vepsanou kružnicí. Co pak platí pro rozdíl |XC| - |YB|?
úloha 5+ skrytý text
Kružnice se dotýkají ,právě tehdy když je součet jejich poloměrů roven vzdálenosti jejich středů. Jaké mají kružnice nad stranami BC a DA poloměry? A jak daleko jsou od sebe jejich středy?
úloha 6+ skrytý text
Zkuste důkaz sporem. Předpokládejte, že a + b > n. Mezi body Xa a Xb leží jedině bod Xn. Posuneme-li se z bodu Xb po směru hodinových ručiček o (n-b)x tak skončíme bodě Xn - mezi body Xa a Xb. Co se stane posuneme-li se z bodu Xa o (n-b)x proti směru hodinových ručiček?
úloha 7+ skrytý text
Zkoumejte úhel, který svírá společná tečna dvou po sobě následujících kružnic se stranami trojúhelníka.
úloha 8+ skrytý text
Vysledek je 5/3 pi. Můžete se pokusit dokázat, že pro libovolnou větší délku to nejde a pro libivolnou menší to lze nakreslit. A nebo můžete počkat na vzorové řešení :).
Pro důkaz maximality x je výhodné uvažovat průsečíky 3 hlavních kružnic na sféře a zkoumat jejich vzdálenosti.
Pro důkaz toho, že pro libovolnou kratší délku lze kružnice na sféru nakreslit je potřeba najít vhodné rozestavení kružnic a dokázat, že toto rozestavení splňuje zadání.
Pro důkaz maximality x je výhodné uvažovat průsečíky 3 hlavních kružnic na sféře a zkoumat jejich vzdálenosti.
Pro důkaz toho, že pro libovolnou kratší délku lze kružnice na sféru nakreslit je potřeba najít vhodné rozestavení kružnic a dokázat, že toto rozestavení splňuje zadání.
Martin Hora | org | 11. 10. 2014 13:49:37
Ahoj,
přichází první várka nápověd. Pokud jste nějakou úlohu nevyřešili a nechce se vám čekat na vzoráky, tak je následující příspěvek právě pro vás.
úloha 1+ skrytý text
úloha 2+ skrytý text
úloha 3+ skrytý text
úloha 4+ skrytý text
úloha 5+ skrytý text
úloha 6+ skrytý text
úloha 7+ skrytý text
úloha 8+ skrytý text
přichází první várka nápověd. Pokud jste nějakou úlohu nevyřešili a nechce se vám čekat na vzoráky, tak je následující příspěvek právě pro vás.
úloha 1+ skrytý text
Experimentujte, dokud nenaleznete vyhovující obarvení.+ skrytý text
Ve vyhovujícím obarvení je 12 políček vybarveno stejnou barvou.
úloha 2+ skrytý text
Páry tulipánů si můžeme rozdělit na 2 druhy. Různobarevné (jeden z páru je žlutý a druhý červený) a stejnobarevné (Oba jsou žluté, nebo jsou oba červené).
Různobarevné:+ skrytý text
Stejnobarevné:+ skrytý text
Různobarevné:+ skrytý text
Rozmyslete si, že pro každý různobarevný pár je vzdálenost žlutého tulipánu od A stejná jako vzdálenost červeného tulipánu od B.
Stejnobarevné:+ skrytý text
Zde si rozmyslete, že pokud je celkem červených i žlutých tulipánů stejný počet, tak musí být i stejný počet stejnobarevných párů s červenými tulipány a stejnobarevných párů se žlutými tulipány.+ skrytý text
Dále si rozmyslete, že pro každý pár tulipánů, platí, že součet vzdáleností obou tulipánů od A je rovna součtu vzdáleností obou tulipánů od B + skrytý text
je rovna vzdálenosti bodů A a B.
úloha 3+ skrytý text
Počet bonbónů v krabičkách je různý, takže je lze podle toho seřadit. V první krabičce je nejméně bonbónů, v druhé je druhý nejmenší počet bonbónů, ..., v desáté krabičce je nejvíce bonbónů.
Rozmyslete si, že když žádná krabička není prázdná, tak v i-té krabičce je alespoň i bonbónů.+ skrytý text
Rozmyslete si, že když žádná krabička není prázdná, tak v i-té krabičce je alespoň i bonbónů.+ skrytý text
Z první krabičky si tedy mohu vybrat bonbón nějaké barvy a z každé další krabičky si mohu vybrat bonbón barvy, kterou jsem dosud z předchozích krabiček nevybral.
úloha 4+ skrytý text
Úlohu si rozdělme na 2 případy.
1) Žádný sloupeček/řádka (Závisí na úhlu pohledu. Já tím myslím to kratší se třemi políčky) není obarven jednou barvou.+ skrytý text
2) Existuje sloupeček/řádka, která je celá obarvena jednou barvou. Bez újmy na obecnosti můžeme předpokládat, že je celý sloupeček/řádka černý/černá.+ skrytý text
1) Žádný sloupeček/řádka (Závisí na úhlu pohledu. Já tím myslím to kratší se třemi políčky) není obarven jednou barvou.+ skrytý text
Kolika různými způsoby je možno obarvit 3 políčka dvěma barvami tak, aby nebyla všechna políčka obarvená stejnou barvou? A kolik má tabulka řádek/sloupců?
2) Existuje sloupeček/řádka, která je celá obarvena jednou barvou. Bez újmy na obecnosti můžeme předpokládat, že je celý sloupeček/řádka černý/černá.+ skrytý text
Kolika různými způsoby je pak možno obarvit 3 políčka dvěma barvami tak, aby současně nebyla 2 políčka sloupečku/řádky obarvená černě? A kolik nám zbývá sloupečků/řádek k obarvení?
úloha 5+ skrytý text
Nejprve učiníme spodní odhad počtu barev.+ skrytý text
Dále dokážeme, že nám tolik barev opravdu stačí. K tomu stačí pro každé n provést konstrukci, která vyhovuje zadání.+ skrytý text
Z každého města vede n-1 různobarevných cest a každé město má navíc také vlastní barvu, která je odlišná od barev cest, jež do něj vedou. Minimálně tedy potřebujeme n různých barev.
Dále dokážeme, že nám tolik barev opravdu stačí. K tomu stačí pro každé n provést konstrukci, která vyhovuje zadání.+ skrytý text
Například si města očíslujeme 1 až n a zakreslíme je v tomto pořadí na kružnici, tak aby vytvořily pravidelný n-úhelník. Dále každá 2 města spojíme úsečkou. Nyní rozlišíme 2 případy.
1) n je sudé+ skrytý text
2) n je liché+ skrytý text
1) n je sudé+ skrytý text
V tomto případě obarvíme všechna města jednou barvou (například barvou 1). Všechny úsečky, které jsou vzájemně rovnoběžné také jednou barvou (jednou z barev 2 až n). Každý pár různoběžných úseček je obarven 2 různými barvami. Rozmyslete si, že takto obarvíme všechny úsečky a že nám k nakreslení plánku tímto způsobem stačí opravdu n barev.
2) n je liché+ skrytý text
V tomto případě opět obarvíme všechny úsečky, které jsou vzájemně rovnoběžné jednou barvou (jednou z barev 1 až n). Každý pár různoběžných úseček je obarven 2 různými barvami. Do každého města vede n-1 různobarevnch cest, takže nám na každé město zbývá jedna barva, kterou ho můžeme obarvit. V tomto případě budou mít všechna města různé barvy. Opět si rozmyslete, že tento postup obarvování splňuje zadání.
úloha 6+ skrytý text
Správná odpověď je, že se může uvolnit maximálně 44 políček. Důkaz má 2 části.
1) Najít 20 políček šachovnice takových, že se na ně mohou přesunout všechny berušky. Zkuste si takových 20 políček najít. 44 políček pak zůstane volných.
2) Dokázat, že na méně než 20 políček se všechny berušky nemohou dostat.+ skrytý text
1) Najít 20 políček šachovnice takových, že se na ně mohou přesunout všechny berušky. Zkuste si takových 20 políček najít. 44 políček pak zůstane volných.
2) Dokázat, že na méně než 20 políček se všechny berušky nemohou dostat.+ skrytý text
Můžeme obarvit modře 40 políček šachovnice tak, aby každé políčko sousedilo právě se dvěma modrými políčky. Opět si zkuste takovéto obarvení šachovnice najít.+ skrytý text
Na každé políčko se tak můžou přesunout maximálně 2 berušky z modrých polí. Tedy všechny berušky z modrých polí skončí po přesunu na nejméně 20 různých políčcích. Z toho plyne, že méně než 20 políček nám nestačí.
úloha 7+ skrytý text
Nejprve uvažujme situaci, kde se neprotínají žádné 2 stejnobarevné úsečky.+ skrytý text
Dále se podívejme na případy, kde se nějaké 2 stejnobarevné úsečky protínají.+ skrytý text
Pak každá modrá úsečka pak dělí kružnici na 2 části takové, že každá obsahuje sudý počet modrých bodů a lichý počet červených bodů.+ skrytý text
Červené body se v každé z částí nemohou všechny vzájemně popárovat, a tak musí existovat alespoň jedna červená úsečka, která protíná vybranou modrou úsečku. Na každé modré úsečce je tedy alespoň jeden fialový bod. A modrých úseček je n.
Dále se podívejme na případy, kde se nějaké 2 stejnobarevné úsečky protínají.+ skrytý text
Uvažujme, že se dvě stejnobarevné úsečky AC a BD protínají. Body A, B, C a D leží na kružnici v tomto pořadí. Rozmyslete si, že pokud tyto úsečky nahradím úsečkami AB a CD, tak se počet fialových bodů nezvětší a ani počet průsečíků stejnobarevných úseček se nezvětší.+ skrytý text
Dále si můžete rozmyslet, že každou situaci umíme převést na předchozí případ, kde se stejnobarevné úsečky neprotínají. Při tomto převodu se počet fialových bodů nezvětší, takže každá situace obsahuje alespoň n fialových bodů.
úloha 8+ skrytý text
Celou hru si nejprve zkuste s menším počtem puntíků. (S jedním, se dvěma, ...) V těchto případech vždy může Karkulka vyhrát. Z toho můžeme předpokládat a pokusit se dokázat, že tuto hru může vždy vyhrát Karkulka.
Označíme 100 tahů jako kolo. Nyní bude naším úkolem najít strategii Karkulky takovou, že se při každém kole přiblíží vítězství, dokud nakonec nevyhraje.
Takovou strategii je například následující:+ skrytý text
A proč tato strategie funguje?+ skrytý text
Označíme 100 tahů jako kolo. Nyní bude naším úkolem najít strategii Karkulky takovou, že se při každém kole přiblíží vítězství, dokud nakonec nevyhraje.
Takovou strategii je například následující:+ skrytý text
Dokud v tomto kole nenamaloval vlk modrý puntík, tak Karkulka namaluje červený puntík. V opačném případě namaluje Karkulka puntík modrý.
A proč tato strategie funguje?+ skrytý text
Uvědomme si, že nezahraje-li vlk v nějakém kole žádný modrý puntík, tak Karkulka v tomto kole vyhraje. To znamená, že pokud nechce vlk prohrát, tak musí každé kolo změnit jeden z červených puntíků na modrý.+ skrytý text
Před začátkem každého kola budeme počítat hodnotu hry. Každému puntíku přiřadíme nějakou váhu. Prvnímu puntíku dáme váhu 1, druhému 2, třetímu 4, ... a poslednímu stému 2 na 99. Jako hodnotu hry označíme součet váh červených políček. + skrytý text
Nyní si můžeme rozmyslet, že po každém kole Karkulka buď vyhraje, nebo se hodnota hry zmenší. Hodnota hry je ale vždy nezáporné celé číslo, a tak může klesnout jen konečněkrát. Bude-li se vlk bránit všemi silami, tak nakonec nastane situace, kdy bude hodnota hry bude rovna nule. Všechna políčka budou mordá a ty Karkulka může všechna přebarvit na červeno a vyhrát.
David Hruška | org | 30. 9. 2014 00:52:22
Ahoj,
právě začala první soutěž TriKS v tomto školním roce! Její zadání i obecnější informace naleznete na http://iksko.org/triks.
právě začala první soutěž TriKS v tomto školním roce! Její zadání i obecnější informace naleznete na http://iksko.org/triks.
David Hruška | org | 14. 9. 2014 23:51:10
Ahoj,
do termínu odeslání 3. série iKS (http://iksko.org/) zbývá ještě 8 dní, tak neváhejte, něco vyřešte a uspějte tak v mezinárodní konkurenci!
do termínu odeslání 3. série iKS (http://iksko.org/) zbývá ještě 8 dní, tak neváhejte, něco vyřešte a uspějte tak v mezinárodní konkurenci!
Tonda | 6. 7. 2014 15:13:29
Ahoj,
omlouvám se všem řešitelům iKSka, protože v zadání třetí úlohy má být místo
místo  . Jsem rád, že někteří chybu v zadání objevili,a pak odhadli a řešili správné řešení.
. Jsem rád, že někteří chybu v zadání objevili,a pak odhadli a řešili správné řešení.
Tonda
Tonda
omlouvám se všem řešitelům iKSka, protože v zadání třetí úlohy má být
Tonda
Tonda
Štěpán Šimsa | org | 1. 7. 2014 08:12:12
Ahoj!
Přinášíme vynikající zprávy všem příznivcům MO! Na http://iksko.org/triks/current.php si (po registraci) můžete vyzkoušet jeden IMO den nanečisto. Soutěžit můžete kdykoli od úterního poledne až do nedělní půlnoci. Máte 4,5 hodiny na vyřešení tří úloh. Za každou můžete získat až 7 bodů. Já budu také soutěžit, tak máte ideální příležitost mě porazit ;).
za iKSko,
Štěpán
Přinášíme vynikající zprávy všem příznivcům MO! Na http://iksko.org/triks/current.php si (po registraci) můžete vyzkoušet jeden IMO den nanečisto. Soutěžit můžete kdykoli od úterního poledne až do nedělní půlnoci. Máte 4,5 hodiny na vyřešení tří úloh. Za každou můžete získat až 7 bodů. Já budu také soutěžit, tak máte ideální příležitost mě porazit ;).
za iKSko,
Štěpán
Honza Jurka | 10. 6. 2014 00:37:23
Ahoj, povedlo se mi objevit něco zajímavého a rád bych se o to podělil, zbytek textu skryju, aby to nezabíralo moc místa.
+ skrytý text
+ skrytý text
Určitě mnoho z vás zná nerovnost ze zahájení 58. MO. S touhle nerovností jsem dnes zkoušel spoustu věcí, různé zobecnění, či zostření, no na žádné zobecnění jsem nepřišel, ale povedlo se mi najít (a dokázat) ostřejší nerovnost ze které nerovnost ze zahájení 58. MO ihned plyne, ta ostřejší nerovnost je, že pro všechna  platí
platí 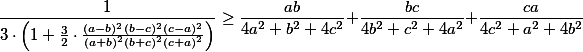
No proč to vůbec píšu? Ze dvou důvodů. Rád bych se zeptal zda někdo neví jestli se jedná o nerovnost již známou, nebo je to "originální" nerovnost. A také tahle ostřejší nerovnost nabízí zajímavý problém, ono totiž ten koeficient nejspíš není nejoptimálnější (nejmaximálnější), takže si můžeme klást následující otázku: Jaká je maximální hodnota
nejspíš není nejoptimálnější (nejmaximálnější), takže si můžeme klást následující otázku: Jaká je maximální hodnota  taková, že pro všechny kladné
taková, že pro všechny kladné  platí
platí 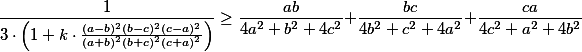
?
Například již pro nerovnost neplatí pro
nerovnost neplatí pro  ,
,  ,
,  , no takže víme
, no takže víme  .
.
No proč to vůbec píšu? Ze dvou důvodů. Rád bych se zeptal zda někdo neví jestli se jedná o nerovnost již známou, nebo je to "originální" nerovnost. A také tahle ostřejší nerovnost nabízí zajímavý problém, ono totiž ten koeficient
?
Například již pro
Ondra | 21. 5. 2014 21:09:32
Temi orientacemi se asi budu muset prokousat, (ale to je muj problem :) .
Dik za pomoc.
Dik za pomoc.
Rado | 21. 5. 2014 20:50:39
No, nejjednodušší je samozřejmě prohlásit "to je Miguelův bod", ale protože to asi nechceš (a protože si nejsem jistý, jak se píše Miguelův), tak druhé nejjednodušší řešení asi bude prostě to vyúhlit s orientovanými úhly (http://mks.mff.cuni.cz/library/OrientovaneUhl...). Detailně : necháš třeba kružnice  a
a  protnout v
protnout v 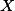 a úhlíš :
a úhlíš :  a to už je ono :)
a to už je ono :)
Ondra | 21. 5. 2014 19:48:01
Zdravim, potreboval bych poradit s dukazem toho tvrzeni:
Na primkach BC, CA, AB urcenymi stranami trojhuelniku ABC lezi postupne body P, Q, R. Dokazte, ze se kruznice (AQR), (BPR) a (CPQ) protinaji v jenom bode.
Jde mi hlavne o to, abych nemusel rozebirat kazdy pripad zvlast.
Jak teda na to?
Na primkach BC, CA, AB urcenymi stranami trojhuelniku ABC lezi postupne body P, Q, R. Dokazte, ze se kruznice (AQR), (BPR) a (CPQ) protinaji v jenom bode.
Jde mi hlavne o to, abych nemusel rozebirat kazdy pripad zvlast.
Jak teda na to?
Jan Jurka | 27. 4. 2014 17:53:28
Zdarec, překládá se to jako "okruh kvadratických celých čísel".
Matěj | 27. 4. 2014 12:33:38
Ahoj, píšu seminárku a potřeboval bych poradit s terminologií - nevíte, jak se do češtiny překládá "quadratic integer ring"? Kvadratický okruh?
Josef Svoboda | 14. 4. 2014 20:31:59
Ahoj! Také přichází nápovědy k seriálu, pěkně si je užijte:
úloha 1
+ skrytý text
úloha 2
+ skrytý text
úloha 3
+ skrytý text
úloha 1
+ skrytý text
Úlohu si rozděl na případ, kdy je n čtvercové (těžký) a kdy je bezčtvercové (snadný). + skrytý text
Rozlož si n na prvočísla. Jak přispějí ty, které jsou jen v první mocnině? + skrytý text
Čtvercoví dělitelé nepřispívají. Ostatní dělitelé se dají sečíst na nulu podobně jako v seriálu.
úloha 2
+ skrytý text
Obě strany jsou multiplikativní (z úvah o konvoluci).+ skrytý text
Rovnost tedy stačí ověřit pro mocniny prvočísel. Na to se hodí vzoreček ze zadání.
úloha 3
+ skrytý text
Zkus se zamyslet nad aritmetickou funkcí, která je multiplikativní, a přitom přiřazuje jen hodnoty 0,1,-1 podle zbytku po dělení čtyřmi. + skrytý text
Stačí nahlédnout, jak je to se sumární funkcí funkce z předchozí nápovědy.
E.T. | org | 14. 4. 2014 03:51:06
A přichází další nápovědy:
úloha 1.
+ skrytý text
úloha 2.
+ skrytý text
úloha 3.
+ skrytý text
úloha 4.
+ skrytý text
+ skrytý text
úloha 5.
+ skrytý text
úloha 6.
+ skrytý text
+ skrytý text
úloha 7.
+ skrytý text
+ skrytý text
+ skrytý text
+ skrytý text
úloha 8.
+ skrytý text
+ skrytý text
Nápovědy k seriálu se objeví velmi brzy, snad již v průběhu dneška.
Tak pilně řešte,
E.T.
úloha 1.
+ skrytý text
Tohle snad zvládnete sami :). Pokud ne, zkuste při standardním označení krychle obarvit vrcholy A,B,F,G červeně a zbylé zeleně.
úloha 2.
+ skrytý text
Nakreslete si, jak situace vypadá \uv{shora} (tedy po kolmém promítnutí do podstavy). Vrchol bude někde, kde se mohou protínat obě stěny kolmé na podstavu.
úloha 3.
+ skrytý text
Rozdělte krychle do dvou trojic a v každé trojici je poskládejte tak, aby se každá dotýkala každé nějakou stěnou. Pokud jsou krychle stejné, bude výsledný tvar trošku podobný písmenu T. Poté na sebe tato dvě \uv{téčka} vhodně položte.
úloha 4.
+ skrytý text
Ukažte, že platí jistá 3D varianta trojúhelníkové nerovnosti, tedy že obsahy tří libovolných stran čtyřstěnu mají dohromady větší obsah než strana poslední.
+ skrytý text
+ skrytý text
Promítněte si tři stěny do roviny té čtvrté.
+ skrytý text
V jakém poměru musí být podle zadání obsahy stěn?
úloha 5.
+ skrytý text
Rozšiřte levou stranu dvěma. Předpokládejme, že A,B, jsou vrcholy na hraně délky a a O střed koule opsané.
+ skrytý text
+ skrytý text
+ skrytý text
Co říká trojúhelník ABO vztahu čitatelů v upravené nerovnosti?
+ skrytý text
Co můžete říct o jmenovatelích, když víte, že koule vepsaná je celým svým objemem v čtyřstěnu?
úloha 6.
+ skrytý text
Všimněte si, že každá budova dá Davidovi nějaký interval, jak vysoká může být jeho budova, aby se nestínili.
+ skrytý text
Ukažte, že všechny intervaly mají neprázdný průnik. K tomu stačí, aby každé dva měly neprázdný průnik.
+ skrytý text
+ skrytý text
Pro spor předpokládejte, že intervaly náležící budovám A a B, mají prázdný průnik. Pak můžete dvěma způsoby odhadnout vzdálenost mezi nimi a získat spor.
úloha 7.
+ skrytý text
Označte po řadě G,H body dotyků koule vepsané s ABC a BCD a I, J body dotyků koule připsané s těmito stranami. Pozorování, že délky tětivy od daného bodu k dané kouli jsou stejně dlouhé, vám dá spoustu rovností délek různých úseček.
+ skrytý text
Ukažte, že BGI a BHJ jsou shodné.
+ skrytý text
+ skrytý text
Stačí vám |GI|=|HJ|. K tomu vám stačí ukázat, že D,G,I leží na jedné přímce a D,H,J také.
+ skrytý text
+ skrytý text
tip: Zaměřte se na stejnolehlost zobrazující kouli vepsanou na připsanou.
+ skrytý text
Nyní sklopte trojúhelníky BGI a BHJ do roviny ABC po řadě podle os AB, BC.
+ skrytý text
Nyní sklopte trojúhelníky BGI a BHJ do roviny ABC po řadě podle os AB, BC.
úloha 8.
+ skrytý text
Počítejte s objemy:
+ skrytý text
+ skrytý text
+ skrytý text
Ukažte, že poměr objemů VAiAjAk a VBiBjBk je pro libovolná i,j,k z {1,2,...,n} konstantní. Tento poměr si označme t.
+ skrytý text
+ skrytý text
(rada: Rovná se poměru objemů VA1A2...An a VB1B2...Bn.)
+ skrytý text
Nyní ukažte, že objem VAiAjAk je ai*aj*ak-krát větší než objem VBiBjBk, kde ai je poměr |Ai| a |Bi|.
+ skrytý text
+ skrytý text
(rada: Na jehlan VAiAjAk se dívejte, jako by měl podstavu VAiAj a vrchol Ak a tím ukaže , že objem VAiAjAk je ak-krát větší než objem VAiAjBk.)
+ skrytý text
Ukazte, ze vsechna ai jsou stejna, a dokoncete tak dukaz
Nápovědy k seriálu se objeví velmi brzy, snad již v průběhu dneška.
Tak pilně řešte,
E.T.
E.T. | org | 17. 3. 2014 03:07:42
A zde je slíbená nápověda:
úloha 8.
+ skrytý text
úloha 8.
+ skrytý text
Označme n stupeň polynomu P. Úlohu rozdělte na tato tři případy: P je konstantí, n=1, n>=2.
druhý případ:+ skrytý text
třetí případ:
i)+ skrytý text
ii)+ skrytý text
druhý případ:+ skrytý text
Ukažte, že zadání je vyhověno právě tehdy když jsou oba koeficienty polynomu racionální.
třetí případ:
i)+ skrytý text
Ukažte, že polynom musí mít racionální koeficienty; BÚNO celočíselné.
ii)+ skrytý text
Odhalte spor podobného typu jako ve větě o racionálních kořenech: http://en.wikipedia.org/wiki/Rational_root_th...
E.T. | org | 14. 3. 2014 20:14:03
Hola hej,
přichází další várka nápověd!
úloha 1.
+ skrytý text
úloha 2.
+ skrytý text
úloha 3.
+ skrytý text
úloha 4:
+ skrytý text
úloha 5:
+ skrytý text
úloha 6:
+ skrytý text
úloha 7.
+ skrytý text
Nápověda k osmé úloze přijde již brzy. Těšte se.
E.T.
přichází další várka nápověd!
úloha 1.
+ skrytý text
Napište např. do prvního řádku 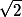 a
a  . Následně tabulku doplňte tak, aby všechny součty byly nulové.
. Následně tabulku doplňte tak, aby všechny součty byly nulové.
úloha 2.
+ skrytý text
Ne. Označme si daná čísla a, b, c. Je 2(a+b+c) racionální, nebo iracionální?
úloha 3.
+ skrytý text
Napište si na papír nějaké náhodné reálné číslo (třeba 3,84659765813...). (To bude vaše x ze zadání.) A pak sledujte, co se s ním děje, pokud ho násobíte mocninami deseti a z výsledku berete celou část.
úloha 4:
+ skrytý text
Zkuste dané podmnožiny nějak popárovat:
+ skrytý text
+ skrytý text
Do páru vždy dejte nějakou podmnožinu a její doplněk.
úloha 5:
+ skrytý text
Umocněte  na druhou a ukažte, že toto číslo je dělitelné dvěma, ale ne čtyřmi.
na druhou a ukažte, že toto číslo je dělitelné dvěma, ale ne čtyřmi.
úloha 6:
+ skrytý text
Ne. Postupujte sporem:
+ skrytý text
+ skrytý text
Je-li Filipovo číslo racionální, musí se v jeho zápise nuly "pravidelně opakovat". Přitom nuly jsou v jeho čísle na stejných pozicích, jako v Pepově čísle.
úloha 7.
+ skrytý text
Ano.
+ skrytý text
+ skrytý text
+ skrytý text
Zapište čísla a, b, c ve dvojkové soustavě.
+ skrytý text
Najděte taková desetinné zápisy, aby ani jeden z nich nebo periodický nebo ukončený a aby na každé pozici mělo právě jedno z čísel jedničku (a zbylé nuly). Ukažte, že taková čísla vyhovují zadání.
Nápověda k osmé úloze přijde již brzy. Těšte se.
E.T.
E.T. | org | 10. 3. 2014 03:30:14
Ahoj Petře,
běžně posíláme dvě až tři série naráz, ale víc zpravidla ne. Druhou a třetí podzimní sérii spolu s první seriálovou jsme posílali už v lednu, takže jsi je rozhodně měl dostat. 4.podzimní a 1.jarní sérii jsme posílali před pár dny, takže bys je měl dostat velmi brzy. Vynasnažíme se zjistit, proč Ti obálka v pořádku nedorazila, a pokud to bude v našich silách, nějak to napravit.
E.T.
běžně posíláme dvě až tři série naráz, ale víc zpravidla ne. Druhou a třetí podzimní sérii spolu s první seriálovou jsme posílali už v lednu, takže jsi je rozhodně měl dostat. 4.podzimní a 1.jarní sérii jsme posílali před pár dny, takže bys je měl dostat velmi brzy. Vynasnažíme se zjistit, proč Ti obálka v pořádku nedorazila, a pokud to bude v našich silách, nějak to napravit.
E.T.
Petr Jakubčík | 9. 3. 2014 18:19:29
Ahoj!
Chtěl bych se zeptat, jak často se posílají zpátky opravená řešení. Já jsem totiž dostal jenom ta z první podzimní série a od té doby nic. Je chyba na mé straně, nebo je to tak u MKS běžné, že se posílají opravená řešení hromadně za více sérií najednou? Díky za odpověď!
Chtěl bych se zeptat, jak často se posílají zpátky opravená řešení. Já jsem totiž dostal jenom ta z první podzimní série a od té doby nic. Je chyba na mé straně, nebo je to tak u MKS běžné, že se posílají opravená řešení hromadně za více sérií najednou? Díky za odpověď!
David Hruška | org | 7. 3. 2014 23:28:51
Ahoj,
přiblížilo se nám celostátní kolo MO (23.3. - 26.3.2014) a je tady skvělá příležitost, jak správně doladit formu
a zkusit si celostátko nanečisto! Příští týden bude probíhat v souteži TRiKS (http://iksko.org/triks/) zkrácená standardní soutěž. Ten další týden se bude od pondělka do středy soutěžit v řešení trojce úloh odpovídajících prvnímu dni na celostátku, od čtvrtka do soboty se pojede druhý den. Tak ukažte, co ve vás je a kdo budou letošní favorité! A pak hurá do Ostravy, budeme držet palce!
přiblížilo se nám celostátní kolo MO (23.3. - 26.3.2014) a je tady skvělá příležitost, jak správně doladit formu
a zkusit si celostátko nanečisto! Příští týden bude probíhat v souteži TRiKS (http://iksko.org/triks/) zkrácená standardní soutěž. Ten další týden se bude od pondělka do středy soutěžit v řešení trojce úloh odpovídajících prvnímu dni na celostátku, od čtvrtka do soboty se pojede druhý den. Tak ukažte, co ve vás je a kdo budou letošní favorité! A pak hurá do Ostravy, budeme držet palce!
David Hruška | org | 28. 2. 2014 00:15:49
Pozor, pozor!
V zadání (http://mks.mff.cuni.cz/commentary/aktualni.php) páté úlohy aktuální série jsme opomněli dodatečný předpoklad, a sice, že jsou kladná reálná čísla. Naše společnost se Vám tímto omlouvá za způsobené nepříjemnosti.
jsou kladná reálná čísla. Naše společnost se Vám tímto omlouvá za způsobené nepříjemnosti.
V zadání (http://mks.mff.cuni.cz/commentary/aktualni.php) páté úlohy aktuální série jsme opomněli dodatečný předpoklad, a sice, že