Miroslav Olšák | org | 29. 8. 2015 19:54:35
Ahoj, pro řešení první série není třeba žádná zvláštní teorie, hlavně umět dobře uvažovat a mít dobré nápady ;-) Univerzální textík napříč ročníky a sériemi (spíše pro začátečníky) je: http://mks.mff.cuni.cz/info/Jak.pdf
Někdy (což teď není případ první série) je k sérii ještě stručný doplňující text toho, co pokročilí řešitelé typicky znají, ale ostatním může pomoci. Obecný seznam sérií, textů k nim, případně i vzorových řešení je na stránce aktuálního ročníku ( http://mks.mff.cuni.cz/commentary/commentary.php ). Zatím jsme ale tuto stránku neaktualizovali na současný ročník.
A nakonec (asi to myslel Wanderer) tu bude seriál. Letošní seriál bude na téma "Do nekonečna a ještě dál". Seriál se zaobírá méně známou teorií než běžné série, takže je jeho doprovodný text výrazně delší. Seriál má tři navazující díly -- tři série a tři příslušné doprovodné texty.
Někdy (což teď není případ první série) je k sérii ještě stručný doplňující text toho, co pokročilí řešitelé typicky znají, ale ostatním může pomoci. Obecný seznam sérií, textů k nim, případně i vzorových řešení je na stránce aktuálního ročníku ( http://mks.mff.cuni.cz/commentary/commentary.php ). Zatím jsme ale tuto stránku neaktualizovali na současný ročník.
A nakonec (asi to myslel Wanderer) tu bude seriál. Letošní seriál bude na téma "Do nekonečna a ještě dál". Seriál se zaobírá méně známou teorií než běžné série, takže je jeho doprovodný text výrazně delší. Seriál má tři navazující díly -- tři série a tři příslušné doprovodné texty.
Wanderer | 26. 8. 2015 20:15:47
Jediná věc, o níž vím, je sepsaný jakýsi seminář, kterých je tu nejspíš víc, a na který byl odkaz v podzimním zadání...
Sh4rP EYE | 20. 8. 2015 15:27:26
Ahoj, mám jen jednu takovou krátkou otázku. Je tady na stránkách nějaký odkaz na doporučenou teorii (nebo něco podobného), kterou je nutné znát k vyřešení aktualního zadání PraSete? Mám namysli nějaké teorémy, vzorce a podobně.
Vejtek | 3. 8. 2015 00:36:32
Řešení 4. úlohy: + skrytý text
Úloha 5. + skrytý text
Nakreslíme si grafy funkcí  a
a 
a všimneme si, že hledáme některá řešení soustavy

Odečteme a upravíme na . Nulovost první závorky
. Nulovost první závorky
vede na kvadratickou rovnici s řešením
s řešením  , nulovost druhé závorky vede na rovnici
, nulovost druhé závorky vede na rovnici  s kořeny
s kořeny  . Mrknutím na původní obrázek vidíme, že řešením úlohy jsou čísla
. Mrknutím na původní obrázek vidíme, že řešením úlohy jsou čísla  a
a  .
.
a všimneme si, že hledáme některá řešení soustavy
Odečteme a upravíme na
vede na kvadratickou rovnici
Úloha 5. + skrytý text
Nalezněte všechny funkce  splňující
splňující
 a
a  pro všechna nenulová
pro všechna nenulová  .
.
Tonda Le | org | 3. 7. 2015 06:00:50
Ahoj,
také chci přispět k maratonu.
Řešení 3.úlohy+ skrytý text
Zadání 4. úlohy:+ skrytý text
také chci přispět k maratonu.
Řešení 3.úlohy+ skrytý text
Uvažujme  Švrčkovy body oproti vrcholům
Švrčkovy body oproti vrcholům  . Snadno vyúhlíme, že
. Snadno vyúhlíme, že  je kolmá na
je kolmá na 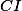 , a proto
, a proto  . Analogicky odvodíme dvě další podobné rovnoběžnosti, tudíž
. Analogicky odvodíme dvě další podobné rovnoběžnosti, tudíž  a
a  jsou stejnolehlé a v této stejnolehlosti se střed kružnice opsané
jsou stejnolehlé a v této stejnolehlosti se střed kružnice opsané  , bod
, bod 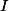 , se zobrazí na střed kružnice opsané
, se zobrazí na střed kružnice opsané  , bod
, bod 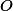 , a ortocentrum
, a ortocentrum  , bod
, bod  , se zobrazí na ortocentrum
, se zobrazí na ortocentrum  , bod
, bod 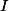 . Celkově dostaneme, že
. Celkově dostaneme, že  leží na jedné přímce.
leží na jedné přímce.
Zadání 4. úlohy:+ skrytý text
Najděte všechna reálná x taková, že \sqrt{5-x}=5-x^2
Štěpán Šimsa | org | 28. 6. 2015 00:12:19
Ahoj. Jen malé upřesnění k onomu řešení: + skrytý text
Pro využití AG nerovností potřebujeme, aby  byla kladná čísla. Ale snadno vidíme, že maximálně jedno z nich je záporné a pak nerovnost před přepsáním do těchto proměnných triviálně platí, protože levá strana je záporná a pravá kladná.
byla kladná čísla. Ale snadno vidíme, že maximálně jedno z nich je záporné a pak nerovnost před přepsáním do těchto proměnných triviálně platí, protože levá strana je záporná a pravá kladná.
Josef Svoboda | 26. 6. 2015 19:09:03
Ahoj, nějak se to řešení 2. úlohy rozsypalo. Tady je ještě jednou:
+ skrytý text
+ skrytý text
Podmínky  se ekvivaletně zbavíme substitucí
se ekvivaletně zbavíme substitucí  ,
,  ,
,  . Nerovnost přejde do tvaru
. Nerovnost přejde do tvaru  . Pro důkaz této nerovnosti vyjděme z nerovnosti
. Pro důkaz této nerovnosti vyjděme z nerovnosti  , která je součinem tří jednoduchých AG nerovností. Naši nerovnost z ní dostaneme dosazením
, která je součinem tří jednoduchých AG nerovností. Naši nerovnost z ní dostaneme dosazením  ,
,  a
a  .
.
Josef Svoboda | 26. 6. 2015 18:24:40
Ahoj.
Pěkné řešení Danile! Protože Tvou úlohu už dva týdny nevyřešil, předkládáme naše řešení.
Řešení úlohy č.2:+ skrytý text
Zadání úlohy č.3:+ skrytý text
Pepa a Štěpán
Pěkné řešení Danile! Protože Tvou úlohu už dva týdny nevyřešil, předkládáme naše řešení.
Řešení úlohy č.2:+ skrytý text
Podmínky  se ekvivaletně zbavíme substitucí
se ekvivaletně zbavíme substitucí  ,
,  ,
,  . Nerovnost přejde do tvaru
. Nerovnost přejde do tvaru  . Pro důkaz této nerovnosti vyjděme z nerovnosti
. Pro důkaz této nerovnosti vyjděme z nerovnosti  , která je součinem tří jednoduchých AG nerovností. Naši nerovnost z ní dostaneme dosazením
, která je součinem tří jednoduchých AG nerovností. Naši nerovnost z ní dostaneme dosazením  ,
,  ,
,  .
.
. Zadání úlohy č.3:+ skrytý text
V trojúhelníku 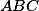 označme
označme  body dotyku kružnice vepsané se stranami trojúhelníka
body dotyku kružnice vepsané se stranami trojúhelníka 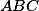 . Dále označme
. Dále označme  postupně střed kružnice opsané trojúhelníka
postupně střed kružnice opsané trojúhelníka 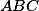 , střed kružnice vepsané trojúhelníka
, střed kružnice vepsané trojúhelníka 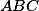 a průsečík výšek trojúhelníka
a průsečík výšek trojúhelníka  . Dokaž, že
. Dokaž, že  a
a  leží v jedné přímce.
leží v jedné přímce.
Pepa a Štěpán
Danil | 11. 6. 2015 12:22:01
Zdravím všechny, jelikož jsem si konečně vzpomněl na něco zajímavého, co bych tady mohl zadat, tak bych chtěl navázat v maratonu, zvěřejňuji řešení první úlohy a zadání té svojí, rovněž spíše rozjezdové.
Jelikož už je dokonce po termínu odevzdání 2. série iKSka, tak se teď můžou maratonu trochu víc věnovat i jeho řešitelé, takže počítám s tím, že má úloha moc dlouho nevydrží :)
Řešení úlohy č.1:
+ skrytý text
Zadání úlohy č.2:
+ skrytý text
Jelikož už je dokonce po termínu odevzdání 2. série iKSka, tak se teď můžou maratonu trochu víc věnovat i jeho řešitelé, takže počítám s tím, že má úloha moc dlouho nevydrží :)
Řešení úlohy č.1:
+ skrytý text
Sčítance na levé straně zřejmě také nabývají hodnot  a
a  , je jich dohromady n. Bude rovna nule právě tehdy, je-li polovina z nich kladná a polovina záporná, z čehož lze vyvodit, že je n sudé. Nyní pro spor předpokládejme, že je n ve tvaru
, je jich dohromady n. Bude rovna nule právě tehdy, je-li polovina z nich kladná a polovina záporná, z čehož lze vyvodit, že je n sudé. Nyní pro spor předpokládejme, že je n ve tvaru  pro nějaké celé k, tudíž je
pro nějaké celé k, tudíž je  ze sčítanců na levé straně rovno 1 a
ze sčítanců na levé straně rovno 1 a  rovno -1. To znamená, že je jejich součin
rovno -1. To znamená, že je jejich součin roven -1, protože v něm je lichý počet -1. Lze však snadno nahlédnout, že se v daném součinu vyskytne každé číslo
roven -1, protože v něm je lichý počet -1. Lze však snadno nahlédnout, že se v daném součinu vyskytne každé číslo  čtyřikrát a je tedy roven součinu jejich čtvrtých mocnin. No a když je součin čtvrtých mocnin reálných čísel záporný, tak je něco špatně a máme požadovaný spor, proto musí být n dělitelné 4.
čtyřikrát a je tedy roven součinu jejich čtvrtých mocnin. No a když je součin čtvrtých mocnin reálných čísel záporný, tak je něco špatně a máme požadovaný spor, proto musí být n dělitelné 4.
Zadání úlohy č.2:
+ skrytý text
Buď a, b, c kladná réalná čísla se součinem 1. Dokažte, že je hodnota součinu  nejvýše 1.
nejvýše 1.
Štěpán Šimsa | org | 2. 6. 2015 01:22:30
Ahoj,
určitě je Ti líto, že už letos skončily všechny PraSečí série (a první dvě série na příští rok už máš dávno vyřešené) a rád by sis vyřešil nějakou matematickou úložku. Proto jsme se rozhodli obnovit matematický maraton!
Pravidla jsou jednoduchá: přečteš si aktuální úlohu, tu vyřešíš a rovnou zadáš novou. Máš tak možnost nejen řešit zajímavé úlohy, ale také se podělit o příklady, které Ti připadají zajímavé. Nudící se orgové se taky možná občas zapojí :).
Tak tedy na rozjezd první úloha:
Každé z čísel je
je  nebo
nebo  a platí
a platí  . Dokažte, že
. Dokažte, že  je dělitelné čtyřmi.
je dělitelné čtyřmi.
určitě je Ti líto, že už letos skončily všechny PraSečí série (a první dvě série na příští rok už máš dávno vyřešené) a rád by sis vyřešil nějakou matematickou úložku. Proto jsme se rozhodli obnovit matematický maraton!
Pravidla jsou jednoduchá: přečteš si aktuální úlohu, tu vyřešíš a rovnou zadáš novou. Máš tak možnost nejen řešit zajímavé úlohy, ale také se podělit o příklady, které Ti připadají zajímavé. Nudící se orgové se taky možná občas zapojí :).
Tak tedy na rozjezd první úloha:
Každé z čísel
Martin Hora | org | 8. 5. 2015 09:32:35
Ahoj,
máme tady nápovědy k poslední jarní sérii.
úloha 1
a)+ skrytý text
b)+ skrytý text
úloha 2
a)+ skrytý text
b)+ skrytý text
úloha 3
a)+ skrytý text
b)+ skrytý text
úloha 4
a)+ skrytý text
b)+ skrytý text
úloha 5
a)+ skrytý text
b)+ skrytý text
úloha 6
a)+ skrytý text
b)+ skrytý text
úloha 7
a)+ skrytý text
b)+ skrytý text
máme tady nápovědy k poslední jarní sérii.
úloha 1
a)+ skrytý text
Nejprve si rozmyslete, že musí existovat přímka, která obsahuje body právě dvou barev, nebo přímka, která obsahuje vrcholy právě tří barev. Oba tyto případy rozeberte zvlášť. + skrytý text
Na trojbarevné přímce uvažujte body A, B, C po dvou různých barev takové, že B leží na úsečce AC. Pak se podívejte na průsečík kružnice nad AC a kolmice na AC procházející B.
b)+ skrytý text
Rozdělte strany trojúhelníku na třetiny. Tím dostanete celkem 9 bodů (i s původními vrcholy trojúhelníku.). Nalezněte pravoúhlé trojúhelníky, který tyto vrcholy tvoří a následně zkuste sporem dokázat, že alespoň jeden z těchto pravoúhlých trojúhelníků má všechny vrcholy obarvené stejnou barvou.
úloha 2
a)+ skrytý text
Uvažujme společnou tečnu kružnic k a l procházející bodem Q. Tuto tečnu zobrazíme dvakrát ve stejnolehlosti. Poprvé v záporné stejnolehlosti, která převádí k na m, a podruhé v záporné stejnolehlosti, která převádí l na m. Co tím dostaneme?
b)+ skrytý text
Předpokládejme, že jsou body A, B, C, D na kružnici v tomto pořadí. Jiné případy se pak vyřeší obdobně. Označme H průsečík BC a AD a O střed AB. Dále úhlete jako diví a využívejte Thaletovy kružnice. Postupně zkuste dokázat, že DOCE je tětivový, E je střed kružnice opsané DCH, DHCF je tětivový. Poté by už měla být hračka úlohu dorazit.
úloha 3
a)+ skrytý text
Ukažte, že Tondovo číslo je kongruentní součtu čísel 11111 + 11112 + ... + 99999 modulo 11111.+ skrytý text
Tondovo čislo si napište jako sumu jednotlivých pěticiferných čísel krát vhodná mocnina desítky a využijte toho, že 100000 je kongruentní 1 mod 11111.
b)+ skrytý text
Je-li n liché, pak n^8+1 je sudé. Jaké pak bude nejmenší prvočíslo, které toto číslo dělí?
Je-li n sudé, tak n^8+1 je liché. V tomto případě dokažte, že hledané prvočíslo má tvar 8k+1 pro nějaké přirozené k.+ skrytý text
Je-li n sudé, tak n^8+1 je liché. V tomto případě dokažte, že hledané prvočíslo má tvar 8k+1 pro nějaké přirozené k.+ skrytý text
Dokažte sporem s využitím Malé Fermatovy věty, že prvočíslo nemůže být tvaru 4k+3 ani tvaru 8k+5.
úloha 4
a)+ skrytý text
Využijte rozkladu a^3 + b^3 = (a+b)(a^2 -ab + b^2). Dále využívejte rovnosti sin^2 x + cos^2 x = 1 a 2sin(x)cos(x) = sin 2x. V určité fázi budete muset nejspíše rovnici umocnit nadruhou.
b)+ skrytý text
Rovnici vynásobte sin 1° a následně využijte vzorce pro součin sínů. 2 * sin x * sin y = cos(x-y) - cos(x+y).
úloha 5
a)+ skrytý text
Rozebereme zvlášť dva případy.
1) U stolu sedí zástupci pouze 2 politických stran.
2) U stolu sedí zástupci alespoň 3 politických stran, pak musí existovat dvojice sousedních židlí, na kterých sedí 4 politici, kteří jsou členy celkem aspoň 3 politických stran.
1) U stolu sedí zástupci pouze 2 politických stran.
2) U stolu sedí zástupci alespoň 3 politických stran, pak musí existovat dvojice sousedních židlí, na kterých sedí 4 politici, kteří jsou členy celkem aspoň 3 politických stran.
b)+ skrytý text
Pro n=1 vyhraje první strana. Ve všech ostatních situacích vyhraje druhá strana.
Je-li n sudé, tak je lehké najít vyhrávající strategii druhé strany. + skrytý text
Je-li n liché, tak nám přibude prostřední liché políčko. Zkuste strategii z předchozího případu upravit tak, aby uměla správně reagovat i na soupeřův tah na prostřední pole.
Je-li n sudé, tak je lehké najít vyhrávající strategii druhé strany. + skrytý text
Jen symetricky kopíruje první stranu.
Je-li n liché, tak nám přibude prostřední liché políčko. Zkuste strategii z předchozího případu upravit tak, aby uměla správně reagovat i na soupeřův tah na prostřední pole.
úloha 6
a)+ skrytý text
Rozeberte případ, kdy jedno z čísel a, b, c je nulové. + skrytý text
Dále se podívejte co se stane, pokud jedno z čísel a, b, c má opačné znaménko než zbylé dvě. + skrytý text
Dokažte, že pak má rovnice kořeny pomocí Vietových vztahů.
Dále se podívejte co se stane, pokud jedno z čísel a, b, c má opačné znaménko než zbylé dvě. + skrytý text
Dokažte, že pak je diskriminant kladný.
b)+ skrytý text
Napište si všechny 3 rovnice Vietových vztahů platící pro tento polynom a vhodně je sečtěte. Vzniklou rovnici upravte a diskutujte, co by se stalo, kdyby žádný z kořenů neležel ve stanoveném intervalu.
úloha 7
a)+ skrytý text
Nalezněte hvězdy, jejichž stav může Zeus změnit a současně ponechat stav ostatních hvězd. Zbylé hvězdy pak splňují, že na každé linii jich leží sudý počet. Co to znamená?
b)+ skrytý text
Mřížové body můžeme rozdělit do dvou skupin. Na ty, jejichž součet souřadnic je sudý, a na ty, jejichž součet souřadnic je lichý. Ukažte, že lichý bod se rotací přesune opět na lichý bod a sudý opět na sudý.
Máme-li sudý a lichý bod, pak je tedy nemůžeme prohodit. Co dělat pokud máme dva sudé body? A co když máme dva liché?
Máme-li sudý a lichý bod, pak je tedy nemůžeme prohodit. Co dělat pokud máme dva sudé body? A co když máme dva liché?
Martin Hora | org | 18. 4. 2015 15:03:40
Ahoj,
nápovědy k třetí jarní sérii a ke třetímu dílu seriálu jsou tady.
Jarní série:
úloha 1+ skrytý text
úloha 2+ skrytý text
úloha 3+ skrytý text
úloha 4+ skrytý text
úloha 5+ skrytý text
úloha 6+ skrytý text
úloha 7+ skrytý text
úloha 8+ skrytý text
Seríál:
úloha 1+ skrytý text
úloha 2+ skrytý text
úloha 3+ skrytý text
nápovědy k třetí jarní sérii a ke třetímu dílu seriálu jsou tady.
Jarní série:
úloha 1+ skrytý text
Nejdříve zkuste nakreslit 2 souhvězdí splňující zadání a poté zkuste přidat i souhvězdí třetí.
úloha 2+ skrytý text
Ano, mohlo se mu to podařit. Každá Davidova hvězda musí sousedit hranou s dalšími šesti hvězdami.
úloha 3+ skrytý text
Co když bude většina hvězd na jedné přímce?+ skrytý text
Na jedné přímce bude ležet 98 hvězd.
úloha 4+ skrytý text
Uvažujme tři přímky procházející Zemí takové, že každé dvě svírají spolu úhel 60°. Tyto přímky rozdělí oblohu na šest částí. Dokažte, že všechny hvězdy v každé z těchto částí mohou být poryty jednou kružnicí ze zadání.
úloha 5+ skrytý text
Libovolně zvolíme astronoma A. Pokud každý další astronom hlasoval alespoň pro jednu stejnou hvězdu jako A, tak je jednoduché zadání splnit. Předpokládejme tedy, že existuje astronom B, který nehlasoval pro žádnou z hvězd, pro kterou hlasoval A.
Může existovat astronom C, který nehlasoval pro žádnou hvězdu, pro kterou hlasoval A, a ani pro žádnou hvězdu. pro kterou hlasoval B?
Zvolíme-li 20 hvězd, ty, pro které hlasoval A a B, tak budou všichni astronomové spokojeni. Nyní zbývá dokázat, že z těchto 20 hvězd můžeme 10 vypustit.+ skrytý text
Může existovat astronom C, který nehlasoval pro žádnou hvězdu, pro kterou hlasoval A, a ani pro žádnou hvězdu. pro kterou hlasoval B?
Zvolíme-li 20 hvězd, ty, pro které hlasoval A a B, tak budou všichni astronomové spokojeni. Nyní zbývá dokázat, že z těchto 20 hvězd můžeme 10 vypustit.+ skrytý text
Můžeme vypustit jednu z následujících 4 množin: první pětice A + první pětice B, první pětice A + druhá pětice B, druhá pětice B + první pětice A, druhá pětice A + druhá pětice B.
Zkuste si toto tvrzení dokázat sporem.
Zkuste si toto tvrzení dokázat sporem.
úloha 6+ skrytý text
Nejdříve si rozmyslete, že žádné tři hvězdy nemohou ležet na přímce.
Dále dokážeme, že více než 4 hvězdy nemohou tvořit pravidelnou galaxii. Pro spor předpokládáme, že máme galaxii s alespoň 5 hvězdami. Vybereme si 4 hvězdy, které tvoří rovnoběžník s největším obsahem.
Kde je pátý bod (netvořící rovnoběžník)? Může být venku z rovnoběžníku? Může být uvnitř?
Dále dokážeme, že více než 4 hvězdy nemohou tvořit pravidelnou galaxii. Pro spor předpokládáme, že máme galaxii s alespoň 5 hvězdami. Vybereme si 4 hvězdy, které tvoří rovnoběžník s největším obsahem.
Kde je pátý bod (netvořící rovnoběžník)? Může být venku z rovnoběžníku? Může být uvnitř?
úloha 7+ skrytý text
Nejvíce může mít 12 hvězd. Zkuste najít rozestavení s 12 hvězdami, které splňuje zadání.+ skrytý text
Dál dokážeme, že 13 hvězd je již příliš mnoho. Rozmyslete si, že pokud máme čtveřici hvězd, které mají všechny stejnou svítivost nebo mají všechny po dvou různou svítivost, tak jejich jediným možným rozestavením je obdélník. Dále si rozmyslete, že nemůžeme mít pětici hvězd s touto vlastností.
Máme-li 13 hvězd, kolik mohou mít různých svítivostí? Rozmyslete si, že také musíme mít 2 čtveřice hvězd dříve popsané vlastnosti takové, že sdílí 3 hvězdy. Máme pak prostor, kam umístit zbylé hvězdy těchto čtveřic?
V tomto rozestavení budou 3 různé hodnoty svítivosti hvězd.
Dál dokážeme, že 13 hvězd je již příliš mnoho. Rozmyslete si, že pokud máme čtveřici hvězd, které mají všechny stejnou svítivost nebo mají všechny po dvou různou svítivost, tak jejich jediným možným rozestavením je obdélník. Dále si rozmyslete, že nemůžeme mít pětici hvězd s touto vlastností.
Máme-li 13 hvězd, kolik mohou mít různých svítivostí? Rozmyslete si, že také musíme mít 2 čtveřice hvězd dříve popsané vlastnosti takové, že sdílí 3 hvězdy. Máme pak prostor, kam umístit zbylé hvězdy těchto čtveřic?
úloha 8+ skrytý text
Hvězdy si rozdělíme do 4 skupin po 500. Dále ukážeme, že na jakýkoliv tah Jupitera může Mars zareagovat tak, aby neizoloval žádnou hvězdu.
Jak bude Mars hrát, zruší-li Jupiter most mezi hvězdami jedné skupiny? A jak bude hrát, zruší-li Jupiter most mezi 2 skupinami?
Jak bude Mars hrát, zruší-li Jupiter most mezi hvězdami jedné skupiny? A jak bude hrát, zruší-li Jupiter most mezi 2 skupinami?
Seríál:
úloha 1+ skrytý text
Vyhovuje například graf s 5 vrcholy, který vypadá tak, že čtyři vrcholy tvoří čtverec a pátý je uvnitř tohoto čtverce a je spojený se všemi ostatními vrcholy.
Rozmyslete si, že tento graf skutečně splňuje zadání.
Rozmyslete si, že tento graf skutečně splňuje zadání.
úloha 2+ skrytý text
Budeme předpokládat, že jeden směr úseček je rovnoběžný s osou x a druhý směr je rovnoběžný s osou y. Dále budeme předpokládat, že žádné dvě rovnoběžné úsečky neleží na stejné přímce. (Kdyžtak jednu úsečku trochu posuneme.)
Vodorovné úsečky očíslujeme zdola nahoru a svislé zleva doprava. Nyní si rozmyslete, že podmínka ze zadání za této situace musí nastat.
Dále dokážeme opačnou implikaci.
Vytvoříme si tabulku k x l. Políčko (i,j) v tabulce vybarvíme, pokud je vrchol i první partity spojen hranou s vrcholem j druhé partity. Pak v každém řádku a sloupci spojíme úsečkou nejkrajnější vybarvená políčka. Rozmyslete si, že se všechny úsečky protínají na vybavených políčkách.
Vodorovné úsečky očíslujeme zdola nahoru a svislé zleva doprava. Nyní si rozmyslete, že podmínka ze zadání za této situace musí nastat.
Dále dokážeme opačnou implikaci.
Vytvoříme si tabulku k x l. Políčko (i,j) v tabulce vybarvíme, pokud je vrchol i první partity spojen hranou s vrcholem j druhé partity. Pak v každém řádku a sloupci spojíme úsečkou nejkrajnější vybarvená políčka. Rozmyslete si, že se všechny úsečky protínají na vybavených políčkách.
úloha 3+ skrytý text
G obsahuje úplný podgraf na n vrcholech, potřebujeme tedy alespoň n barev. Dále dokážeme, že n barev stačí.
G je doplněk intervalového grafu. Kdy tedy mezi dvěma vrcholy G vede hrana?
Vrcholy si očíslujeme tak, aby odpovídaly seřazení intervalů zleva doprava. Následně začneme vrcholy grafu popořadě hladově obarvovat barvami 1 až n. Vždy použijeme barvu s nejnižším možným číslem. Co by znamenalo, že jsme při tomto algoritmu použili více než n barev?
G je doplněk intervalového grafu. Kdy tedy mezi dvěma vrcholy G vede hrana?
Vrcholy si očíslujeme tak, aby odpovídaly seřazení intervalů zleva doprava. Následně začneme vrcholy grafu popořadě hladově obarvovat barvami 1 až n. Vždy použijeme barvu s nejnižším možným číslem. Co by znamenalo, že jsme při tomto algoritmu použili více než n barev?
Miroslav Olšák | org | 25. 3. 2015 13:19:34
Věděli jste, že obecnější verze 6. úlohy celostátka byla před časem v PraSeti ;-) (osmička, s celkem elegantním řešením)
http://mks.mff.cuni.cz/common/show.php?title=...
http://mks.mff.cuni.cz/common/show.php?title=...
Štěpán Šimsa | org | 19. 3. 2015 01:44:11
A pokud jste trénink nestihli, tak máte čas až do neděle, abyste si vyzkoušeli alespoň "druhý den" tréninkového celostátka na TRiKSu!
Štěpán
Štěpán
Štěpán Šimsa | org | 16. 3. 2015 00:08:47
Ahoj,
za týden začíná celostátní kolo matematické olympiády a tak je načase začít s přípravami. Proto jsme si pro vás připravili speciální kolo soutěže TRiKS http://iksko.org/triks/current.php, kde si můžete vyzkoušet "celostátko na nečisto". Soutěže se můžete účastnit kdykoliv od teď až do středy a na tři úlohy máte 4,5 hodiny (stejně jako na skutečném celostátku). Soutěže se samozřejmě můžete zúčastnit i pokud jste se na celostátko nedostali nebo i pokud už jste na olympiádu příliš staří. Tak s chutí do toho!
Štěpán
za týden začíná celostátní kolo matematické olympiády a tak je načase začít s přípravami. Proto jsme si pro vás připravili speciální kolo soutěže TRiKS http://iksko.org/triks/current.php, kde si můžete vyzkoušet "celostátko na nečisto". Soutěže se můžete účastnit kdykoliv od teď až do středy a na tři úlohy máte 4,5 hodiny (stejně jako na skutečném celostátku). Soutěže se samozřejmě můžete zúčastnit i pokud jste se na celostátko nedostali nebo i pokud už jste na olympiádu příliš staří. Tak s chutí do toho!
Štěpán
Martin Hora | org | 12. 3. 2015 17:00:51
Ahoj,
máme tady nápovědy ke druhé jarní sérii
úloha 1+ skrytý text
úloha 2+ skrytý text
úloha 3+ skrytý text
úloha 4+ skrytý text
úloha 5+ skrytý text
úloha 6+ skrytý text
úloha 7+ skrytý text
úloha 8+ skrytý text
máme tady nápovědy ke druhé jarní sérii
úloha 1+ skrytý text
Zadání vyhovuje například polynom druhého stupně s absolutním členem rovným nule. Zkuste nějaký takový najít.
úloha 2+ skrytý text
Je-li x kořenem P(x) i Q(x), pak musí být i kořenem P(x)-Q(x). Zkuste se tedy zaměřit na kořeny polynomu P(x)-Q(x).
úloha 3+ skrytý text
Nejprve zvolme x = 0. Zjistíme, že P(0) = 0. Dále zkuste určit jakých funkčních hodnot polynom nabývá na přirozených číslech.+ skrytý text
Je to 0, důkaz lze provést matematickou indukcí. Pak již jen zbývá určit, co z toho plyne pro daný polynom.
úloha 4+ skrytý text
Takový polynom neexistuje. Důkaz se provede sporem. Předpokládejme, že takový polynom existuje a má nějaký racionální kořen p/q, kde p a q jsou nesoudělné. Zkusme tento kořen dosadit do polynomu a podívat se na vzniklou rovnici modulo dvěma.
úloha 5+ skrytý text
Ze zadaného polynomu P(x) vytkneme (x-2015). Dostaneme P(x) = (x-2015)Q(x), kde Q(x) je polynom stupně o jedna menší než P(x). Nahlédneme, že polynom Q(x) má opět celočíselné koeficienty.
Dále budeme postupovat sporem. Budeme předpokládat, že všechny koeficienty P(x) jsou větší než -2015. Co z toho plyne pro polynom Q(x)?
Dále budeme postupovat sporem. Budeme předpokládat, že všechny koeficienty P(x) jsou větší než -2015. Co z toho plyne pro polynom Q(x)?
úloha 6+ skrytý text
Uvažte polynomy třetího stupně P(t) a Q(t) takové, že P(t) má kořeny a, b, c a Q(t) má kořeny x, y, z. Jak tyto polynomy vypadají?
Rozmyslete si, jak vypadají grafy těchto polynomů uvážíte-li podmínky ze zadání. Do obou polynomů dosaďte maximum z čísel a, b, c. Z tohoto dosazení získáte nějakou zajímavou nerovnost.
Následně do obou polynomů dosaďte minimum z čísel a, b, c.
Rozmyslete si, jak vypadají grafy těchto polynomů uvážíte-li podmínky ze zadání. Do obou polynomů dosaďte maximum z čísel a, b, c. Z tohoto dosazení získáte nějakou zajímavou nerovnost.
Následně do obou polynomů dosaďte minimum z čísel a, b, c.
úloha 7+ skrytý text
Klíčem k této úloze jsou Vietovy vztahy. Zkuste pomocí nich dokázat, že všechny vyhovující polynomy mají stupeň nejvýše 3. Pak již jen stačí pro všechny z těchto polynomů ověřit, zdli splňují zadání.+ skrytý text
U Vietových vztahů zkuste využít, že druhá mocnina libovolného koeficientu polynomu je rovna +1.
úloha 8+ skrytý text
Označme d stupeň polynomu P(x). Uvažme polynom Q(x) stupně d takový, že Q(k) = f(k) pro k = 1, 2, ... , d + 1. Nyní je potřeba ověřit, že tento polynom Q(x) vyhovuje zadání
Polynom Q(x) má racionální koeficienty. Existuje tedy nějaké celé číslo M, že MQ(x) má celočíselné koeficienty. Pro všechna celá čísla n pak platí, že n-k dělí M(f(n)-f(k)) - M(Q(n)-Q(k)). Platí tedy že f(n) = Q(n), anebo je M(f(n)-Q(n)) větší než nejmenší společný násobek čísel n-1, n-2, ..., n-d-1. Výraz M(f(n)-Q(n)) však můžeme shora odhadnout nějakým násobkem polynomu P(x). Z těchto faktů lze sérií úvah odvodit, že Q(n) = f(n) pro dostatečně vysoká n.
Dokázat platnost tvrzení pro ostatní n by poté již nemělo být tak těžké.
Polynom Q(x) má racionální koeficienty. Existuje tedy nějaké celé číslo M, že MQ(x) má celočíselné koeficienty. Pro všechna celá čísla n pak platí, že n-k dělí M(f(n)-f(k)) - M(Q(n)-Q(k)). Platí tedy že f(n) = Q(n), anebo je M(f(n)-Q(n)) větší než nejmenší společný násobek čísel n-1, n-2, ..., n-d-1. Výraz M(f(n)-Q(n)) však můžeme shora odhadnout nějakým násobkem polynomu P(x). Z těchto faktů lze sérií úvah odvodit, že Q(n) = f(n) pro dostatečně vysoká n.
Dokázat platnost tvrzení pro ostatní n by poté již nemělo být tak těžké.
Petr | 24. 2. 2015 17:07:38
Koho zaujala osmá úloha první jarní série, tomu doporučuji
http://webspace.ship.edu/msrenault/ballotprob...
http://webspace.ship.edu/msrenault/ballotprob...
Martin Hora | org | 13. 2. 2015 13:16:57
Ahoj,
nápovědy k první jarní sérii a k druhému dílu seriálu jsou tady.
Jarní série:
úloha 1+ skrytý text
úloha 2+ skrytý text
úloha 3+ skrytý text
úloha 4+ skrytý text
úloha 5+ skrytý text
úloha 6+ skrytý text
úloha 7+ skrytý text
úloha 8+ skrytý text
Seríál:
úloha 1+ skrytý text
úloha 2+ skrytý text
úloha 3+ skrytý text
nápovědy k první jarní sérii a k druhému dílu seriálu jsou tady.
Jarní série:
úloha 1+ skrytý text
Nemusí. Stačí vytvořit vhodné rozložení preferencí voličů PraSestánu takové, že splňuje zadání a nadpoloviční většina voličů dává přednost Vepříkovi před Pašíkem.
úloha 2+ skrytý text
Zde je potřeba zkonstruovat síť ministerstev, která vyhovuje zadání. Dobrým základem je začít pouze se 4 ministerstvy a následně konstrukci pro 4 ministerstva vhodně rozšířit.
úloha 3+ skrytý text
Pokud m = 0, tak má politik (n-1)! možností jak vybrat pořadí měst v jakém je bude projíždět.
Uvažujme dvě města A a B (různé od hlavního města), které jsou spojena opravenou cestou. Politik musí během své kampaně navštívit obě dvě tato města. Pokud navštíví jako první z těchto dvou měst město A, tak z něj pak musí odjet přímo do města B po opravené silnici. Navštíví-li z nich dřívě město B, pak musí z něj po opravené silnici do města A. Z toho plyne, že města A a B musí na politikově turné následovat hned po sobě. Tyto 2 města tedy můžeme považovat za jedno, u kterého má politik 2 možnosti jak ho projet.
Zbývá ještě odlišit dva případy, pokud z hlavního města vede opravená silnice a pokud ne. Rozmyslete si v čem se tyto 2 případy liší a dopočtěte kolika způsoby může politik uskutečnit svou kampaň.
Uvažujme dvě města A a B (různé od hlavního města), které jsou spojena opravenou cestou. Politik musí během své kampaně navštívit obě dvě tato města. Pokud navštíví jako první z těchto dvou měst město A, tak z něj pak musí odjet přímo do města B po opravené silnici. Navštíví-li z nich dřívě město B, pak musí z něj po opravené silnici do města A. Z toho plyne, že města A a B musí na politikově turné následovat hned po sobě. Tyto 2 města tedy můžeme považovat za jedno, u kterého má politik 2 možnosti jak ho projet.
Zbývá ještě odlišit dva případy, pokud z hlavního města vede opravená silnice a pokud ne. Rozmyslete si v čem se tyto 2 případy liší a dopočtěte kolika způsoby může politik uskutečnit svou kampaň.
úloha 4+ skrytý text
Tuto úlohu vyřešíme sporem. Předpokládejme, že taková trojice politiků neexistuje. Pak se zaměřme na toho politika (označme ho x a jeho stranu A), jehož y přátel náleží do jedné strany (tu označme B), přičemž platí že y je maximální takové. (Tedy neexistuje žádný jiný politik, jehož y+1 přátel by bylo z jedné strany). Politik x má určitě nějakého přítele w ve třetí straně C. Kolik přátel má w ve stranách B a A? Co z toho plyne?
úloha 5+ skrytý text
Kdyby po propouštění zbylo více než 100 000 úředníků, tak by z Dirichletova principu museli existovat dva úředníci, kterří mají shodné poslední pětičíslí. Kódy těchto dvou úředníků by se tedy nelišily alespoň ve dvou cifrách.
Nyní zbývá dokázat, že stačí propustit jen 900 000 úředníků. To znamená, že existuje 100 000 úředníků, kde kód libovolných 2 se liší alespoň na dvou pozicích. + skrytý text
Nyní zbývá dokázat, že stačí propustit jen 900 000 úředníků. To znamená, že existuje 100 000 úředníků, kde kód libovolných 2 se liší alespoň na dvou pozicích. + skrytý text
Například si můžeme ponechat 100 000 úředníků tak, aby každý z těcto úředníků měl unikátní koncové pětičíslí a jako první cifru kódu doplnit zbytek po dělení deseti ciferného součtu posledního pětičíslí každého úředníka. Rozmyslete si, že tento postup splňuje zadání.
úloha 6+ skrytý text
Předpokládejme, že ve městě je alespoň jedna hlavní ulice. (Druhý případ je nezajímavý.) Pak je ve městě jistě ulice, která vede ven z města. (Opak by znamenal, že existuje neobdélníková čtvrť, která obkružuje celý zbytek města.) My po této silnici do města vejdeme a pokračujeme po ní rovně, dokud nenarazíme na její konec. Konec této ulice musí být nutně křižovatka tvaru T. (Rozmyslete si proč.) Na této křižovatce se rozhlédneme vpravo a vlevo. Nejvýše na jedné straně uvidíme okraj města. My se dále vydáme na stranu, kde okraj města nevidíme. (Jsou-li dvě, tak je jedno na kterou.) Opět dojdeme až na konec této ulice a celý proces opakujeme.
Ulic i křižovatek je v městě jen konečně mnoho, takže časem během naší procházky musíme přijít na místo, kde už jsme jedou byli. Co z toho plyne?
Ulic i křižovatek je v městě jen konečně mnoho, takže časem během naší procházky musíme přijít na místo, kde už jsme jedou byli. Co z toho plyne?
úloha 7+ skrytý text
Na tuto úlohu použijeme matematickou indukci. Pokud je na nádvoří poze jedna židle nebo tam není žádná židle, tak politiky určitě rozesadit umím. Předpokládejme, že umíme rozesadit politiky máme-li 0 až k židlí. Podívejme se nyní na situaci, máme-li k+1 židlí. Pak mohou nastat dvě situace.
1) Existuje řada/sloupec ve které je pouze jedna židle.
2) Neexistuje sloupec ani řada, ve které by byla právě 1 židle.
V obou těchto případech umíme odebrat nějakou neprázdnou množinu židlí. Z indukčního předpokladu umíme rozesadit politiky na zbylé židle. Následně opět vrátíme odebranou množinu židlí a ukážeme, že na ně vždy můžeme dosadit politiky, ta aby bylo zadání splněno.
Zkuste si rozmyslet jakou množinu židlí budeme odebírat v případě 1) a jakou v případě 2).
1) Existuje řada/sloupec ve které je pouze jedna židle.
2) Neexistuje sloupec ani řada, ve které by byla právě 1 židle.
V obou těchto případech umíme odebrat nějakou neprázdnou množinu židlí. Z indukčního předpokladu umíme rozesadit politiky na zbylé židle. Následně opět vrátíme odebranou množinu židlí a ukážeme, že na ně vždy můžeme dosadit politiky, ta aby bylo zadání splněno.
Zkuste si rozmyslet jakou množinu židlí budeme odebírat v případě 1) a jakou v případě 2).
úloha 8+ skrytý text
Uspořádejme hlasovací lístky do kruhu libovolným způsobem.
Nyní v kruhu každý hlas pro A nahraďme +1 a každý hlas pro B nahraďme -k. Začněme na nějakém místě v kruhu sčítat tato čísla po směru hodinových ručiček. Pokud všechny průběžné součty, které takto dostaneme jsou kladné, tak místo odkud jsme začali označme jako dobré. Jinak toto místo označme jako špatné.
Nyní začněme pozice v kruhu označovat jako špatné. Postupně budeme procházet všechny -k v kruhu. Každé -k označíme jako špatné a pro každé -k půjdeme proti směru hodinových ručiček a prvních k plus jedniček , na které narazíme a které nejsou ještě nijak označeny, označíme jako špatné. Rozmyslete si, že takto označíme všechny špatné pozici a všechny pozice, které zbydou jsou dobré.
Kolik v každém kruhu zbyde dobrých pozic?
Pro každou posloupnost sčítání hlasů existuje právě jeden kruh. (Pootočené kruhy jsou stejné). Je-li v jednom kruhu nějaká posloupnost sčítání hlasů obsažena vícekrát, (to znamená, že kruh je po nějakém pootočení totožný), pak jsou všechny posloupnosti, kterým odpovídá daný kruh, obsaženy stejněkrát.
Na základě těchto poznatků určete jaká je výsledná pravděpodobnost.
Nyní v kruhu každý hlas pro A nahraďme +1 a každý hlas pro B nahraďme -k. Začněme na nějakém místě v kruhu sčítat tato čísla po směru hodinových ručiček. Pokud všechny průběžné součty, které takto dostaneme jsou kladné, tak místo odkud jsme začali označme jako dobré. Jinak toto místo označme jako špatné.
Nyní začněme pozice v kruhu označovat jako špatné. Postupně budeme procházet všechny -k v kruhu. Každé -k označíme jako špatné a pro každé -k půjdeme proti směru hodinových ručiček a prvních k plus jedniček , na které narazíme a které nejsou ještě nijak označeny, označíme jako špatné. Rozmyslete si, že takto označíme všechny špatné pozici a všechny pozice, které zbydou jsou dobré.
Kolik v každém kruhu zbyde dobrých pozic?
Pro každou posloupnost sčítání hlasů existuje právě jeden kruh. (Pootočené kruhy jsou stejné). Je-li v jednom kruhu nějaká posloupnost sčítání hlasů obsažena vícekrát, (to znamená, že kruh je po nějakém pootočení totožný), pak jsou všechny posloupnosti, kterým odpovídá daný kruh, obsaženy stejněkrát.
Na základě těchto poznatků určete jaká je výsledná pravděpodobnost.
Seríál:
úloha 1+ skrytý text
Dokážte, že hranová barevnost grafu je d. Důkaz má 2 části.
1) barevnost je alespoň d. Tato část je jednoduchá.
2) d barev nám stačí.+ skrytý text
1) barevnost je alespoň d. Tato část je jednoduchá.
2) d barev nám stačí.+ skrytý text
Na druhou část použijte matematickou indukci podle d. Při indukčním kroku použijte vhodně Hallovu větu.
úloha 2+ skrytý text
Duální graf G* ze zadání je rovinný. Z věty o 4-obarvitelnosti rovinného grafu jsme tedy dostaneme jednu implikaci.
Označme barvy G* a, b, c, d a barvy hran G x, y, z. Hrany G, které oddělují stěny G(vrcholy G*) s barvami (a,b) a (c,d) obarvíme barvou x, oddělující (a,c) a (b,d) barvou y a oddělující (a,d) a (b,c) barvou z. Dokažte, že toto vybarvení odpovídá zadání.
Označme barvy G* a, b, c, d a barvy hran G x, y, z. Hrany G, které oddělují stěny G(vrcholy G*) s barvami (a,b) a (c,d) obarvíme barvou x, oddělující (a,c) a (b,d) barvou y a oddělující (a,d) a (b,c) barvou z. Dokažte, že toto vybarvení odpovídá zadání.
úloha 3+ skrytý text
Prozradím, že se výsledném výrazu vyskytuje nějaké Fibonacciho číslo. Zkuste vymyslet vhodný výraz pro malá n. Důkaz se pak provede matematickou indukcí.
Správný výsledek:+ skrytý text
Správný výsledek:+ skrytý text
F(n+3) - 1
Miroslav Olšák | org | 27. 1. 2015 00:13:12
Po Slovenském vítězství ve Velkých cenách k jejich velkolepým úlohám příchází nápovědy. Dokážete je vyřešit alespoň s nimi?
úloha A
+ skrytý text
úloha C
První krok
+ skrytý text
+ skrytý text
úloha G
Hledaný bod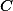 se dá popsat třeba takto (elementárně)
se dá popsat třeba takto (elementárně)
+ skrytý text
+ skrytý text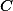 je společným stejnoúhlým kamarádem bodu
je společným stejnoúhlým kamarádem bodu 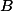 ve všech trojúhelnících
ve všech trojúhelnících  .Oba dva popisy vedou k řešení.
.Oba dva popisy vedou k řešení.
úloha N
Drobná nápověda
+ skrytý text
+ skrytý text
úloha A
+ skrytý text
dokažte 
+ skrytý text
+ skrytý text
dokažte  a
a 
+ skrytý text
+ skrytý text
dokažte 
+ skrytý text
+ skrytý text
dokažte, že  je rostoucí
je rostoucí
+ skrytý text
+ skrytý text
Z Cauchyovy vlastnosti a monotonie odvoďte řešení.
úloha C
První krok
+ skrytý text
Každé odpočívání nějakého hráče trvá  nebo
nebo  kol.
kol.
Nápověda+ skrytý text
Uvažte hráče 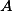 ,
,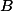 , kteří spolu hráli v prvním kole, BÚNO
, kteří spolu hráli v prvním kole, BÚNO 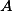 pak odpočíval
pak odpočíval  kol, zatímco
kol, zatímco 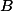 odpočíval
odpočíval  kol. Pro spor předpokládejte, že hráč
kol. Pro spor předpokládejte, že hráč 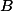 někdy (poprvé) odpočíval jen
někdy (poprvé) odpočíval jen  kol. Pak označte
kol. Pak označte 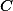 hráče, se kterým
hráče, se kterým 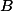 hrál po této pauze. Spor naleznete už na hráčích
hrál po této pauze. Spor naleznete už na hráčích 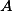 ,
, 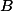 ,
, 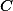 .
.
úloha G
Hledaný bod
+ skrytý text
Označte  ,
,  extrémní polohy bodů
extrémní polohy bodů 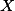 ,
, 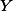 (když ten druhý je v nekonečnu). Doplňte na rovnoběžník
(když ten druhý je v nekonečnu). Doplňte na rovnoběžník  .
.
Nebo takto (pořádně)+ skrytý text
úloha N
Drobná nápověda
+ skrytý text
Uměli byste úlohy vyřešit, kdyby místo 11 bylo to prvočíslo 2? To je ještě docela lehké. A jak to teď to zobecnit pro prvočíslo 3...
Klíčový trik+ skrytý text
Řešte úlohu, kde místo počítání nulových bodů sčítáte (mod 11) všech  hodnot polynomu. Jaká musí být v takovém případě podmínka na stupeň polynomu, aby součet nutně vyšel nula?
hodnot polynomu. Jaká musí být v takovém případě podmínka na stupeň polynomu, aby součet nutně vyšel nula?
Vejtek | 19. 1. 2015 10:28:00
BakyX: Docela by mě zajímalo, jak to "derivuješ". Než jsem si ty multiplikátory napsal (musí se dvakrát, na té 2D ploše a na průniku s rovinou a=3), tak jsem si všiml těch "skorosymetrických" polynomů a udělal ten vzorový odhad. Přiznávám, že do dvou sekund jsem to ale neměl [o:





