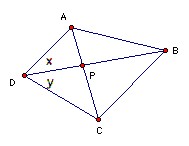

A convex polygon has all its sides and diagonals with rational length. It is dissected into smaller polygons by drawing all its diagonals. Show that the small polygons have all sides rational.
Solution
It is not hard to see that it is sufficient to prove the result for convex quadrilaterals. For in the case of an n-gon any side of a small polygon is either a side of the n-gon (in which case there is nothing to prove) or a segment of a diagonal. Suppose the diagonal is AiAj. Suppose the points of intersection along this diagonal are (in order) P0 = Ai, P1, P2, ... , Pm = Aj. Suppose Pk is the intersection of AiAj with ArAs. Then using the quadrilateral AiArAjAs we deduce that P0Pk (= AiPk) is rational. Hence PhPk = P0Pk - P0Ph is rational. So all the segments of the diagonal are rational.

It is immediate from the cosine rule that the angles in a triangle with rational sides have rational cosines. So cos x, cos y and cos(x+y) are rational (using triangles ABD, BCD, ADC). Using the formula for cos(x+y) it follows that sin x sin y is rational. Now sin2y = 1 - cos2y is rational, so sin x/sin y is rational.
Now area APD = (AD·PD sin x)/2 and area CPD = CD·PD sin y)/2, so AP/PC = area APD/area CPD = (sin x/sin y)(AD/CD) = rational. But AP + PC is rational, so AP is rational. Similarly for the other segments.
![]()
© John Scholes
jscholes@kalva.demon.co.uk
6 Aug 2003
Last corrected/updated 6 Aug 03