IMO shortlist 1997/23 solution

38th IMO 1997 shortlist

Problem 23

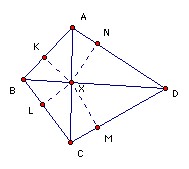
ABCD is a convex quadrilateral and X is the point where its diagonals meet. XA sin A + XC sin C = XB sin B + XD sin D. Show that ABCD must be cyclic.

Solution

Take perpendiculars from X to AB, BC, CD, DA with feet K, L, M, N respectively. Then the midpoint of AX is the center of the circle through A,K,X,N. Also KN subtends an angle 2∠A at the center, so KN = 2 x radius x sin(2A/2) = XA sin A. Thus the condition in the question gives KN + LM = MN + KL (**). But we also have KN = XK cos XKN + XN cos XNK = XK cos XAN + XN cos XAK (*)

Let us write ∠XAD = α₁, ∠XAB = α₂, ∠XBA = β₁, ∠XBC = β₂, ∠XCB = γ₁, ∠XCD = γ₂, ∠XDC = δ₁, ∠XDA = δ₂. Then (*) becomes KN = XK cos α₁ + XN cos α₂. Similarly, KL = XL cos β₁ + XK cos β₂, LM = XM cos γ₁ + XL cos γ₂, MN = XN cos δ₁ + XM cos δ₂. So (**) becomes, XK(cos α₁ - cos β₂) + XL(cos γ₂ - cos β₁) + XM(cos γ₁ - cos δ₂) + XN(cos α₂ - cos δ₁) = 0 (***).

There is no loss of generality in assuming that α₁ ≤ β₂. That is equivalent to A lying outside the circumcircle of BCD and hence to α₂ ≤ δ₁. But α₁ + δ₂ = β₂ + γ₁, so γ₁ ≤ δ₂. Similarly, α₂ + β₁ = γ₂ + δ₁, so γ₂ ≤ β₁. The cosine function is decreasing over the range 0^o to 180^o, so it follows that all the parentheses in (***) are non-negative. Hence they must all be zero, and all the pairs of angles equal. It follows that ABCD is cyclic.

38th IMO shortlist 1997