33rd IMO 1992 shortlist

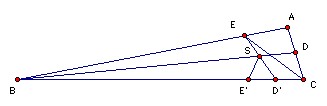
BD and CE are angle bisectors of the triangle ABC. ∠BDE = 24^o and ∠CED = 18^o. Find angles A, B, C.

Solution

∠SBC + ∠SCB = 180^o - ∠BSC = ∠SED + ∠SDE = 42^o. Hence ∠B + ∠C = 84^o, so ∠A = 96^o.

Take D' on BC such that CD' = CD, and E' on BC such that BE' = BE. Let ED' meet BD at S. ∠ESB = ∠SED + ∠SDE = 2·18^o + 24^o = 60^o. Hence ∠E'SB = 60^o. Hence ∠D'SE' = 60^o. So E'S is the external bisector of ∠D'SD.

Now EC is perpendicular to DD', so ∠EDD' = 90^o - ∠CED = 72^o. ∠EDE' = 2·24^o, so ∠E'DD' = 72^o - 48^o = 24^o. But ∠E'DS = ∠EDS = 24^o, so E'D is the bisector of ∠SDD'. Hence E' must also lie on the external bisector of ∠DD'S. In other words, ∠E'D'S = ∠CD'D. But ∠ED'D = 180^o - ∠D'ED - ∠D'DE = 180^o - 2·18^o - 72^o = 72^o. Hence ∠CD'D = (180^o - 72^o)/2 = 54^o. Hence ∠C = 180^o - 2·54^o = 72^o. Hence ∠B = 12^o.

33rd IMO shortlist 1992

© John Scholes
jscholes@kalva.demon.co.uk
25 Nov 2003
Last updated/corrected 25 Nov 2003