|
|
1. Given real A, find all solutions (x1, x2, ... , xn) to the n equations (i = 1, 2, ... , n):
xi |xi|- (xi - A) |(xi - A)| = xi+1 |xi+1|, where we take xn+1 to mean x1. (France 1)
|
|
|
2. Prove that there are infinitely many triples of positive integers (m, n, p) satisfying 4mn - m - n = p2 - 1, but none satisfying 4mn - m - n = p2. (Canada 2)
|

|
|
3. Find all positive integers n such that n = d62 + d72 - 1, where 1 = d1 < d2 < ... < dk = n are all the positive divisors of n. (USSR 3)
|
|
|
6. c is a positive integer. The sequence f1, f2, f3, ... is defined by f1 = 1, f2 = c, fn+1 = 2 fn - fn-1 + 2. Show that for each k there is an r such that fk fk+1 = fr. (Canada 3)
|

|
|
7. Can we number the squares of an 8 x 8 board with the numbers 1, 2, ... , 64 so that any four squares with any of the following shapes
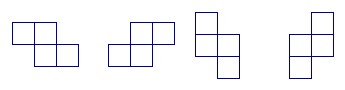
have sum = 0 mod 4? Can we do it for the following shapes?
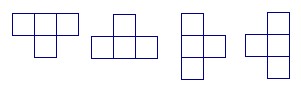 (German Federal Republic 5) (German Federal Republic 5)
|
|
9. Let a, b, c be positive reals such that √a + √b + √c = √3/2. Show that the equations:
√(y - a) + √(z - a) = 1
√(z - b) + √(x - b) = 1
√(x - c) + √(y - c) = 1
have exactly one solution in reals x, y, z. (Poland 2)
|
|
|
10. Prove that the product of five consecutive positive integers cannot be the square of an integer. (Great Britain 1)
|

|
|
11. a1, a2, ... , a2n are distinct integers. Find all integers x which satisfy (x - a1)(x - a2) ... (x - a2n) = (-1)n(n!)2. (Canada 1)
|
|
|
13. A tetrahedron is inscribed in a straight circular cylinder of volume 1. Show that its volume cannot exceed 2/(3π). (Bulgaria 5)
|
|
|
15. The angles of the triangle ABC are all < 120o. Equilateral triangles are constructed on the outside of each side as shown. Show that the three lines AD, BE, CF are concurrent. Suppose they meet at S. Show that SD + SE + SF = 2(SA + SB + SC).
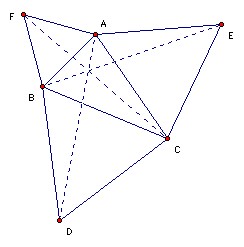 (Luxembourg 2) (Luxembourg 2)
|
|
|
17. If (x1, x2, ... , xn) is a permutation of (1, 2, ... , n) we call the pair (xi, xj) discordant if i < j and xi > xj. Let d(n, k) be the number of permutations of (1, 2, ... , n) with just k discordant pairs. Find d(n, 2) and d(n, 3). (German Federal Republic 3)
|
|
|
18. ABC is a triangle. A circles with the radii shown are drawn inside the triangle each touching two sides and the incircle. Find the radius of the incircle.
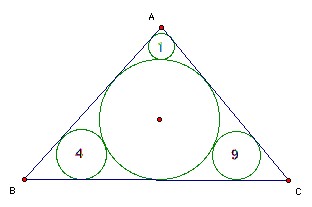 (USA 5)
(USA 5)
|
|
19. The harmonic table is a triangular array:
1
1/2 1/2
1/3 1/6 1/3
1/4 1/12 1/12 1/4
...
where an,1 = 1/n and an,k+1 = an-1,k - an,k. Find the harmonic mean of the 1985th row. (Canada 5)
|
|
|
20. Find all pairs of positive reals (a, b) with a not 1 such that logab < loga+1(b+1). (USA 2)
|
|
|
Note: This list does not incude the problems used in the Olympiad (4, 5, 8, 12, 14, 16 on the shortlist, which were 5, 1, 3, 2, 4, 6 in the Olympiad).
|
|

 (German Federal Republic 5)
(German Federal Republic 5)
 (Luxembourg 2)
(Luxembourg 2)
 (USA 5)
(USA 5)
