IMO 1999/B2 solution

IMO 1999

Problem B2

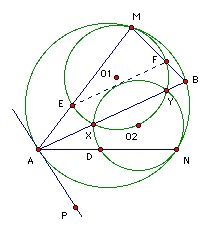
The circles C₁ and C₂ lie inside the circle C, and are tangent to it at M and N, respectively. C₁ passes through the center of C₂. The common chord of C₁ and C₂, when extended, meets C at A and B. The lines MA and MB meet C₁ again at E and F. Prove that the line EF is tangent to C₂.

Solution

Solution by Jean-Pierre Ehrmann

Let O, O₁, O₂ and r, r₁, r₂ be the centers and radii of C, C₁, C₂ respectively. Let EF meet the line O₁O₂ at W, and let O₂W = x. We need to prove that x = r₂.

Take rectangular coordinates with origin O₂, x-axis O₂O₁, and let O have coordinates (a, b). Notice that O and M do not, in general, lie on O₁O₂. Let AB meet the line O₁O₂ at V.

We observe first that O₂V = r₂²/(2 r₁). [For example, let X be a point of intersection of C₁ and C₂ and let Y be the midpoint of O₂X. Then O₁YO₂ and XVO₂ are similar. Hence, O₂V/O₂X = O₂Y/O₂O₁.]

An expansion (or, to be technical, a homothecy) center M, factor r/r₁ takes O₁ to O and EF to AB. Hence EF is perpendicular to O₁O₂. Also the distance of O₁ from EF is r₁/r times the distance of O from AB, so (r₁ - x) = r₁/r (a - r₂²/(2 r₁) ) (*).

We now need to find a. We can get two equations for a and b by looking at the distances of O from O₁ and O₂. We have:
(r - r₁)² = (r₁ - a)² + b², and
(r - r₂)² = a² + b².

Subtracting to eliminate b, we get a = r₂²/(2 r₁) + r - r r₂/r₁. Substituting back in (*), we get x = r₂, as required.

Alternative solution by Marcin Kuczma, communicated Arne Smeets

Let C₁ and C₂ meet at X and Y, and let AN meet C₂ again at D. Then AE·AM = AX·AY = AD·AN, so triangles AED and ANM are similar. Hence ∠ADE = ∠AMN.

Take the tangent AP as shown. Then ∠PAN = ∠AMN = ∠ADE, so AP and DE are parallel. The homothecy center M mapping C to C₁ takes the line AP to the line ED, so ED is tangent to C₁ at E. A similar argument show that it is tangent to C₂ at D. The homothecy takes AB to EF, so EF is perpendicular to O₁O₂ (the line of centers). Hence O₂EF is isosceles. So angle O₂EF = angle O₂FE = angle DEO₂ (DE tangent). In other words, O₂E bisects angle DEF. But ED is tangent to C₂, so EF is also.

40th IMO 1999