IMO 2002/B3 solution

IMO 2002

Problem B3

2 circles of radius 1 are drawn in the plane so that no line meets more than two of the circles. Their centers are O₁, O₂, ... , O_n. Show that ∑_i<j 1/O_iO_j ≤ (n-1)π/4.

Solution

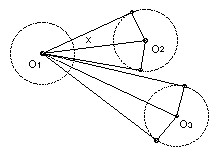
Denote the circle center O_i by C_i. The tangents from O₁ to C_i contain an angle 2x where sin x = 1/O₁O_i. So 2x > 2/O₁O_i. These double sectors cannot overlap, so ∑ 2/O₁O_i < π. Adding the equations derived from O₂, O₃, ... we get 4 ∑ O_iO_j < nπ, so ∑ O_iO_j < nπ/4, which is not quite good enough.

There are two key observations. The first is that it is better to consider the angle O_iO₁O_j than the angle between the tangents to a single circle. It is not hard to show that this angle must exceed both 2/O₁O_i and 2/O₁O_j. For consider the two common tangents to C₁ and C_i which intersect at the midpoint of O₁O_i. The angle between the center line and one of the tangents is at least 2/O₁O_i. No part of the circle C_j can cross this line, so its center O_j cannot cross the line parallel to the tangent through O₁. In other word, angle O_iO₁O_j is at least 2/O₁O_i. A similar argument establishes it is at least 2/O₁O_j.

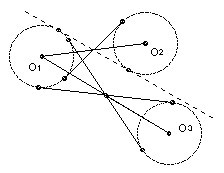
Now consider the convex hull of the n points O_i. m ≤ n of these points form the convex hull and the angles in the convex m-gon sum to (m-2)π. That is the second key observation. That gains us not one but two amounts π/4. However, we lose one back. Suppose O₁ is a vertex of the convex hull and that its angle is θ₁. Suppose for convenience that the rays O₁O₂, O₁O₃, ... , O₁O_n occur in that order with O₂ and O_n adjacent vertices to O₁ in the convex hull. We have that the n-2 angles between adjacent rays sum to θ₁. So we have ∑ 2/O₁O_i < θ₁, where the sum is taken over only n-2 of the i, not all n-1. But we can choose which i to drop, because of our freedom to choose either distance for each angle. So we drop the longest distance O₁O_i. [If O₁O_k is the longest, then we work outwards from that ray. Angle O_k-1O₁O_k > 2/O₁O_k-1, and angle O_kO₁O_k+1 > 2/O₁O_k+1 and so on.]

We now sum over all the vertices in the convex hull. For any centers O_i inside the hull we use the ∑_j 2/O_iO_j < π which we established in the first paragraph, where the sum has all n-1 terms. Thus we get ∑_i,j 2/O_iO_j < (n-2)π, where for vertices i for which O_i is a vertex of the convex hull the sum is only over n-2 values of j and excludes 2/O_iO_{max i} where O_{max i}denotes the furthest center from O_i.

Now for O_i a vertex of the convex hull we have that the sum over all j, ∑ 2/O_iO_j, is the sum Σ' over all but j = max i plus at most 1/(n-2) Σ'. In other words we must increase the sum by at most a factor (n-1)/(n-2) to include the missing term. For O_i not a vertex of the hull, obviously no increase is needed. Thus the full sum ∑_i,j 2/O_iO_j < (n-1)π. Hence ∑_i<j 1/O_iO_j < (n-1)π/4 as required.

43rd IMO 2002