IMO 2001/B2 solution

IMO 2001

Problem B2

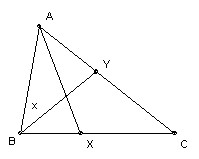
ABC is a triangle. X lies on BC and AX bisects angle A. Y lies on CA and BY bisects angle B. Angle A is 60^o. AB + BX = AY + YB. Find all possible values for angle B.

Answer

Answer: 80^o.

Solution

This is an inelegant solution, but I did get it fast! Without loss of generality we can take length AB = 1. Take angle ABY = x. Note that we can now solve the two triangles AXB and AYB. In particular, using the sine rule, BX = sin 30^o/sin(150^o-2x), AY = sin x/sin(120^o-x), YB = sin 60^o/sin(120^o-x). So we have an equation for x.

Using the usual formula for sin(a + b) etc, and writing s = sin x, c = cos x, we get: 2√3 s²c - 4sc - 2√3 c³ + 2√3 c² + 6sc - 2s - √3 = 0 or -√3 (4c³ - 2c² - 2c + 1) = 2s(2c² -3c + 1). This has a common factor 2c - 1. So c = 1/2 or -√3 (2c² - 1) = 2s(c - 1) (*).

c = 1/2 means x = 60^o or angle B = 120^o. But in that case the sides opposite A and B are parallel and the triangle is degenerate (a case we assume is disallowed). So squaring (*) and using s² = 1 - c², we get: 16c⁴ - 8c³ - 12c² + 8c - 1 = 0. This has another factor 2c - 1. Dividing that out we get: 8c³ - 6c + 1 = 0. But we remember that 4c³ - 3c = cos 3x, so we conclude that cos 3x = -1/2. That gives x = 40^o, 80^o, 160^o, 200^o, 280^o, 320^o. But we require that x < 60^o to avoid degeneracy. Hence the angle B = 2x = 80^o.

I subsequently found this geometric solution on the official Wolfram site (Wolfram was one of the sponsors of IMO 2001). I cannot say it is much easier, but at least it is geometric.

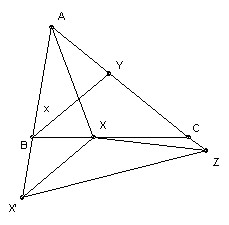
Extend AB to X' with BX' = BX. Extend AY to Z with YZ = YB. Then AZ = AY + YZ = AY + YB = AB + BX = AB + BX' = AX'. Angle A = 60^o, so AZX' is equilateral.

Use B also to denote the angle at B. Then angle YBX = B/2. Also angle BXX' + angle BX'X = B. The triangle is isosceles by construction, so angle BX'X = B/2. Hence angle XX'Z = 60^o - B/2. X lies on the bisector of A and AZ = AX', so XZ = XX'. Hence XZX' = 60^o - B/2 also. But angle Z = 60^o, so angle YZX = B/2 = angle YBX.

Now YZ = YB, so angle YZB = angle YBZ. Hence angle XZB = angle XBX (they are the difference of pairs of equal angles). If X does not lie on BZ, then we can conclude that XB = XZ.

In that case, since XZ = XX', we have XB = XX'. But already XB = BX' (by construction), so BXX' is equilateral and hence B/2 = 60^o. But then angle B + angle A = 180^o, so the triangle ABC is degenerate (with C at infinity), which we assume is disallowed. Hence X must lie on BZ, which means Z = C and angle B = 2 angle C. Hence angle B = 80, angle C = 40.

42nd IMO 2001